Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
"Многочлен и его стандартный вид"
Содержание
- 1. "Многочлен и его стандартный вид"
- 2. СИММЕТРИЯСимметрия –
- 3. Симметрия в природеВ растительном и животном мире можно увидеть различные виды симметрии
- 4. Симметрия в искусствеСимметрия – это та идея,
- 5. Симметрия в наукеГеометрическая симметрия –
- 6. Виды геометрических симметрий : Зеркальная
- 7. Зеркальная симметрияЗеркальная симметрия – тип симметрии объекта, когда объект при операции отражения переходит в себя
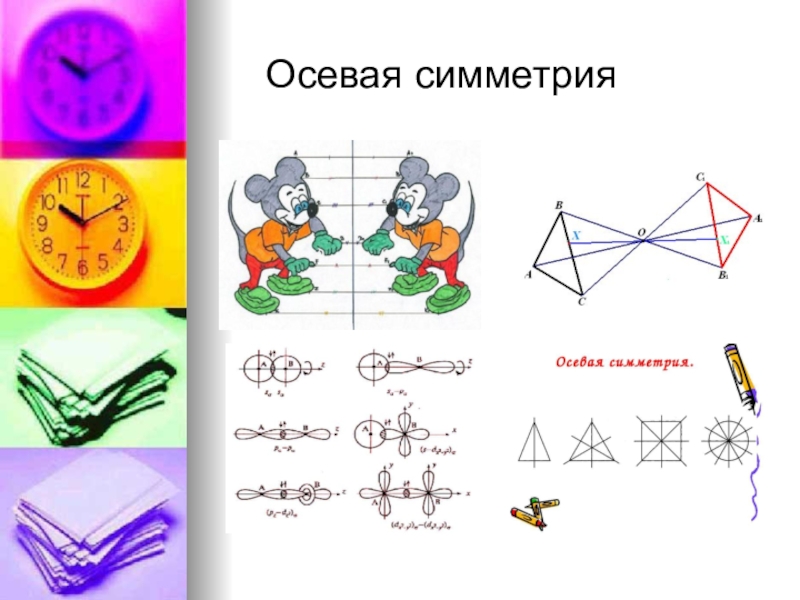
- 8. Осевая симметрия Осевая
- 9. Осевая симметрия Иногда также
- 10. Осевая симметрия
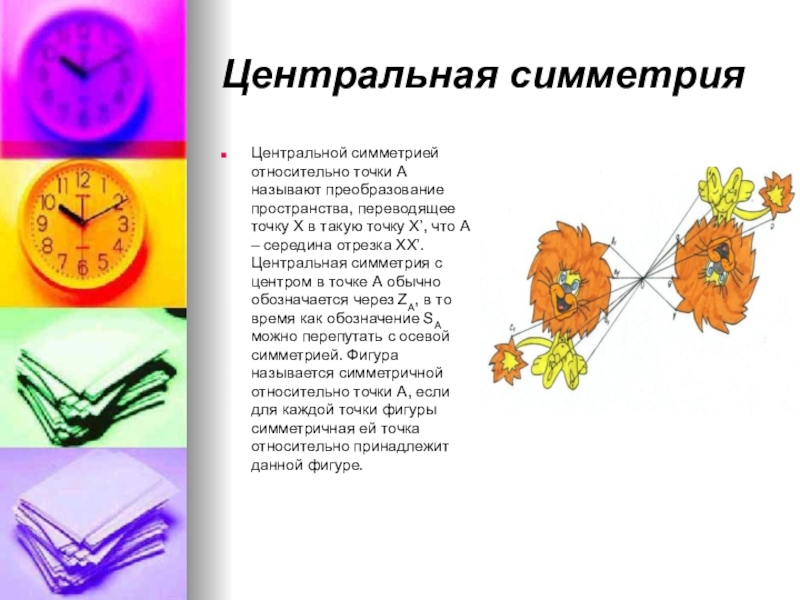
- 11. Центральная симметрияЦентральной симметрией относительно точки А называют
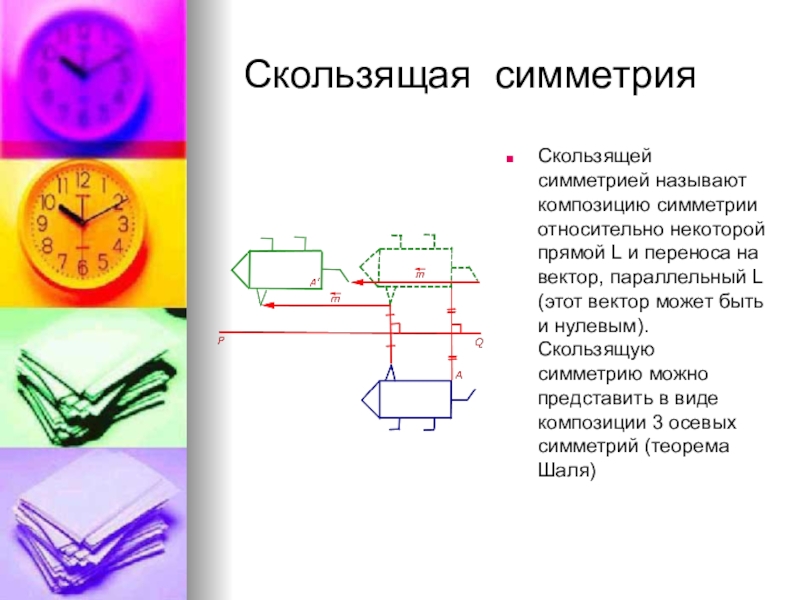
- 12. Скользящая симметрияСкользящей симметрией называют композицию симметрии
- 13. Скачать презентанцию
СИММЕТРИЯСимметрия – свойство геометрической фигуры, характеризующее некоторую правильность формы, неизменность её при действии и отражении. В древности слово симметрия употреблялось как «гармония» , «красота»
Слайды и текст этой презентации
Слайд 4Симметрия в искусстве
Симметрия – это та идея, которой человек на
протяжении столетий, пытался постичь и создать порядок, красоту, совершенство. Симметрия с
давних времён считался синонимом прекрасного. Симметрия, как объективный признак красоты, проходит через всю историю искусств.Слайд 5 Симметрия в науке
Геометрическая симметрия – это наиболее известный
тип для многих людей. Геометрический объект называется симметричным, если после
того как он был преобразован геометрически, он сохраняет некоторые исходные свойства.Слайд 6Виды геометрических симметрий :
Зеркальная симметрия;
Осевая симметрия;
Вращательная симметрия;
Центральная симметрия;
Скользящая симметрия;
Точечная симметрия;
Винтовая
симметрия. Слайд 7 Зеркальная симметрия
Зеркальная симметрия – тип симметрии объекта, когда объект
при операции отражения переходит в себя
Слайд 8 Осевая симметрия
Осевая симметрия – тип
симметрии, имеющий два несколько отличающихся определений:
Отражательная симметрия – вид
движения (зеркального отражения), при котором множеством неподвижных точек является прямая, называемая осью симметрии.В естественных науках под осевой симметрией понимают вращательную симметрию относительно поворотов вокруг прямой. При этом тело называют осесимметричными, если они переходят в себя при любом повороте вокруг этой прямой.
Слайд 9 Осевая симметрия
Иногда также вводят осевую симметрию
n-го порядка:
Осевая симметрия n-го порядка –симметричность относительно поворотов на угол
3600/n вокруг какой-либо оси.Зеркально-поворотная симметрия n-го порядка- симметричность относительно поворотов на угол 3600/n вокруг какой-либо оси.