Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Геометрическая фигура - треугольник
Содержание
- 1. Геометрическая фигура - треугольник
- 2. Треугольник — простейший многоугольник, имеющий 3 вершины (угла)
- 3. Обозначения Точки вершин треугольника традиционно обозначаются
- 4. Типы треугольников По величине
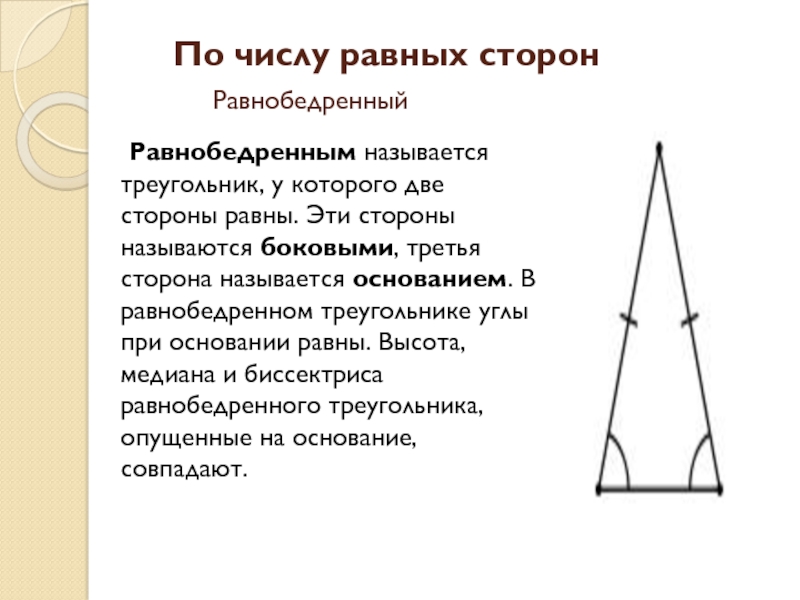
- 5. По числу равных сторон Равнобедренный Равнобедренным называется треугольник,
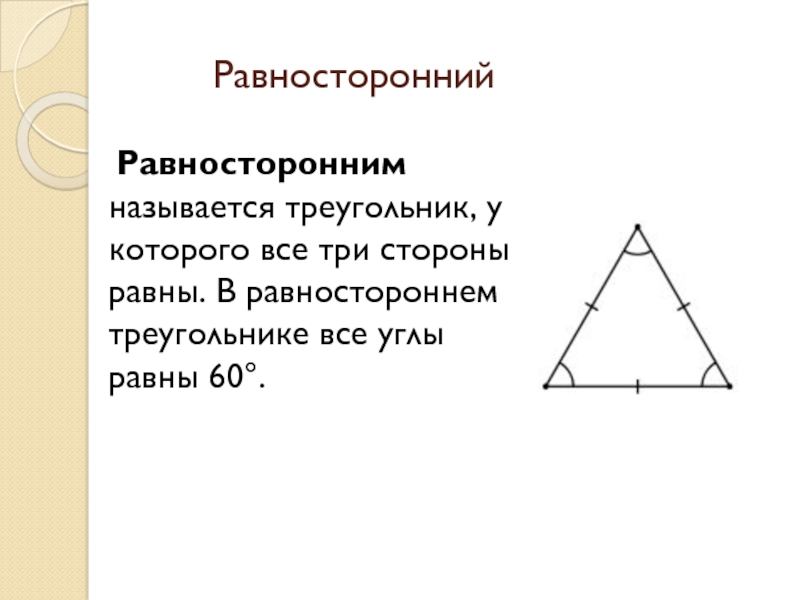
- 6. Равносторонний Равносторонним называется треугольник, у которого все
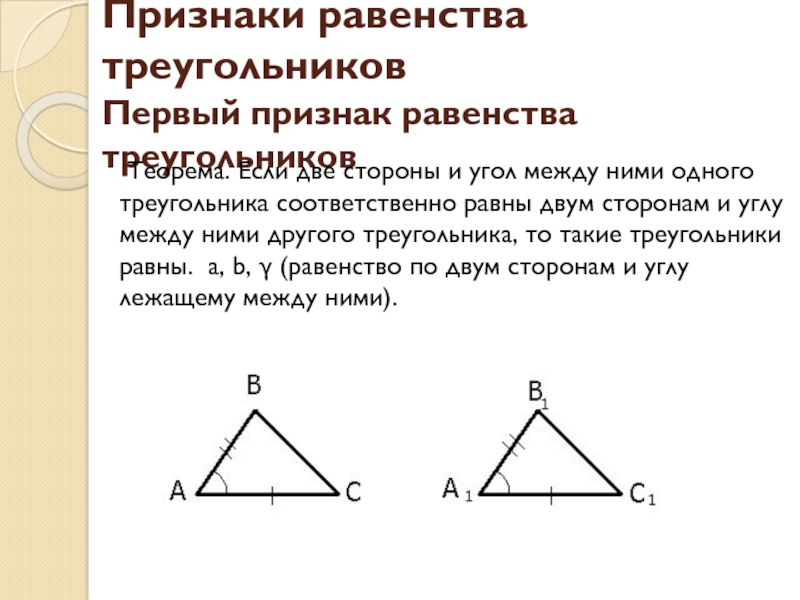
- 7. Признаки равенства треугольников Первый признак равенства треугольников Теорема.
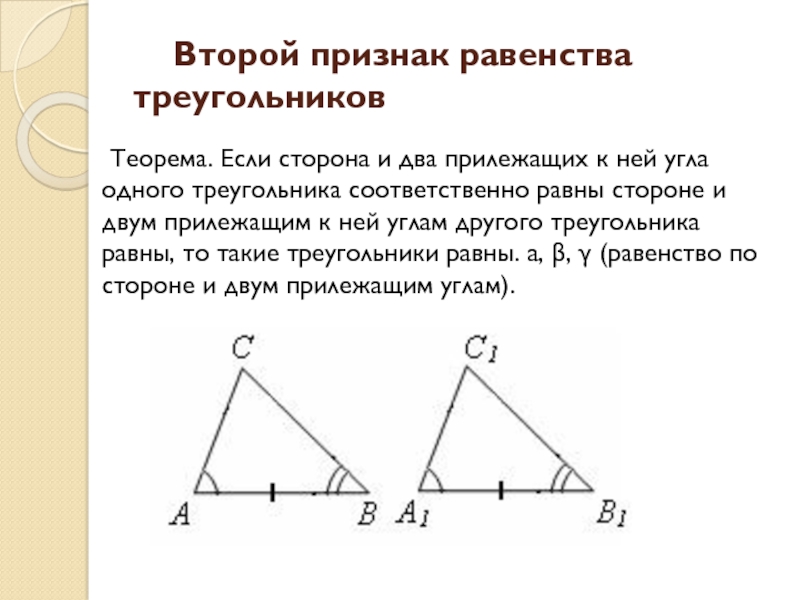
- 8. Второй признак равенства треугольников Теорема. Если сторона и
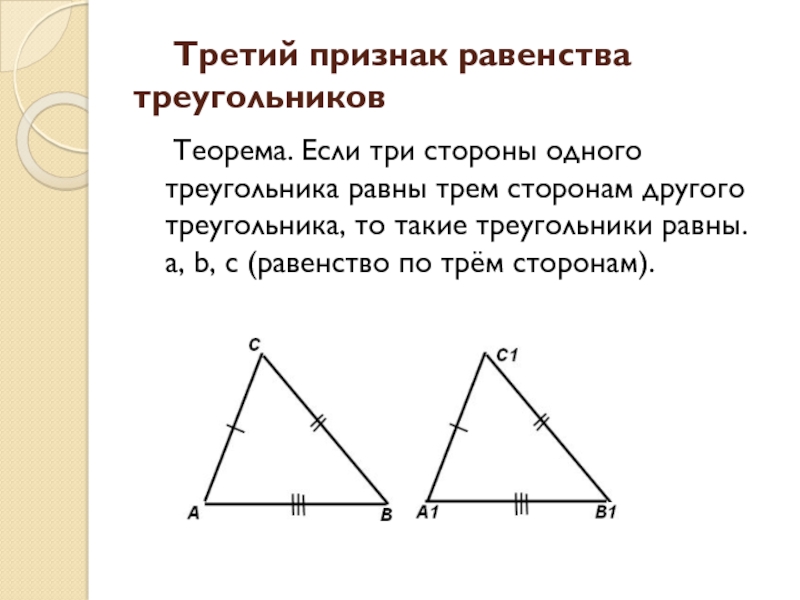
- 9. Третий признак равенства треугольников Теорема. Если три стороны
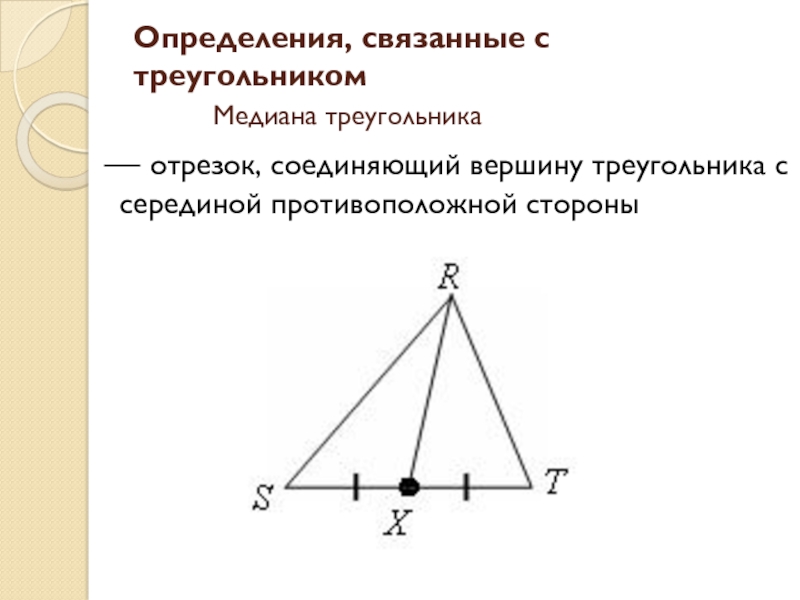
- 10. Определения, связанные с треугольником Медиана треугольника — отрезок, соединяющий вершину треугольника с серединой противоположной стороны
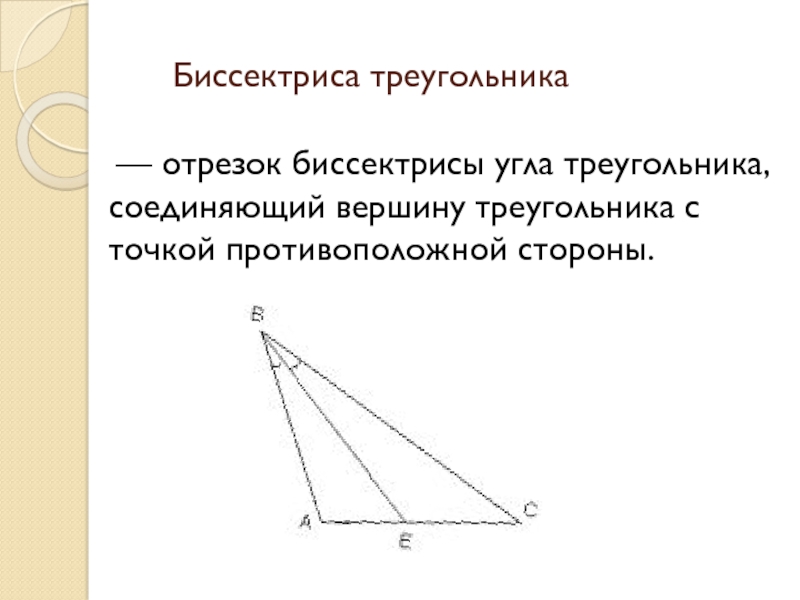
- 11. Биссектриса треугольника — отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны.
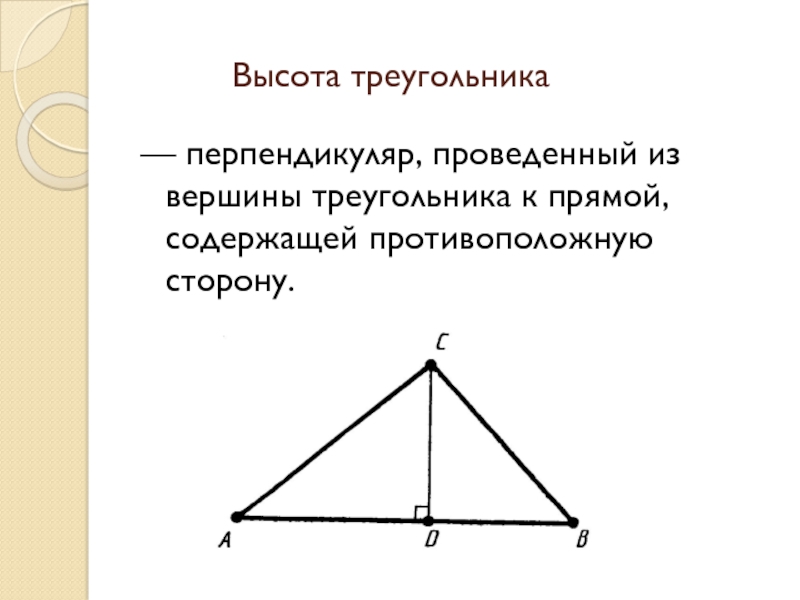
- 12. Высота треугольника — перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону.
- 13. Скачать презентанцию
Треугольник — простейший многоугольник, имеющий 3 вершины (угла) и 3 стороны; часть плоскости, ограниченная тремя точками, и тремя отрезками, попарно соединяющими эти точки.
Слайды и текст этой презентации
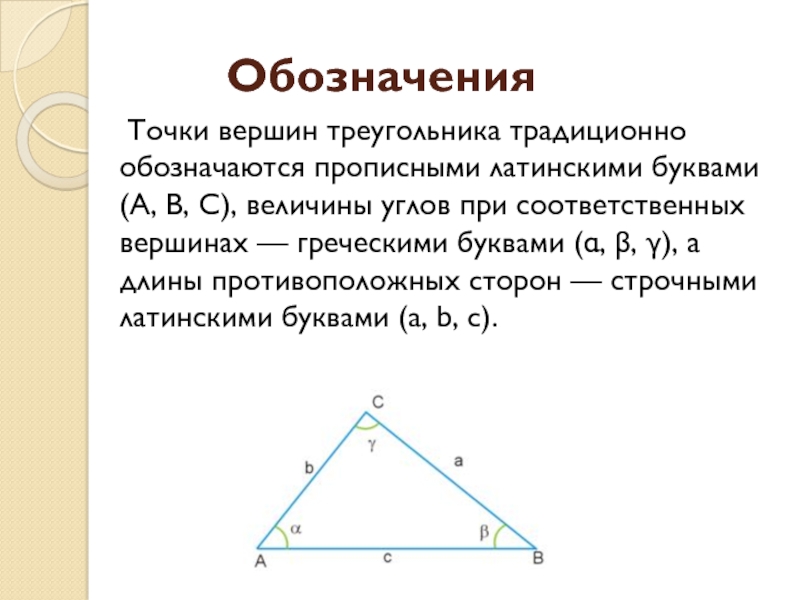
Слайд 3 Обозначения
Точки вершин треугольника традиционно обозначаются прописными латинскими буквами
(A, B, C), величины углов при соответственных вершинах — греческими буквами
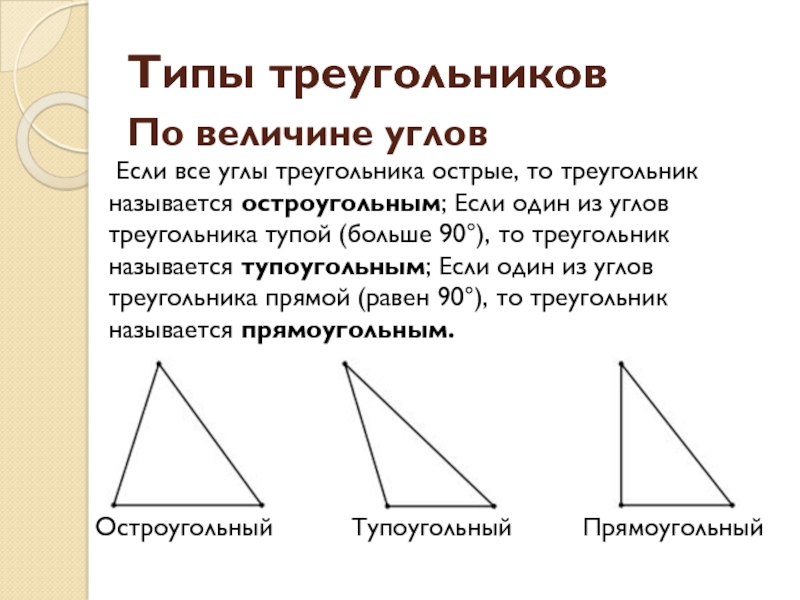
(α, β, γ), а длины противоположных сторон — строчными латинскими буквами (a, b, c).
Слайд 4 Типы треугольников
По величине углов
Если все углы треугольника
острые, то треугольник называется остроугольным; Если один из углов треугольника
тупой (больше 90°), то треугольник называется тупоугольным; Если один из углов треугольника прямой (равен 90°), то треугольник называется прямоугольным.Остроугольный
Тупоугольный
Прямоугольный
Слайд 5 По числу равных сторон
Равнобедренный
Равнобедренным называется треугольник, у которого две стороны
равны. Эти стороны называются боковыми, третья сторона называется основанием. В
равнобедренном треугольнике углы при основании равны. Высота, медиана и биссектриса равнобедренного треугольника, опущенные на основание, совпадают.
Слайд 6 Равносторонний
Равносторонним называется треугольник, у которого все три стороны равны.
В равностороннем треугольнике все углы равны 60°.
Слайд 7Признаки равенства треугольников
Первый признак равенства треугольников
Теорема. Если две стороны и
угол между ними одного треугольника соответственно равны двум сторонам и
углу между ними другого треугольника, то такие треугольники равны. a, b, γ (равенство по двум сторонам и углу лежащему между ними).
Слайд 8 Второй признак равенства треугольников
Теорема. Если сторона и два прилежащих к
ней угла одного треугольника соответственно равны стороне и двум прилежащим
к ней углам другого треугольника равны, то такие треугольники равны. a, β, γ (равенство по стороне и двум прилежащим углам).
Слайд 9 Третий признак равенства треугольников
Теорема. Если три стороны одного треугольника равны
трем сторонам другого треугольника, то такие треугольники равны. a, b,
c (равенство по трём сторонам).
Слайд 10Определения, связанные с треугольником
Медиана треугольника
— отрезок, соединяющий вершину треугольника
с серединой противоположной стороны
Слайд 11 Биссектриса треугольника
— отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с
точкой противоположной стороны.
Слайд 12 Высота треугольника
— перпендикуляр, проведенный из вершины
треугольника к прямой, содержащей противоположную сторону.
