Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Множества
Содержание
- 1. Множества
- 2. Понятие множества.Георг Кантор (1845-1918)Профессор математики и философии,
- 3. Понятие множества.Основное понятие в математике - понятие
- 4. Обозначение множестваМножества обозначаются заглавными буквами латинского алфавита:
- 5. Численность множестваЧисленность множества- число элементов в данном
- 6. Виды множеств:Дискретные множества(прерывные)- имеют отдельные элементы. Путём
- 7. Способы задания множеств Перечислением элементов (подходит для
- 8. ПодмножествоЕсли любой элемент множества В принадлежит множеству
- 9. Виды подмножествСобственное подмножество. Множество В называется собственным
- 10. АВА=ВРавенства множествМножества равны, если они состоят из
- 11. Операции над множествамиПересечение множеств.Объединение множеств.Разность множеств.Дополнение множества.
- 12. Объединение множествОбъединением множеств А и В называется
- 13. Пересечение множествПересечением множеств А и В называется
- 14. Разность множествРазностью множеств А и В называется
- 15. Дополнение множестваМножество элементов множества В, не принадлежащих
- 16. Свойства множествПересечение и объединение множеств обладают свойствами:КоммутативностьАссоциативностьДистрибутивность
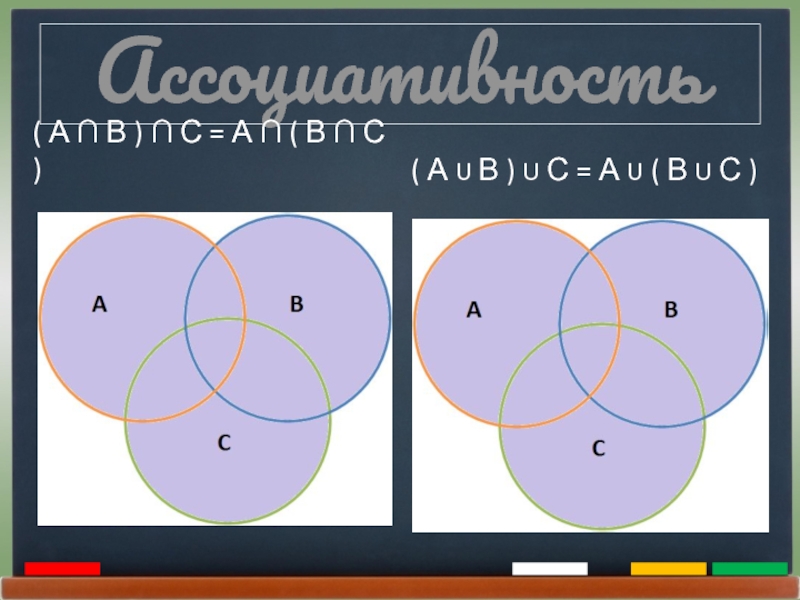
- 17. Ассоциативность( А ∩ В ) ∩ С
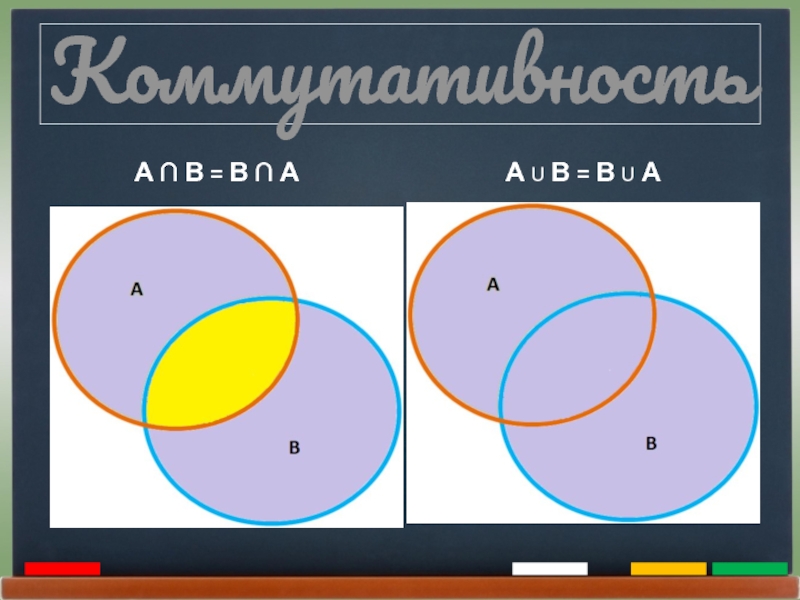
- 18. КоммутативностьА ∩ В = В ∩ АА U В = В U А
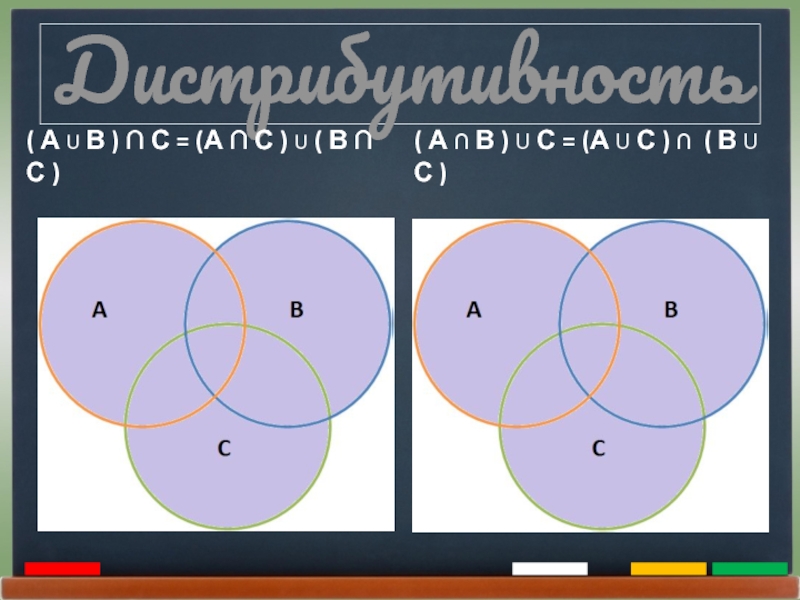
- 19. Дистрибутивность( А U В ) ∩ С
- 20. Отношения множествВ теории множеств рассматриваются отношения между
- 21. Свойства эквивалентностиОтношение эквивалентности обладает следующими свойствами:Симметричность(взаимность). Если
- 22. Скачать презентанцию
Понятие множества.Георг Кантор (1845-1918)Профессор математики и философии, основоположник современной теории множеств.«Под множеством мы подразумеваем объединение в целое определённых, различающихся между собой объектов нашего представления или мышления». Георг Кантор
Слайды и текст этой презентации
Слайд 2Понятие множества.
Георг Кантор (1845-1918)
Профессор математики и философии, основоположник современной теории
множеств.
собой объектов нашего представления или мышления». Георг КанторСлайд 3Понятие множества.
Основное понятие в математике - понятие множества.
Понятие множество
относится к первоначальным понятиям, не подлежащим определению.
Под множеством подразумевается
некоторая совокупность однородных объектов.Предметы ( объекты), составляющие множество, называются элементами.
Слайд 4Обозначение множества
Множества обозначаются заглавными буквами латинского алфавита: A, B, C,
X и др.
Элементы множества обозначаются строчными буквами латинского алфавита :
a, b, c, d и др.Запись M = { a , b, c, d } означает, что множество М состоит из элементов a , b, c, d.
Є – знак принадлежности. Запись а є М обозначает, что объект а является элементом множества М и читается так:
« а принадлежит множеству М »
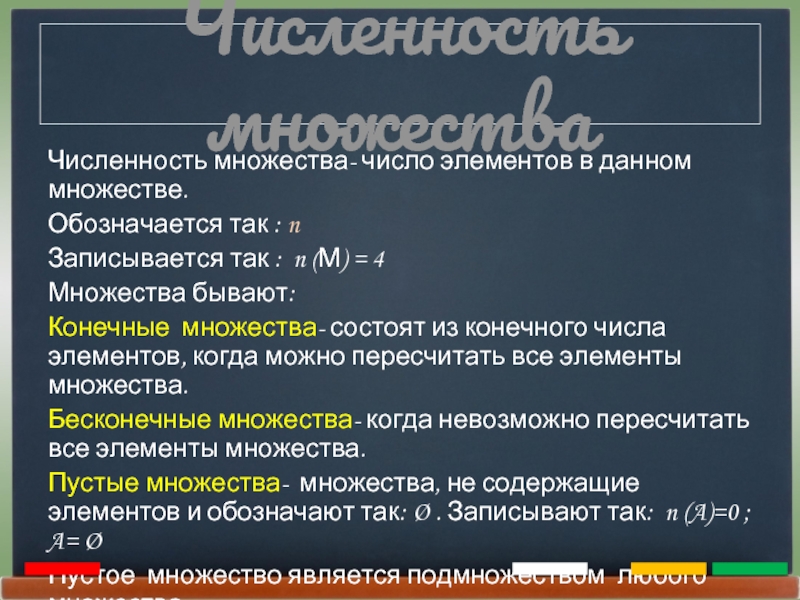
Слайд 5Численность множества
Численность множества- число элементов в данном множестве.
Обозначается так :
n
Записывается так : n (М) = 4
Множества бывают:
Конечные множества- состоят
из конечного числа элементов, когда можно пересчитать все элементы множества.Бесконечные множества- когда невозможно пересчитать все элементы множества.
Пустые множества- множества, не содержащие элементов и обозначают так: Ø . Записывают так: n (A)=0 ; A= Ø
Пустое множество является подмножеством любого множества.
Слайд 6Виды множеств:
Дискретные множества(прерывные)- имеют отдельные элементы. Путём счёта распознаются.
Непрерывные множества-
нет отдельных элементов. Распознаются путём измерения.
Конечные множества- состоят из конечного
числа элементов, когда можно пересчитать все элементы множества.Бесконечные множества- когда невозможно пересчитать все элементы множества.
Упорядочные множества. Элемент из множества предшествует или следует за другим. Множество натуральных чисел, расположенных в виде натурального ряда.
Неупорядочные множества. Любое неупорядочное множество можно упорядочить.
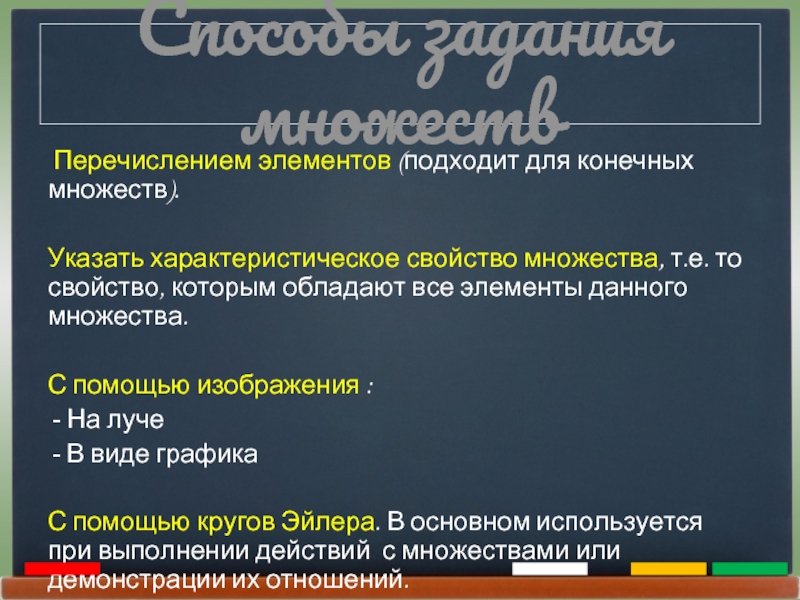
Слайд 7Способы задания множеств
Перечислением элементов (подходит для конечных множеств).
Указать характеристическое
свойство множества, т.е. то свойство, которым обладают все элементы данного
множества.С помощью изображения :
На луче
В виде графика
С помощью кругов Эйлера. В основном используется при выполнении действий с множествами или демонстрации их отношений.
Слайд 8Подмножество
Если любой элемент множества В принадлежит множеству А,
то множество
В называется подмножеством множества А.
- Знак включения.
Запись
В А означает, что множество В является подмножеством множества А.
Слайд 9Виды подмножеств
Собственное подмножество. Множество В называется собственным подмножеством множества А,
если выполняются условия: В≠Ø, В≠А.
Не собственные подмножества. Множество В называется
не собственным подмножеством множества А, если выполняются условия: В≠Ø, В=А.Пустое множество является подмножеством любого множества.
Любое множество является подмножеством самого себя.
Слайд 10А
В
А=В
Равенства множеств
Множества равны, если они состоят из одних и тех
же элементов.
Два множества являются равными , если каждый из них
является подмножеством другого.В этом случае пишут: А=В
Слайд 11Операции над множествами
Пересечение множеств.
Объединение множеств.
Разность множеств.
Дополнение множества.
Слайд 12Объединение множеств
Объединением множеств А и В называется множество всех объектов,
являющихся элементами множества А или множества В.
U- знак объединения.
А U
В читается так:«Объединение множества А и множества В».
Слайд 13Пересечение множеств
Пересечением множеств А и В называется множество, содержащее только
те элементы, которые одновременно принадлежат и множеству А и множеству
В.∩-знак пересечения, соответствует союзу «и».
А ∩ В читается так:
«Пересечение множеств А и В»
Слайд 14Разность множеств
Разностью множеств А и В называется множество всех объектов,
являющихся элементами множества А и не принадлежащих множеству В.
\ -
знак разности, соответствует предлогу «без».Разность множеств А и В записывается так: А \ В
Слайд 15Дополнение множества
Множество элементов множества В, не принадлежащих множеству А, называется
дополнением множества А до множества В.
Часто множества являются подмножествами некоторого
основного, или универсального множества U.Дополнение обозначается Ā
Слайд 16Свойства множеств
Пересечение и объединение множеств обладают свойствами:
Коммутативность
Ассоциативность
Дистрибутивность
Слайд 20Отношения множеств
В теории множеств рассматриваются отношения между множествами:
Тождественность. Если каждый
элемент множества А является также и элементом множества В ,
и каждый элемент множества В есть также элементом множества А, то эти множества тождественны. Обозначается так : А=В.Эквивалентность. Соответствие между элементами множеств А и В, при котором каждому элементу множества А соответствует единственный элемент множества В, и наоборот, различным элементам одного множества соответствуют различные элементы другого множества, называется взаимно однозначными. Если существует, по крайней мере, одно взаимно однозначное соответствие между элементами множеств А и В, то такие множества называются эквивалентными.
Слайд 21Свойства эквивалентности
Отношение эквивалентности обладает следующими свойствами:
Симметричность(взаимность). Если множество А эквивалентно
множеству В , то множество В эквивалентно множеству А.
А~В, В~А
Транзитивность
( переходность) . Если множество А эквивалентно множеству В , а множество В эквивалентно множеству С, то множества А и С эквивалентны.А~В, В~С, А~ С.
Рефлексивность ( возвратность). Всякое множество эквивалентно самому себе.
А~А
Использование отношения эквивалентности позволяет разбить всевозможные множества на классы эквивалентных между собой множеств.
Теги