Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Неполные квадратные уравнения
Содержание
- 1. Неполные квадратные уравнения
- 2. Математику нельзя изучать, наблюдая, как это делает сосед!А. Нивен
- 3. 1. Какое уравнение называется квадратным?2. Может ли
- 4. 3. Какое уравнение называется приведенным?4. Какое уравнение называют полным? Не полным?
- 5. 5. Укажите, какие из данных уравнений являются квадратными
- 6. ОтветыУравнение вида ax2+bx+c =0,
- 7. Слайд 7
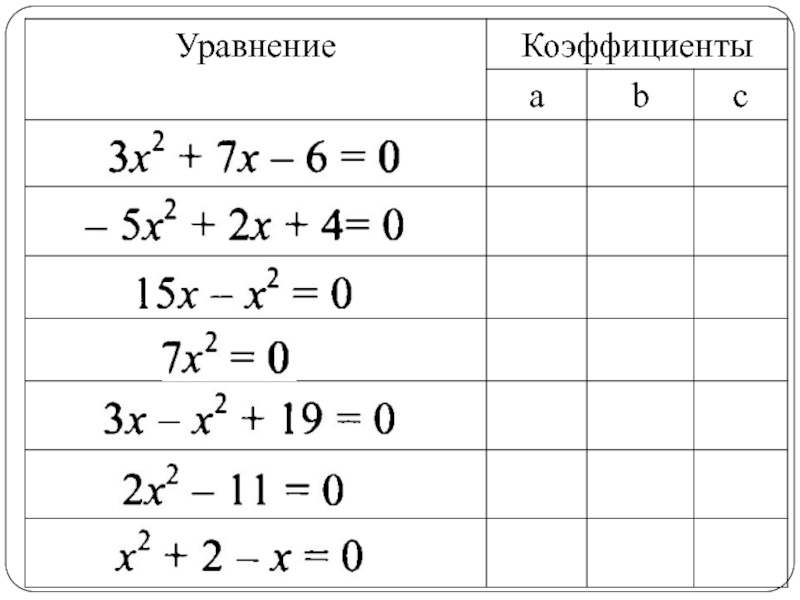
- 8. Составьте квадратное уравнение по его коэффициентам
- 9. Приведите уравнение к виду
- 10. Какие из данных уравнений являются приведенными? Не полными?
- 11. Решение неполных квадратных уравнений
- 12. 1. Уравнение вида ax2=0, где а≠0Пример1: 3,8x2=0Разделим
- 13. Вывод: Уравнение вида ax2=0 (а≠0) имеет единственный корень х=0.
- 14. 2. Уравнение вида ax2+с=0, где с≠0Пример2: -3х2+15=0Перенесем
- 15. Пример 3: 4х2+6=04х2+6=0,4х2=-6,х2=т.к. квадрат числа не может
- 16. Вывод: Для решения уравнений вида ax2+с=0 (с≠0)
- 17. 3. Уравнение вида ах2+bх=0, где b≠05х2+7х=0Разложим левую
- 18. Вывод: Для решения уравнений вида ax2+bx=0 (b≠0)
- 19. Таблица для неполных квадратных уравнений:
- 20. Работа по учебнику№ 519 (устно) № 518 № 523 (а, в)
- 21. Домашнее задание § 8, стр. 111-113 №
- 22. Желаю удачи в изучении алгебры!
- 23. Скачать презентанцию
Математику нельзя изучать, наблюдая, как это делает сосед!А. Нивен
Слайды и текст этой презентации
Слайд 31. Какое уравнение называется квадратным?
2. Может ли коэффициент а в
квадратном уравнении быть равным 0?
Слайд 6Ответы
Уравнение вида ax2+bx+c =0,
где а,
b, c –числа, а ≠0
Нет
Уравнение вида x2+bx+c =0, (a = 1)
Полным
– Если b и с ≠ 0Не полным – Если b или c = 0, или оба коэффициента равны нулю
а, в
Слайд 121. Уравнение вида ax2=0, где а≠0
Пример1: 3,8x2=0
Разделим обе части уравнения
на 3,8:
x2=0
т.к. существует только одно число 0,
квадрат которого равен 0, уравнение имеет единственный корень: х=0.Ответ: х=0.
Слайд 142. Уравнение вида ax2+с=0, где с≠0
Пример2: -3х2+15=0
Перенесем свободный член уравнения
в правую часть
Разделим обе части уравнения на -3
-3х2=-15,
х2=5.
Отсюда:
Ответ:
Слайд 15Пример 3: 4х2+6=0
4х2+6=0,
4х2=-6,
х2=
т.к. квадрат числа не может быть отрицательным числом,
то уравнение не имеет корней.
Ответ: нет корней.
Слайд 16Вывод:
Для решения уравнений вида ax2+с=0 (с≠0) воспользуемся алгоритмом:
Перенесем свободный
член с в правую часть уравнения.
Делим обе части уравнения на
а (с≠0), получаем уравнение: х2= ±
Если >0, то уравнение имеет два корня:
Если <0, то уравнение не имеет корней.
Слайд 173. Уравнение вида ах2+bх=0, где b≠0
5х2+7х=0
Разложим левую часть уравнения на
множители:
х(5х+7)=0
х=0 или 5х+7=0
5х=-7х=
х= -1,4
Ответ: х1=0, х2=-1,4
Слайд 18Вывод:
Для решения уравнений вида ax2+bx=0 (b≠0) воспользуемся алгоритмом:
Разложим левую
часть уравнения на множители, получим x(ax+b)=0
Решаем уравнение ax+b=0, x=
Уравнение имеет
два корня: x1=0, x2=