Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Определенный интеграл и его свойства
Содержание
- 1. Определенный интеграл и его свойства
- 2. ПервообразнаяФункция F(x) называется первообразной для функции f(x)
- 3. Неопределенный интегралСовокупность всех первообразных данной функции f(x)
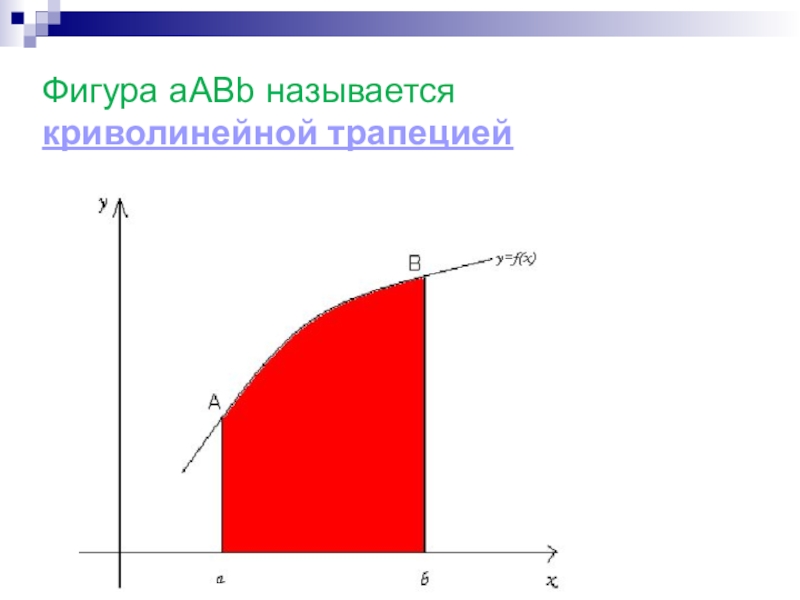
- 4. Фигура aABb называется криволинейной трапецией
- 5. Определенный интегралВычислим площадь криволинейной трапеции. Разобьем отрезок
- 6. Теорема: Если функция
- 7. Вычислите определённые интегралы:591
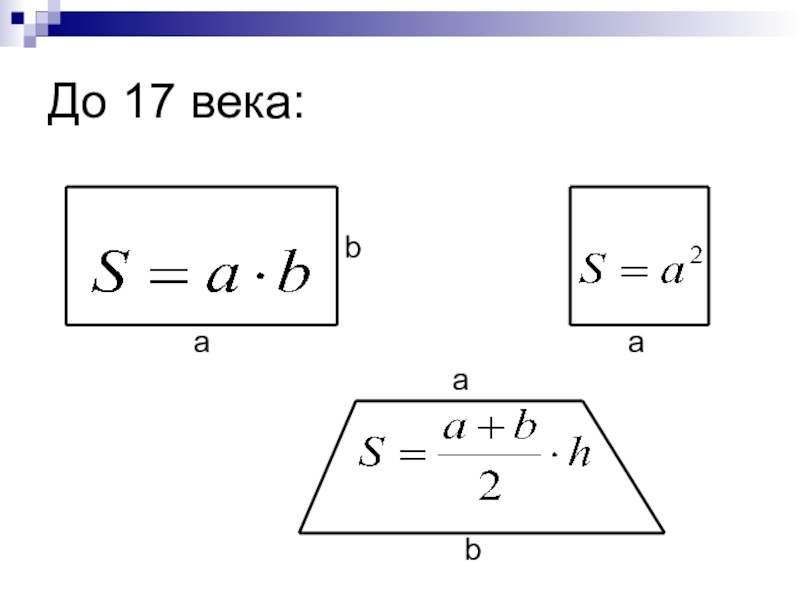
- 8. До 17 века:abaab
- 9. 0xyС появлением дифференциального и интегрального исчисления:SS
- 10. Историческая справка: Обозначение интеграла Лейбниц произвёл
- 11. Обозначение неопределённого интеграла ввёл Эйлер.Оформление определённого интеграла в привычном нам виде придумал Фурье.
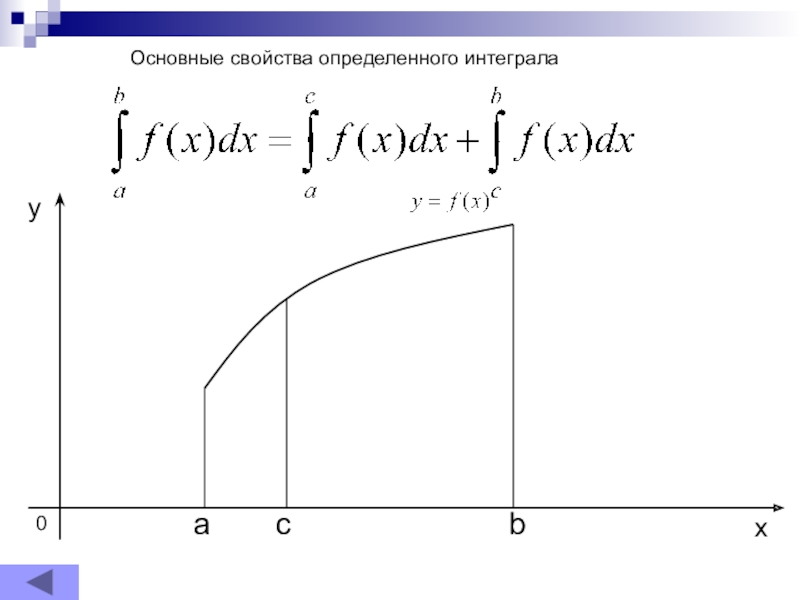
- 12. Основные свойства определенного интеграла
- 13. abx0сyОсновные свойства определенного интеграла
- 14. Основные свойства определенного интеграла
- 15. Слайд 15
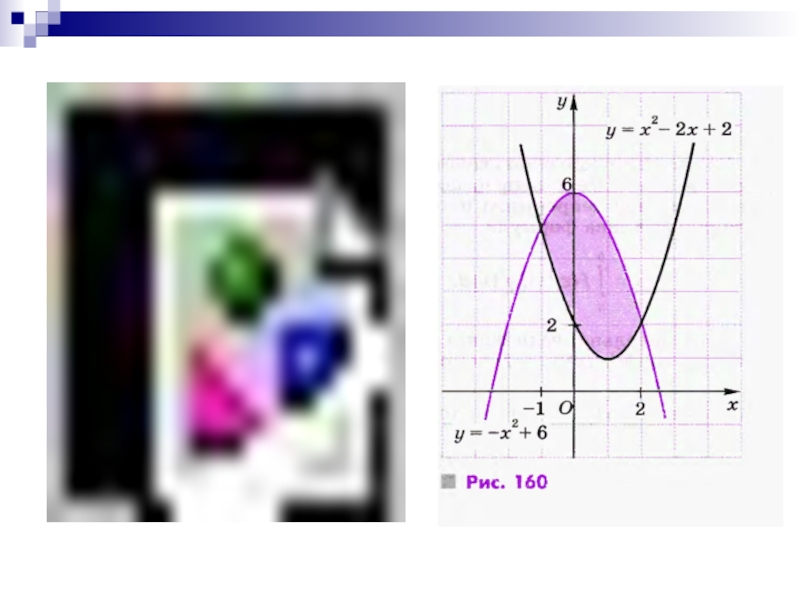
- 16. Площадь фигуры,Ограниченной графиками непрерывных функций y=f(x) и
- 17. Примеры Вычислить площадь фигуры, ограниченной линиями
- 18. Продолжение
- 19. Найти площадь фигуры ограниченной линиями
- 20. Подведение итоговДомашнее заданиеП.6.7 № 6.64(б,г,д),6.65(в), 6.69
- 21. СПАСИБО ЗА ВНИМАНИЕ!« ТАЛАНТ – это 99% труда и 1% способности» народная мудрость
- 22. Скачать презентанцию
ПервообразнаяФункция F(x) называется первообразной для функции f(x) на данном промежутке, если для любого x из этого промежутка F’(x) = f(x).Пример: Первообразной для функции f(x)=x на всей числовой оси является F(x)=x2/2, поскольку (x2/2)’=x.
Слайды и текст этой презентации
Слайд 2Первообразная
Функция F(x) называется первообразной для функции f(x) на данном промежутке,
если для любого x из этого промежутка F’(x) = f(x).
Пример:
Первообразной
для функции f(x)=x на всей числовой оси является F(x)=x2/2, поскольку (x2/2)’=x.
Слайд 3Неопределенный интеграл
Совокупность всех первообразных данной функции f(x) называется ее неопределенным
интегралом и обозначается :
, где C – произвольная постоянная.
Слайд 5Определенный интеграл
Вычислим площадь криволинейной трапеции. Разобьем отрезок [a;b] на n
равных частей. Проведем через полученные точки прямые, параллельные оси OY.
Заданная криволинейная трапеция разобьется на n частей. Площадь всей трапеции приближенно равна сумме площадей столбиков.по определению , его называют
определенным интегралом от функции
y=f(x) по отрезку [a;b] и обозначают так:
![Определенный интегралВычислим площадь криволинейной трапеции. Разобьем отрезок [a;b] на n равных частей. Проведем через полученные точки прямые,](/img/thumbs/c092deaa2810f2e9e454732feee76fec-800x.jpg "Определенный интеграл и его свойства Определенный интегралВычислим площадь криволинейной трапеции. Разобьем отрезок [a;b] на n равных")
Слайд 6Теорема: Если функция непрерывна на
отрезке [a,
b], а функцияявляется первообразной для
на этом отрезке, то справедлива
формула:
(3)
формула Ньютона-Лейбница
Слайд 10Историческая справка:
Обозначение интеграла Лейбниц произвёл от первой буквы
слова «Сумма» (Summa). Ньютон в своих работах не предложил альтернативной
символики интеграла, хотя пробовал различные варианты. Сам термин интеграл придумал Якоб Бернулли.Summa
Слайд 11 Обозначение неопределённого интеграла ввёл Эйлер.
Оформление определённого интеграла в привычном
нам виде придумал Фурье.
Слайд 16Площадь фигуры,
Ограниченной графиками непрерывных функций y=f(x) и y=g(x) таких, что
для
любого x из [a;b], где a и b – абсциссы
точек пересечения графиков функций:![Площадь фигуры,Ограниченной графиками непрерывных функций y=f(x) и y=g(x) таких, что для любого x из [a;b], где a и](/img/thumbs/b9d93e1da5cdcae0a9d3e09be0578c5a-800x.jpg "Определенный интеграл и его свойства Площадь фигуры,Ограниченной графиками непрерывных функций y=f(x) и y=g(x) таких, что для любого")
