Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Параллельность
Содержание
- 1. Параллельность
- 2. Параллельные прямые
- 3. Определение.Две прямые называются параллельными, если они не пересекаются.аbаIIb
- 4. Слайд 4
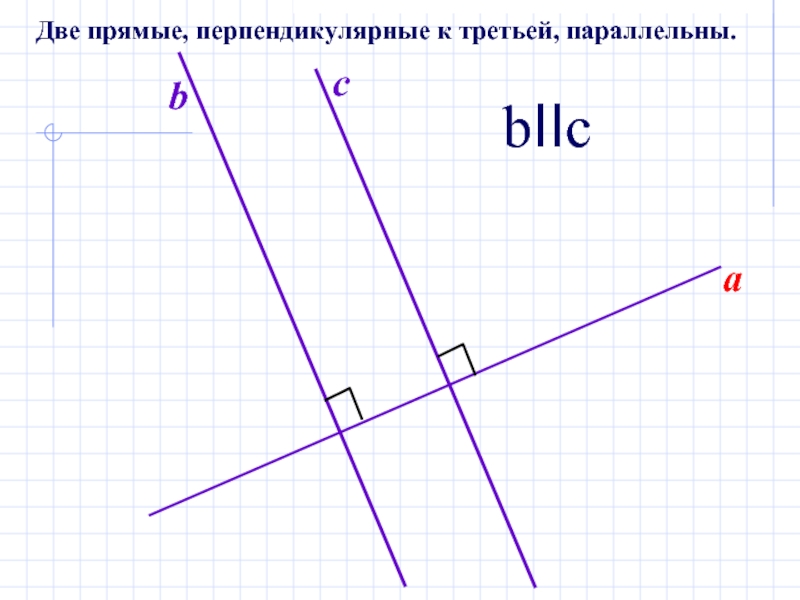
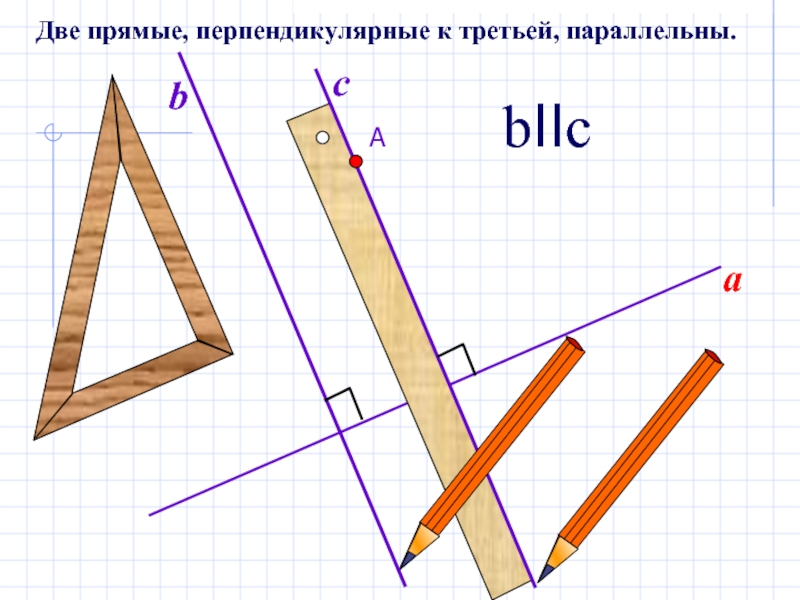
- 5. abcbIIcДве прямые, перпендикулярные к третьей, параллельны.
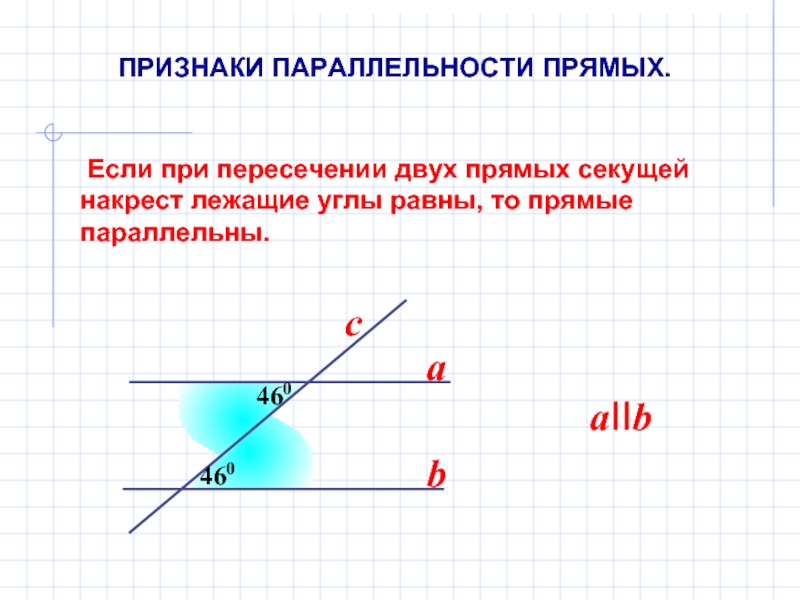
- 6. Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.460460abaIIbcПРИЗНАКИ ПАРАЛЛЕЛЬНОСТИ ПРЯМЫХ.
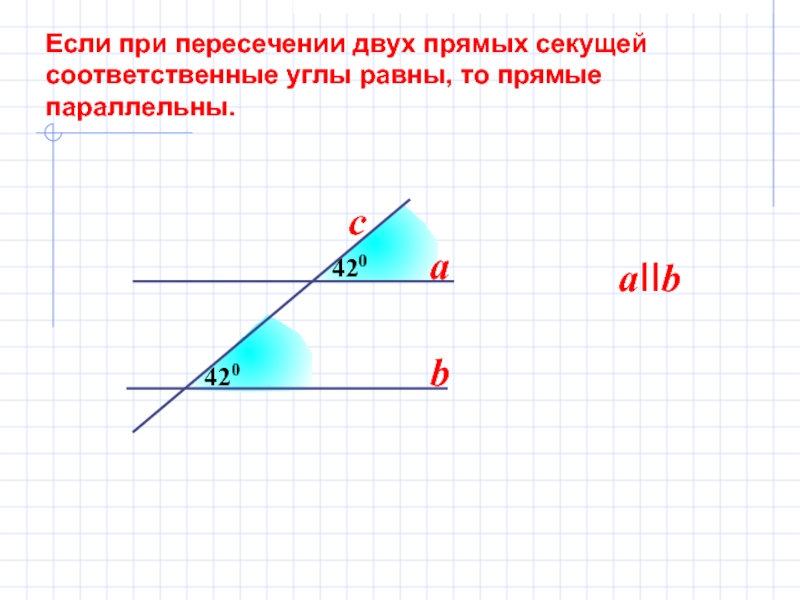
- 7. 420 Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.420abaIIbc
- 8. Слайд 8
- 9. Если при пересечении двух прямых
- 10. Тренировочные упражнения Параллельны ли прямые a и b b a d c132465
- 11. АabcbIIcДве прямые, перпендикулярные к третьей, параллельны.
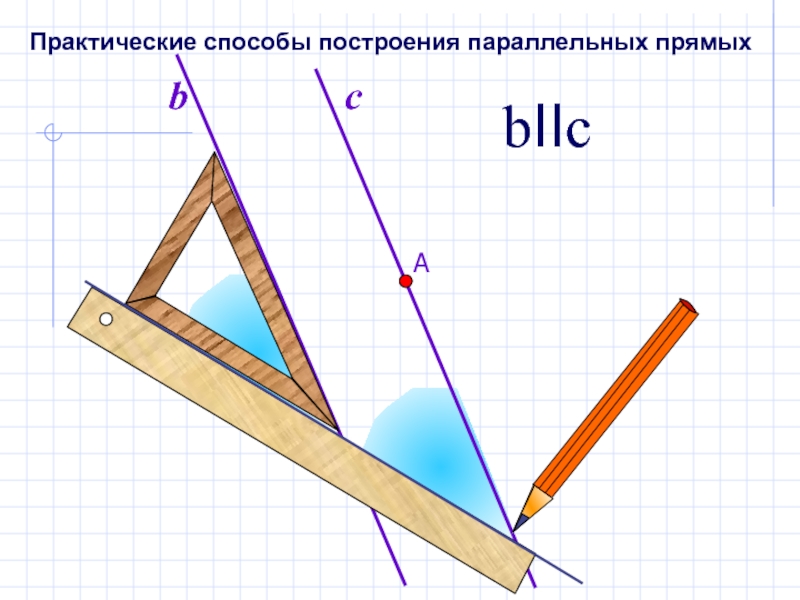
- 12. bbIIcПрактические способы построения параллельных прямых
- 13. Этим способом пользуются в чертежной практике.Способ построения
- 14. Параллельность прямой с плоскостью
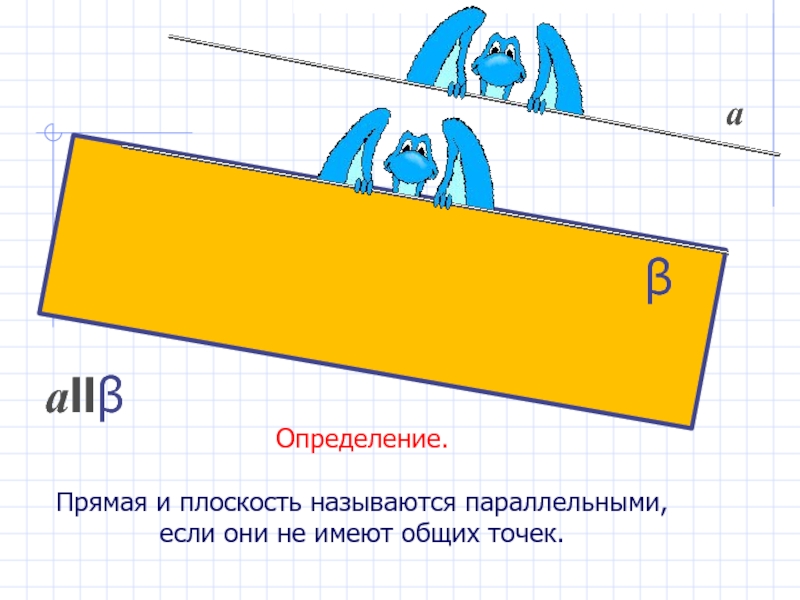
- 15. Определение.Прямая и плоскость называются параллельными, если они не имеют общих точек.аIIβаβ
- 16. Теорема.Если прямая, не лежащая в данной плоскости,
- 17. Слайд 17
- 18. Слайд 18
- 19. Параллельность плоскостей
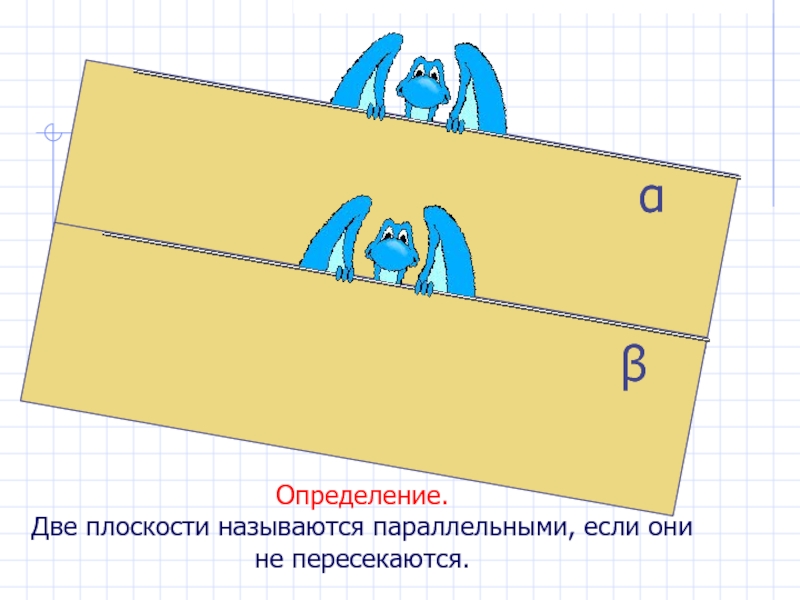
- 20. βαОпределение.Две плоскости называются параллельными, если они не пересекаются.
- 21. Теорема.Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.αβaba1b1α׀׀β
- 22. Свойства параллельных плоскостей
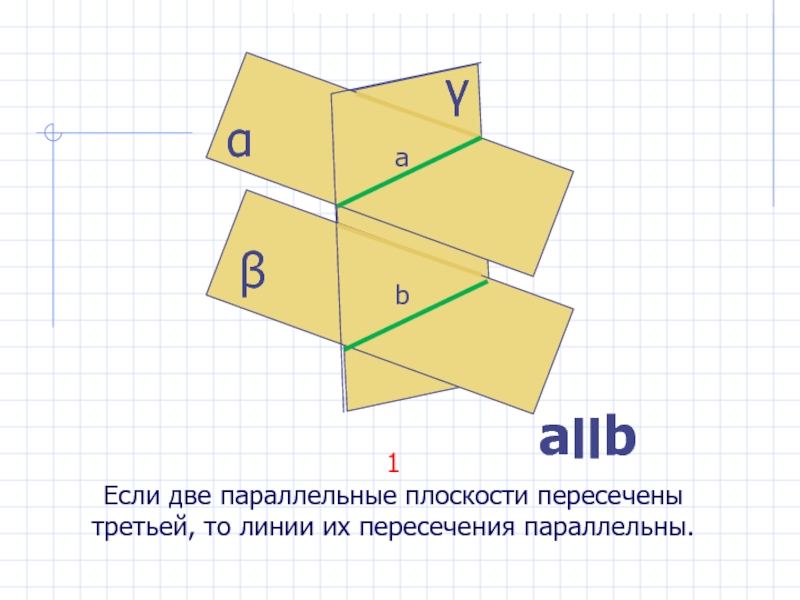
- 23. 1Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.αβγaba׀׀b
- 24. 2Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны.AB=CD
- 25. Скачать презентанцию
Параллельные прямые
Слайды и текст этой презентации
Слайд 1Носевич Сергей, Прялухин Евгений
Гапоненко Юлия 10 класс, учитель: Балинова Е.В.
Параллельность
Слайд 7
420
Если при пересечении двух прямых секущей
соответственные
углы равны, то прямые
параллельны.
420
a
b
aIIb
c
Слайд 8
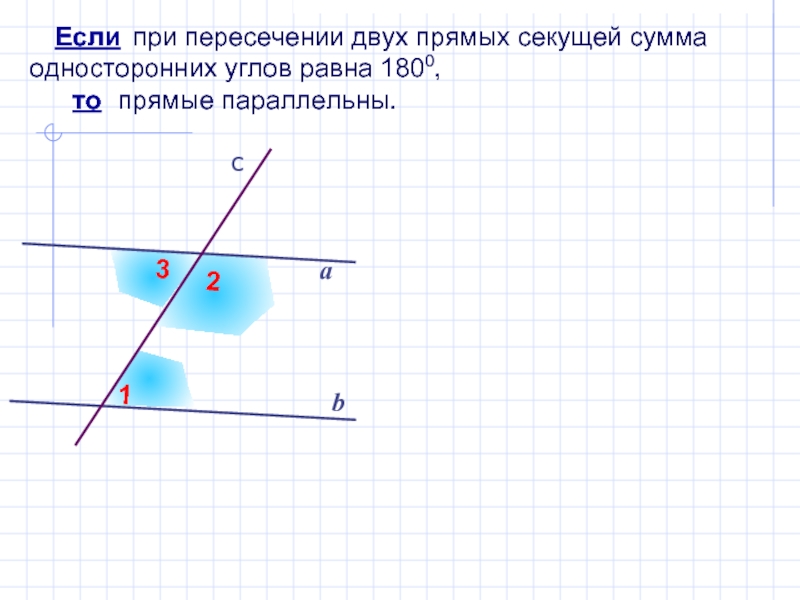
при пересечении двух
прямых секущей сумма односторонних углов равна 1800,
прямые параллельны.
b
а
Если
то
1
2
c
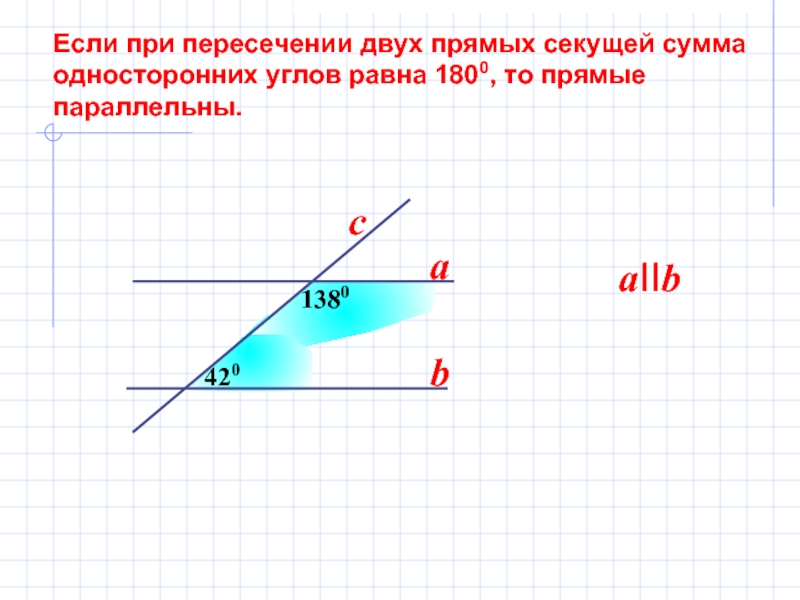
Слайд 9 Если при пересечении двух прямых секущей сумма
односторонних углов равна 1800, то прямые
параллельны.
420
1380
a
b
aIIb
c
Слайд 13
Этим способом пользуются в чертежной практике.
Способ построения параллельных прямых с
помощью
рейсшины.
Слайд 15Определение.
Прямая и плоскость называются параллельными, если они не имеют общих
точек.
аIIβ
а
β
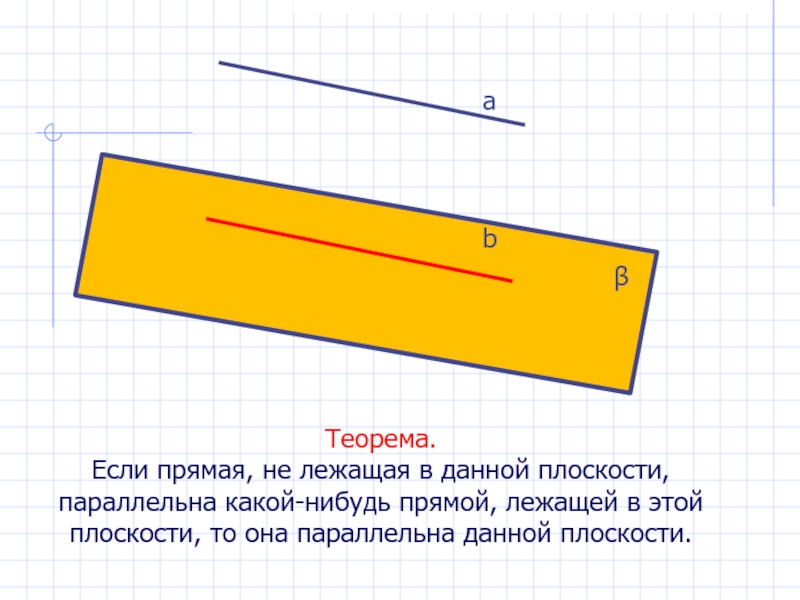
Слайд 16Теорема.
Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой,
лежащей в этой плоскости, то она параллельна данной плоскости.
a
b
β
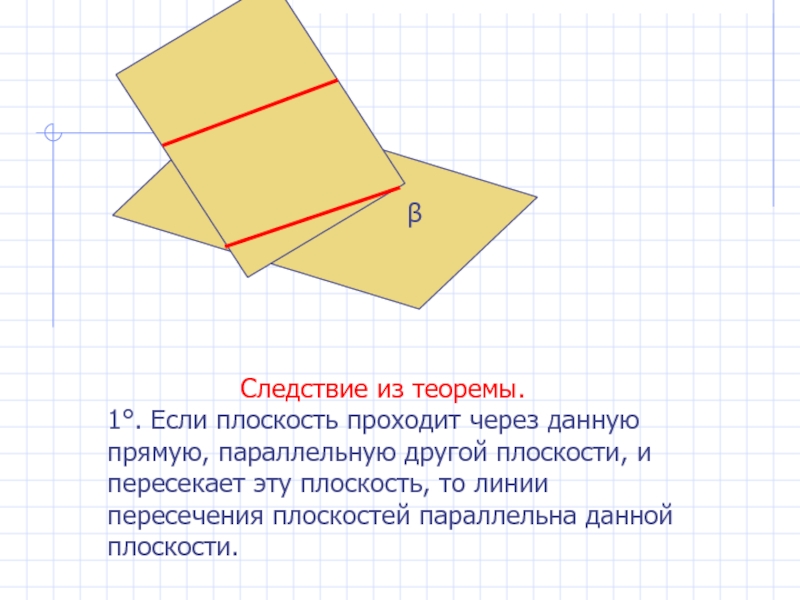
Слайд 17 Следствие из
теоремы.
1°. Если плоскость проходит через данную прямую, параллельную другой плоскости,
и пересекает эту плоскость, то линии пересечения плоскостей параллельна данной плоскости.β
Слайд 18 Следствие из теоремы.
2°.
Если одна из двух параллельных прямых параллельна данной плоскости, то
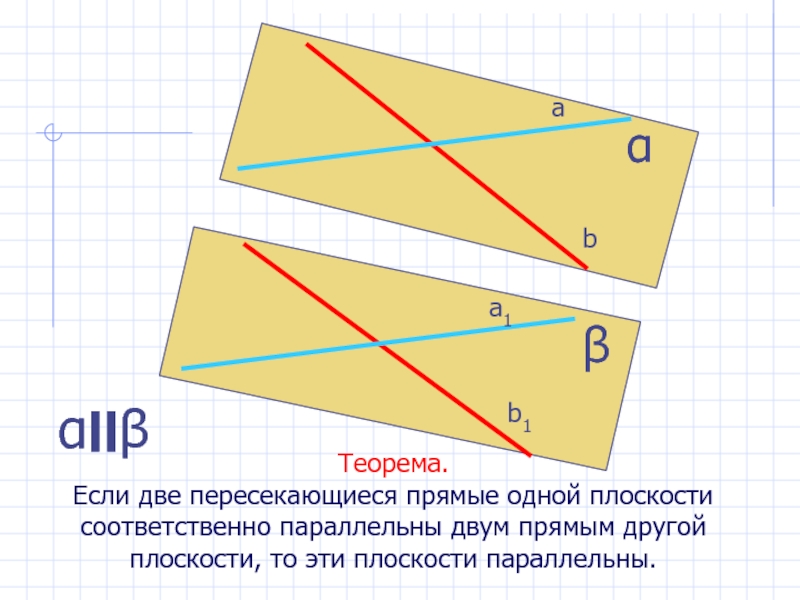
другая прямая либо также параллельна данной плоскости, либо лежит в этой плоскости.Слайд 21Теорема.
Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым
другой плоскости, то эти плоскости параллельны.
α
β
a
b
a1
b1
α׀׀β
Слайд 23
1
Если две параллельные плоскости пересечены третьей, то линии их пересечения
параллельны.
α
β
γ
a
b
a׀׀b
Теги