Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Параллельность в пространстве
Содержание
- 1. Параллельность в пространстве
- 2. ОглавлениеПараллельные прямые в пространстве.Параллельность трех прямых.Параллельность прямой и плоскости.Параллельность плоскостей.Свойства параллельных плоскостей.Кроссворд.
- 3. Параллельные прямые в пространстве Определение
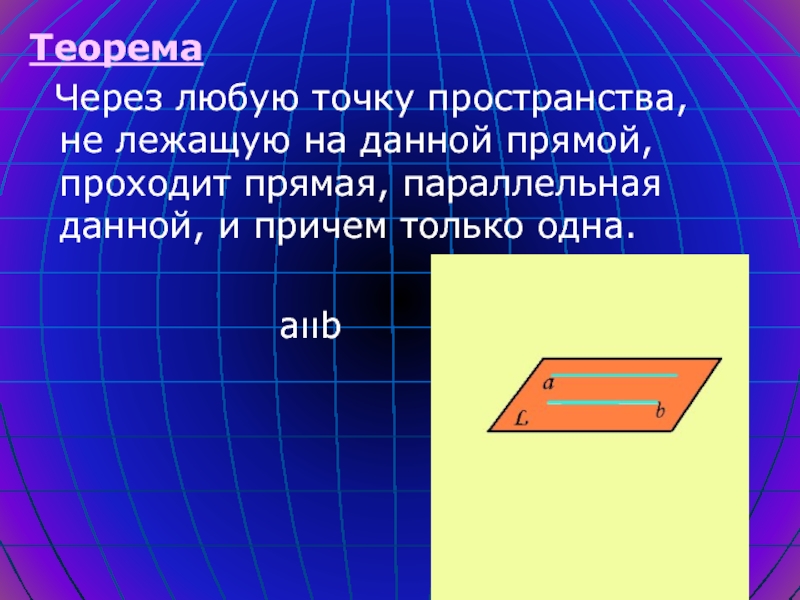
- 4. Теорема Через любую точку пространства, не лежащую
- 5. Теорема Если две прямые параллельны
- 6. Лемма Если одна из двух параллельных прямых
- 7. Параллельность прямой и плоскости Возможны три
- 8. Слайд 8
- 9. Слайд 9
- 10. ТеоремаЕсли прямая, не лежащая в данной плоскости,
- 11. Следствие Если плоскость проходит через данную прямую
- 12. СледствиеЕсли одна из двух параллельных прямых параллельна
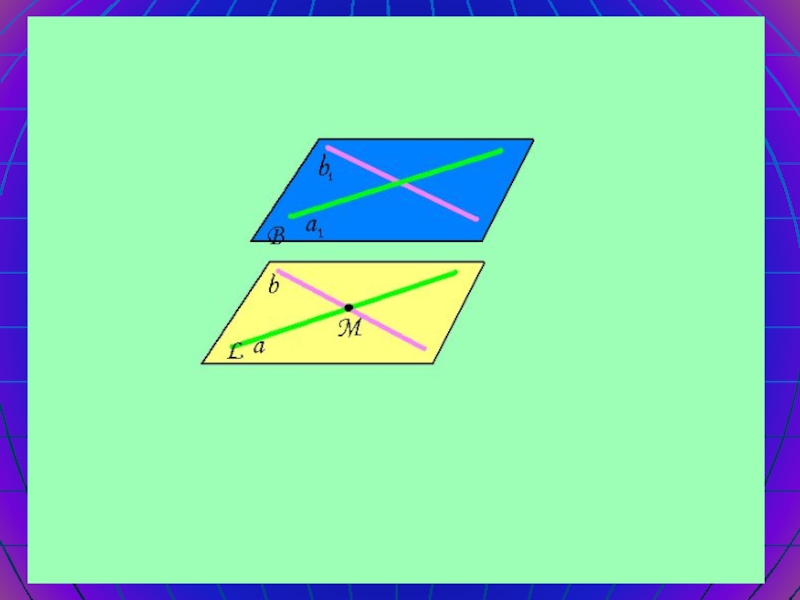
- 13. Параллельность плоскостей
- 14. Слайд 14
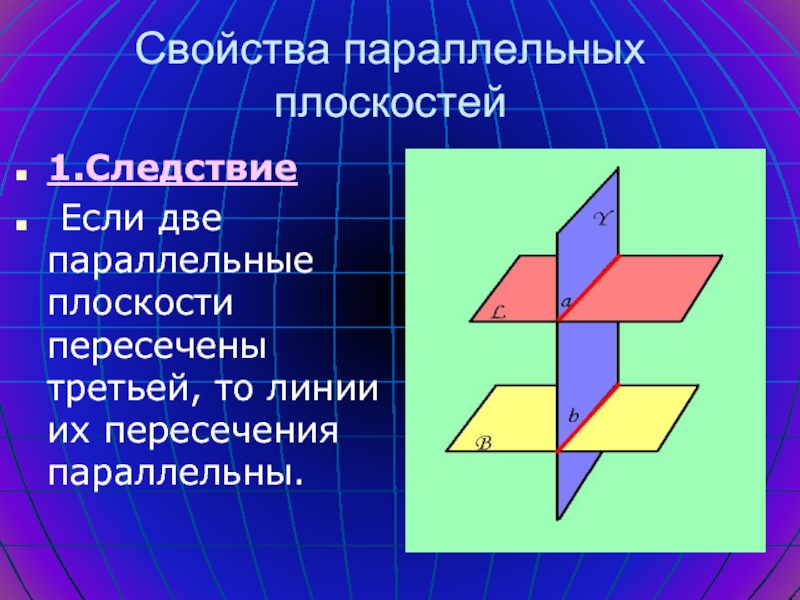
- 15. Свойства параллельных плоскостей1.Следствие Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.
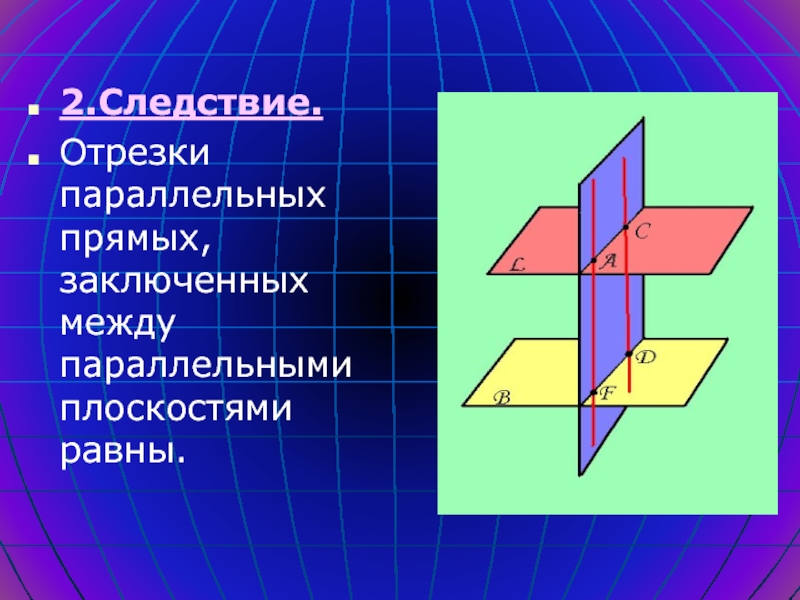
- 16. 2.Следствие.Отрезки параллельных прямых, заключенных между параллельными плоскостями равны.
- 17. Кроссворд
- 18. Скачать презентанцию
ОглавлениеПараллельные прямые в пространстве.Параллельность трех прямых.Параллельность прямой и плоскости.Параллельность плоскостей.Свойства параллельных плоскостей.Кроссворд.
Слайды и текст этой презентации
Слайд 2Оглавление
Параллельные прямые в пространстве.
Параллельность трех прямых.
Параллельность прямой и плоскости.
Параллельность плоскостей.
Свойства
параллельных плоскостей.
Слайд 3Параллельные прямые в пространстве
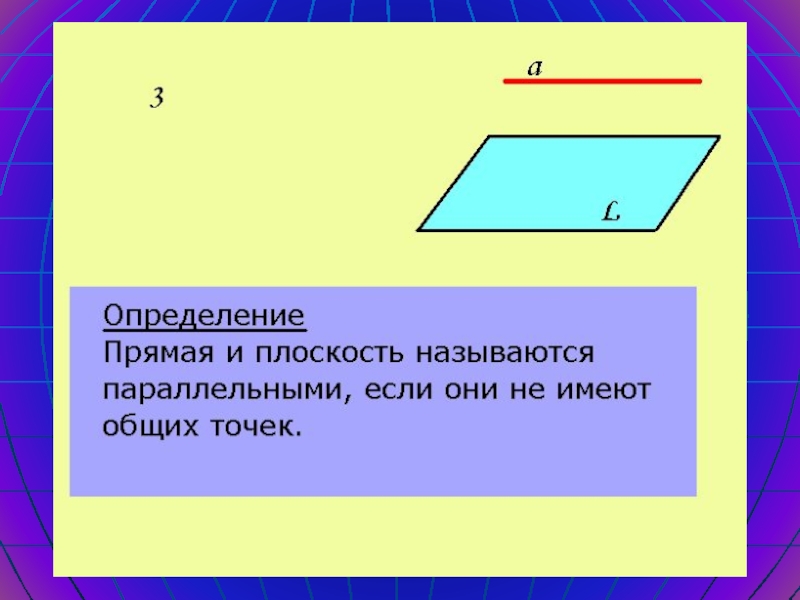
Определение
Две прямые в
пространстве называются параллельными, если они лежат в одной плоскости и
не пересекаются.Обозначение
а ιι b
с ιι d
Слайд 4Теорема
Через любую точку пространства, не лежащую на данной прямой,
проходит прямая, параллельная данной, и причем только одна.
аιιbСлайд 5 Теорема
Если две прямые параллельны третьей прямой, то
они параллельны.
bιιс аιιс
Значит
аιιb
Параллельность трех прямых
Слайд 6Лемма
Если одна из двух параллельных прямых пересекает данную плоскость,
то и другая прямая пересекает эту плоскость.
Значит
аιιb
Слайд 7Параллельность прямой и плоскости
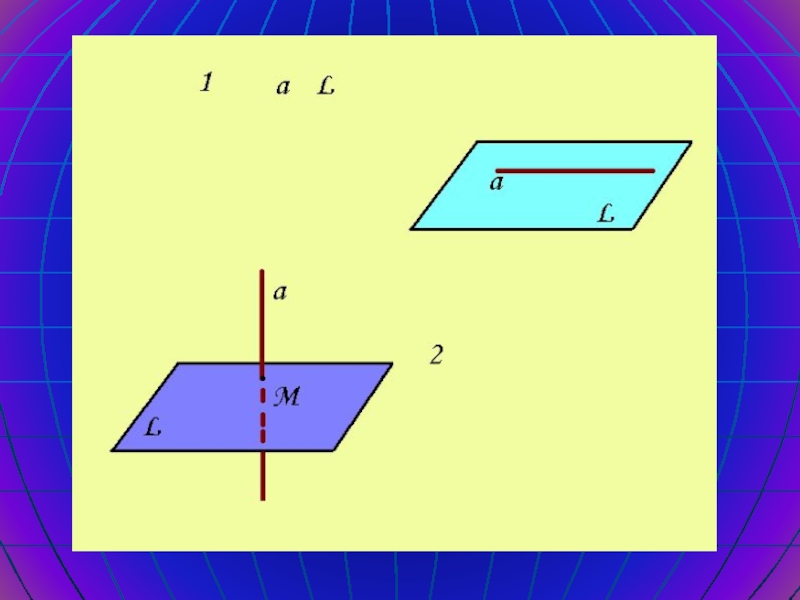
Возможны три случая взаимного расположения
прямой и плоскости в пространстве:
Прямая лежит в плоскости.
Прямая и плоскость
имеют только одну точку.Прямая и плоскость не имеют общих точек.
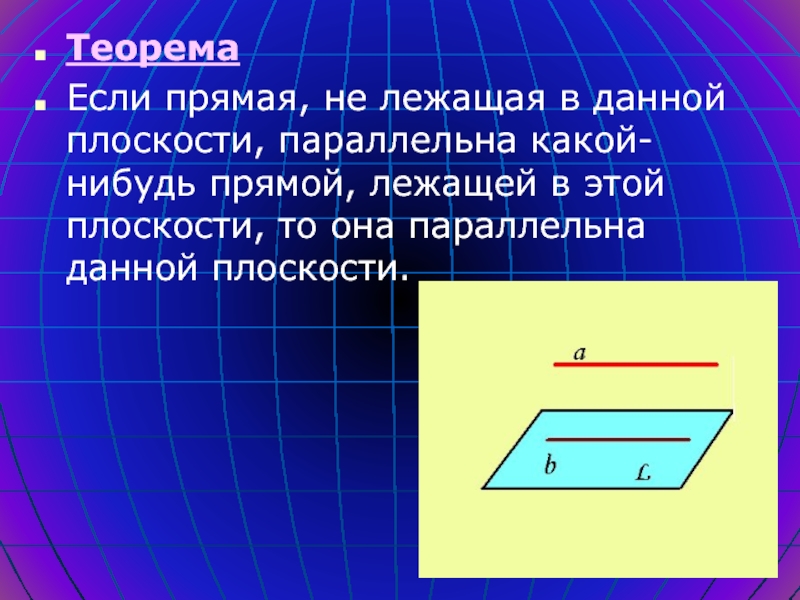
Слайд 10Теорема
Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой,
лежащей в этой плоскости, то она параллельна данной плоскости.
Слайд 11Следствие
Если плоскость проходит через данную прямую параллельную другой плоскости,
и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной
прямой.Слайд 12Следствие
Если одна из двух параллельных прямых параллельна данной плоскости, то
другая прямая либо также параллельна данной плоскости, либо лежит в
этой плоскости.Слайд 15Свойства параллельных плоскостей
1.Следствие
Если две параллельные плоскости пересечены третьей, то
линии их пересечения параллельны.
Теги