Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Перпендикулярность прямых в пространстве
Содержание
- 1. Перпендикулярность прямых в пространстве
- 2. ВСПОМНИМ ПЛАНИМЕТРИЮКаково может быть взаимное расположение двух прямых на плоскости?Какие прямые в планиметрии называются перпендикулярными?аавав
- 3. Взаимное расположение двух прямых в пространстве1.авсdmnkm
- 4. Признак перпендикулярности прямых в пространствеТеорема: Если две
- 5. ава1в1АВСА1А1С1В1αα11. α и α1 параллельны (по т.
- 6. ВЕРНЕМСЯ В ПРОСТРАНСТВОКаково может быть взаимное расположение
- 7. Какие прямые в пространстве называются перпендикулярными? АBCDА1B1C1D1AB
- 8. определениеПрямая, пересекающая плоскость, называется перпендикулярной этой плоскости,
- 9. Признак перпендикулярности прямой и плоскостиТ.17.2. Если прямая
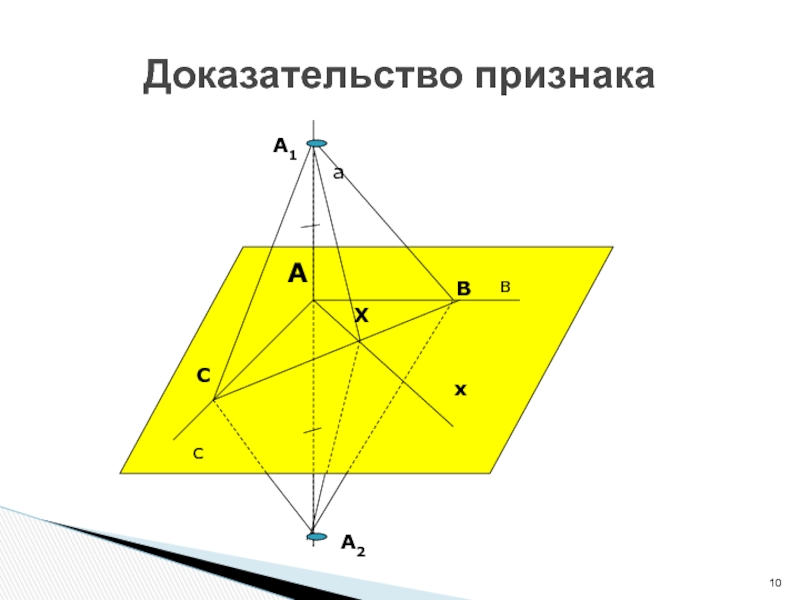
- 10. Доказательство признака всаАхВХСА2А1
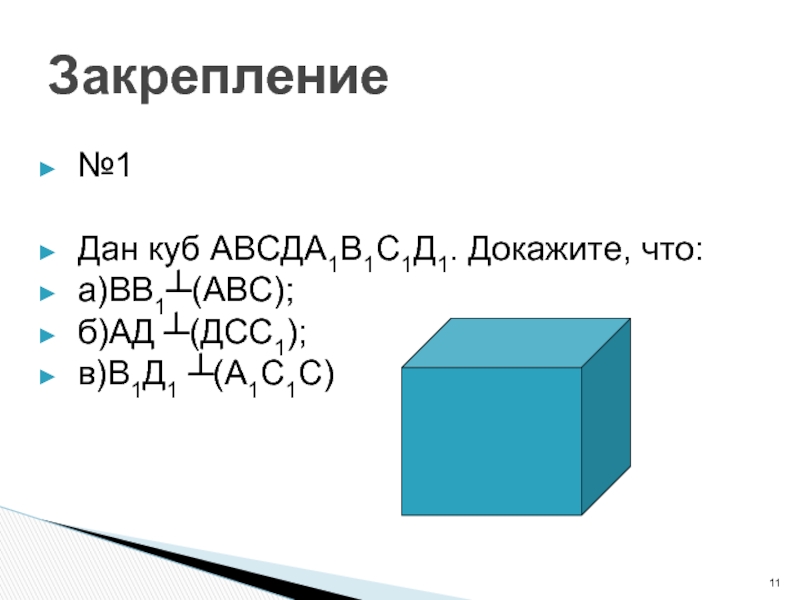
- 11. Закрепление№1Дан куб АВСДА1В1С1Д1. Докажите, что: а)ВВ1┴(АВС);б)АД ┴(ДСС1);в)В1Д1 ┴(А1С1С)
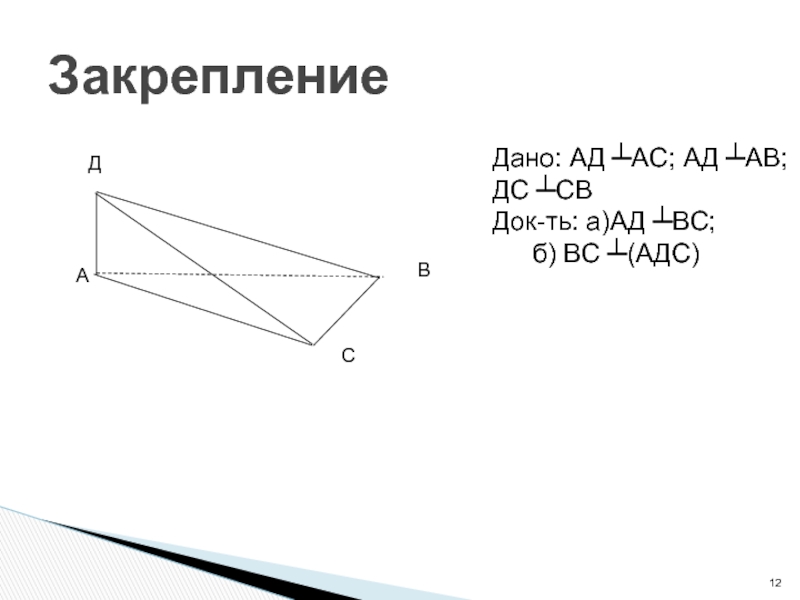
- 12. ЗакреплениеДАВСДано: АД ┴АС; АД ┴АВ;ДС ┴СВДок-ть: а)АД ┴ВС; б) ВС ┴(АДС)
- 13. Свойства перпендикулярных прямой и плоскостиТ.17.3х1а1а2х2
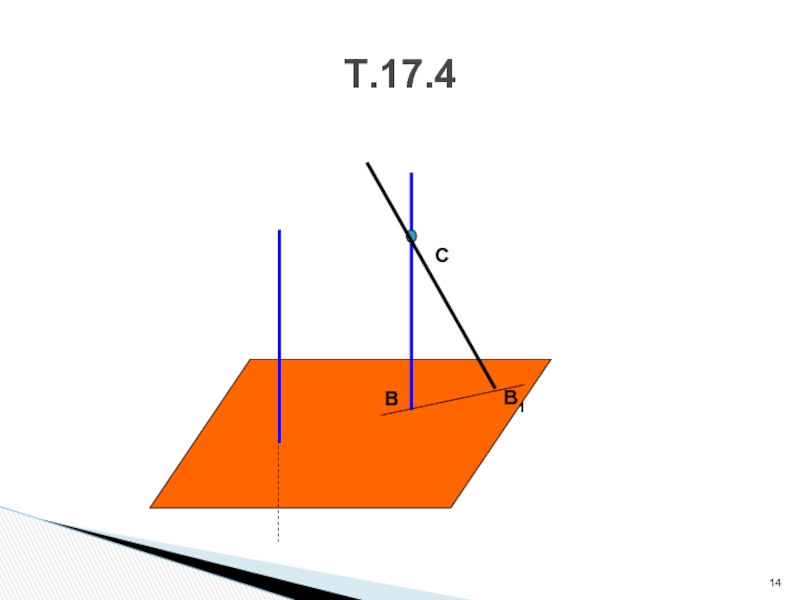
- 14. Т.17.4СВВ1
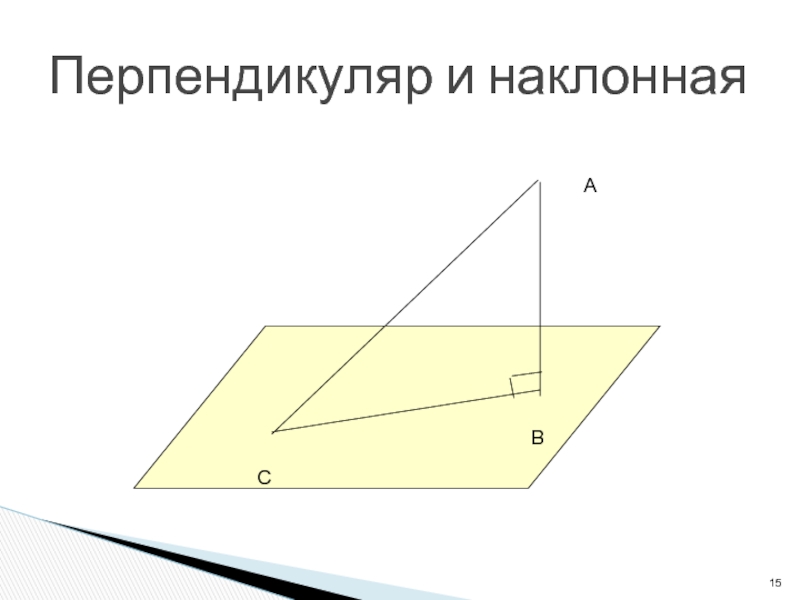
- 15. Перпендикуляр и наклоннаяАВС
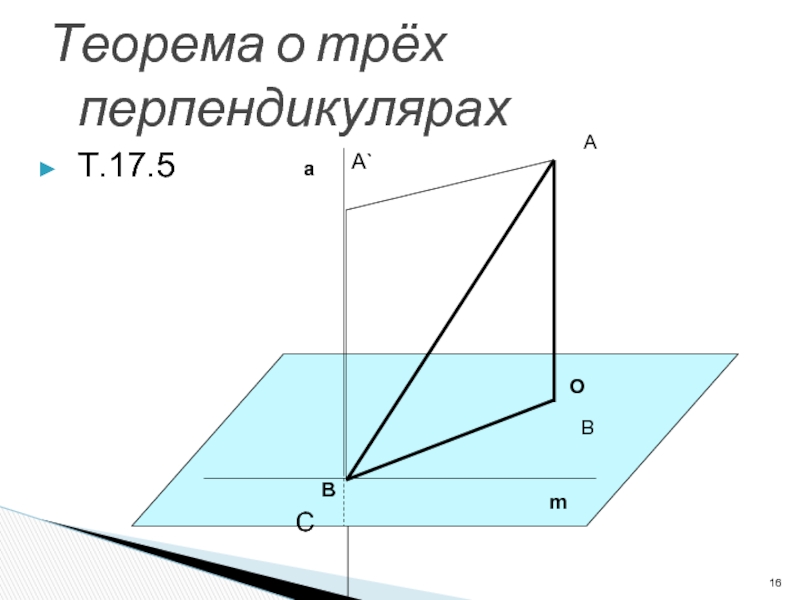
- 16. Теорема о трёх перпендикулярахТ.17.5СВАА`mОВа
- 17. Скачать презентанцию
ВСПОМНИМ ПЛАНИМЕТРИЮКаково может быть взаимное расположение двух прямых на плоскости?Какие прямые в планиметрии называются перпендикулярными?аавав
Слайды и текст этой презентации
Слайд 1Разработала
учитель математики
Гулова Р.И.
«Средняя общеобразовательная школа № 12 с
углубленным изучением
отдельных предметов» г. Старый Оскол
Слайд 2ВСПОМНИМ ПЛАНИМЕТРИЮ
Каково может быть взаимное расположение двух прямых на плоскости?
Какие
прямые в планиметрии называются перпендикулярными?
а
а
в
а
в
Слайд 4Признак перпендикулярности прямых в пространстве
Теорема:
Если две пересекающиеся прямые параллельны
соответственно двум перпендикулярным прямым, то они тоже перпендикулярны
Слайд 5а
в
а1
в1
А
В
С
А1
А1
С1
В1
α
α1
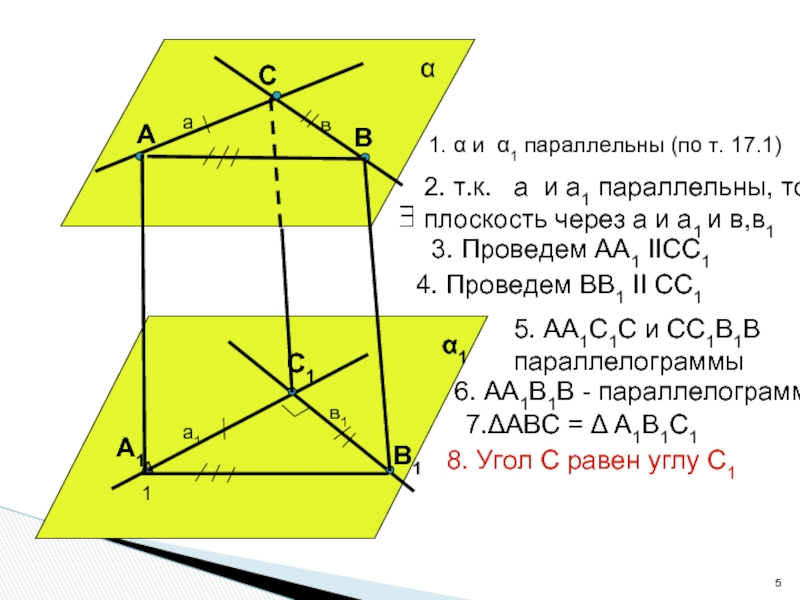
1. α и α1 параллельны (по т. 17.1)
2. т.к.
а и а1 параллельны, то
плоскость через а и а1
и в,в13. Проведем АА1 IICC1
4. Проведем ВВ1 II CC1
5. АА1С1С и СС1В1В
параллелограммы
6. АА1В1В - параллелограмм
7.ΔАВС = Δ А1В1С1
8. Угол С равен углу С1
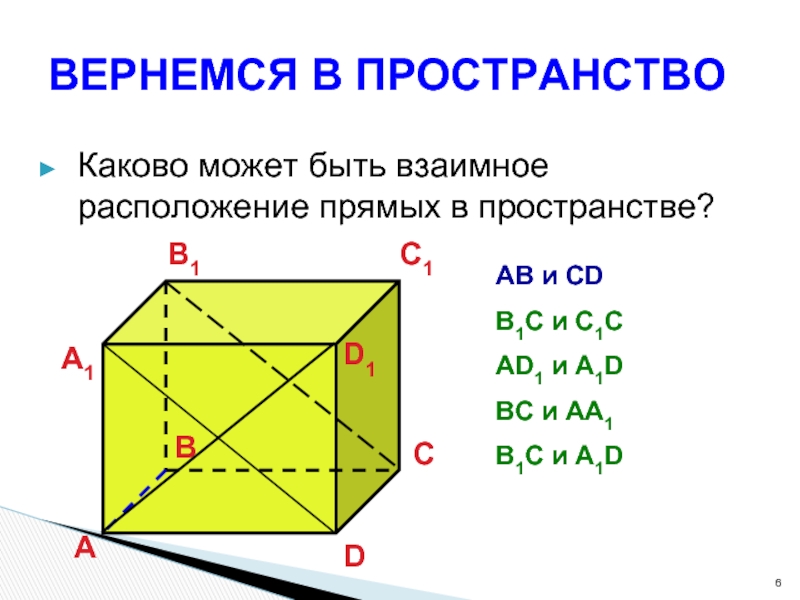
Слайд 6ВЕРНЕМСЯ В ПРОСТРАНСТВО
Каково может быть взаимное расположение прямых в пространстве?
А
B
C
D
А1
B1
C1
D1
AB
и CD
B1C и C1C
AD1 и A1D
BC и AA1
B1C и A1D
Слайд 7Какие прямые в пространстве называются перпендикулярными?
А
B
C
D
А1
B1
C1
D1
AB и CD
B1C и DC
AD1
и A1D
BC и AA1
B1C и A1D
Слайд 8определение
Прямая, пересекающая плоскость, называется перпендикулярной этой плоскости, если она перпендикулярна
любой прямой, лежащей в данной плоскости и проходит через точку
пересеченияСлайд 9Признак перпендикулярности прямой и плоскости
Т.17.2. Если прямая перпендикулярна двум пересекающимся
прямым, лежащим в плоскости, то она перпендикулярна и самой плоскости
Теги