Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Первый признак подобия треугольников
Содержание
- 1. Первый признак подобия треугольников
- 2. Цель:Повторить определение подобных треугольников, теорему об отношении
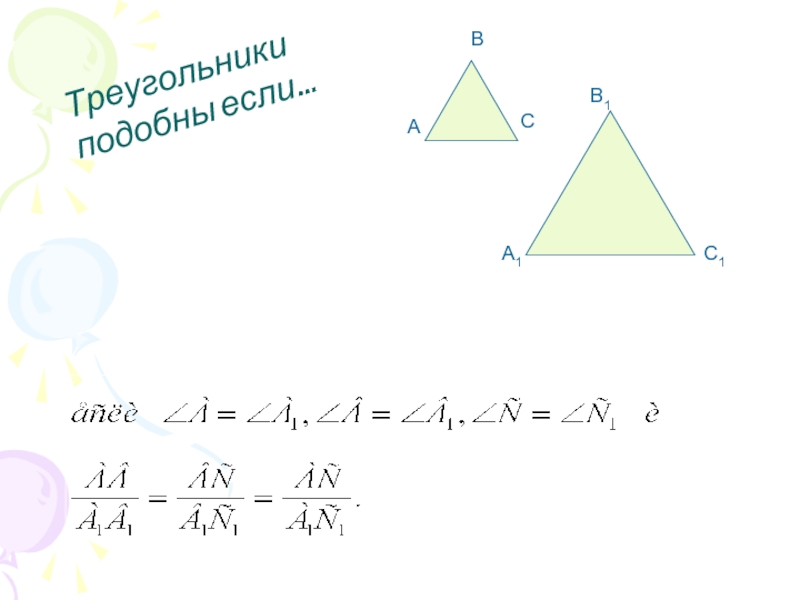
- 3. Это фигуры, которые имеют одинаковую форму.Подобные фигуры
- 4. АВСА1В1С1Треугольники подобны если…
- 5. Устная работа.1). Что такое сходственные стороны треугольников2).
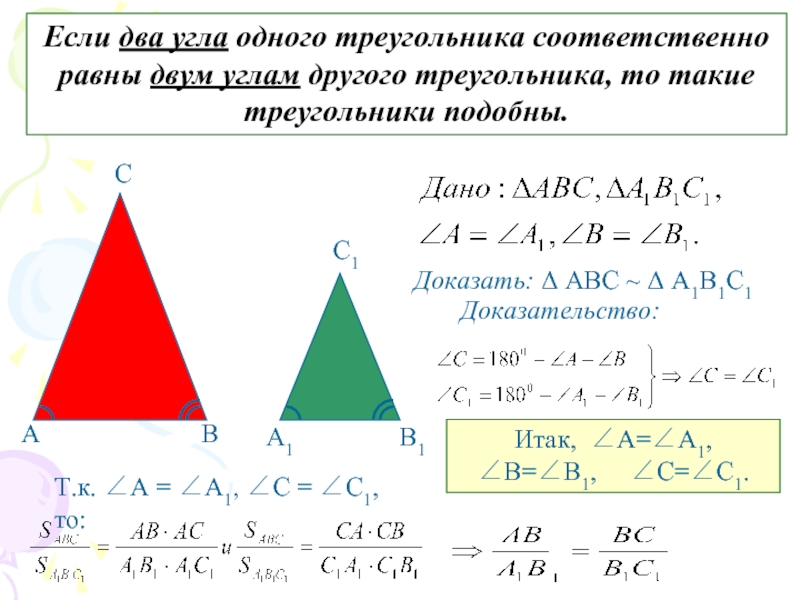
- 6. Если два угла одного треугольника соответственно равны
- 7. 2. Формулировка и доказательство теоремы
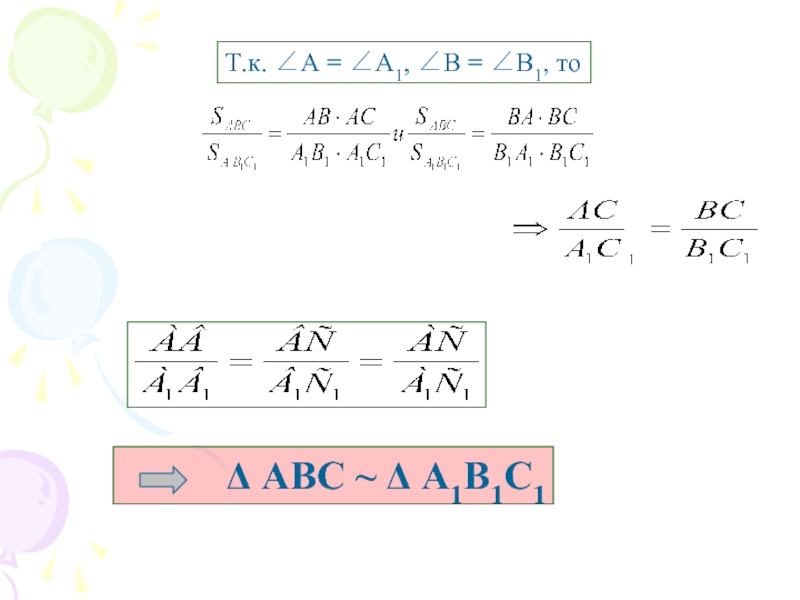
- 8. Т.к. ∠А = ∠А1, ∠В = ∠В1, тоΔ АВС ~ Δ А1В1С1
- 9. 3. Решение задач на применение признака подобия треугольников
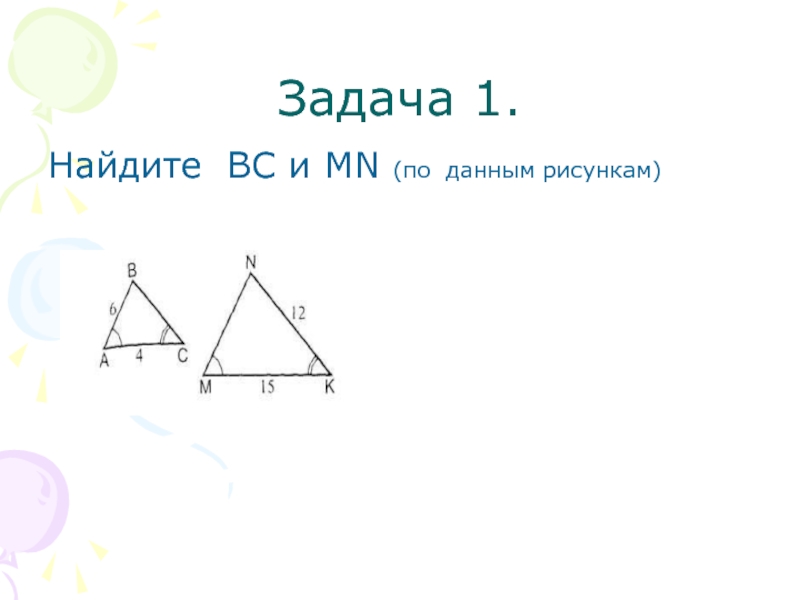
- 10. Задача 1.Найдите ВС и МN (по данным рисункам)
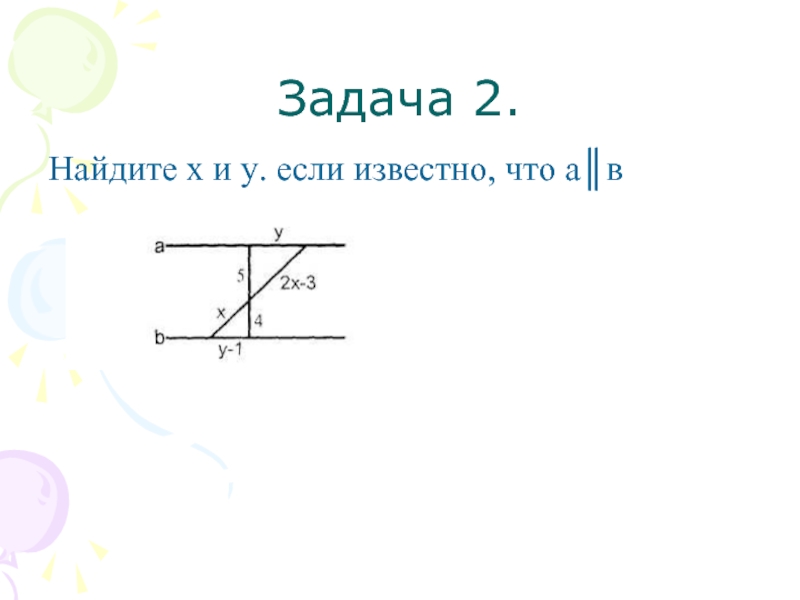
- 11. Задача 2.Найдите х и у. если известно, что а║в
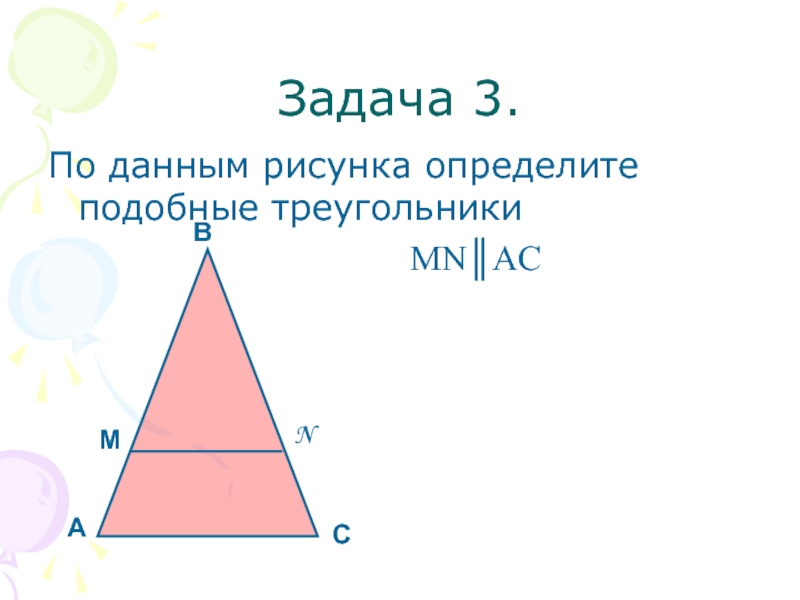
- 12. Задача 3.По данным рисунка определите подобные треугольники
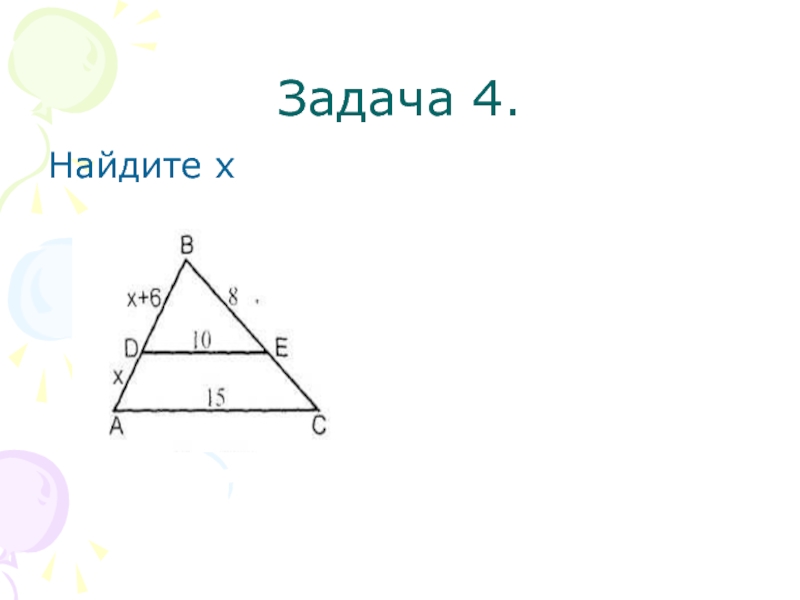
- 13. Задача 4.Найдите х
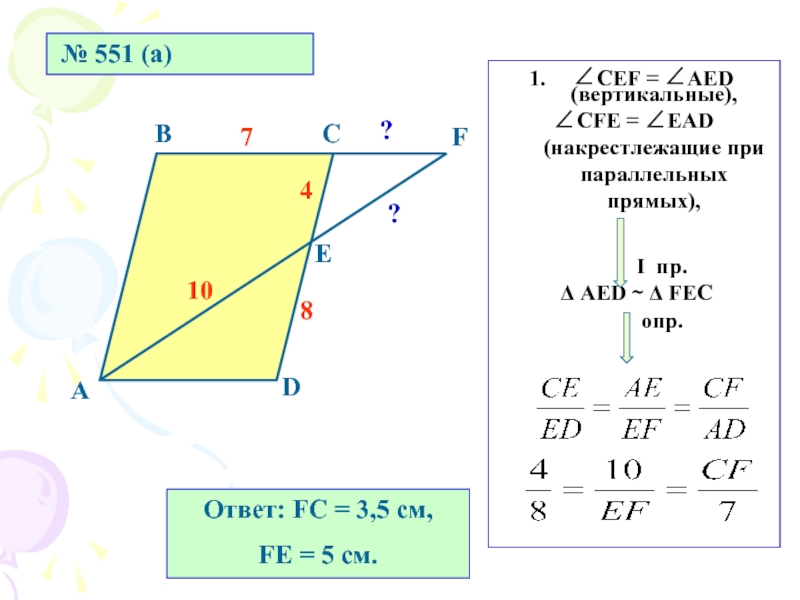
- 14. № 551 (а)АВСDЕF84710??∠СЕF = ∠AED (вертикальные),∠СFE
- 15. Домашняя работап. 59,теорему, № 550, 551 (б)
- 16. Скачать презентанцию
Цель:Повторить определение подобных треугольников, теорему об отношении площадей подобных треугольников Рассмотреть первый признак подобия треугольников, применение его при решении задач
Слайды и текст этой презентации
Слайд 1
8 класс.
Бузецкая Татьяна Валерьевна
Государственное бюджетное общеобразовательное учреждение средняя школа 523
Санкт-Петербурга
Слайд 2Цель:
Повторить определение подобных треугольников, теорему об отношении площадей подобных треугольников
Рассмотреть первый признак подобия треугольников, применение его при решении задач
Слайд 5Устная работа.
1). Что такое сходственные стороны треугольников
2). Что такое коэффициент
подобия?
3). Сформулировать теорему об отношении площадей подобных треугольников.
Слайд 6Если два угла одного треугольника соответственно равны двум углам другого
треугольника, то такие треугольники подобны.
А
В
С
А1
В1
С1
Доказать: Δ АВС ~ Δ А1В1С1
Доказательство:
Т.к.
∠А = ∠А1, ∠С = ∠С1, то:Итак, ∠А=∠А1, ∠В=∠В1, ∠С=∠С1.
Слайд 14 № 551 (а)
А
В
С
D
Е
F
8
4
7
10
?
?
∠СЕF = ∠AED (вертикальные),
∠СFE = ∠EAD (накрестлежащие
при параллельных прямых),
I
пр.Δ АЕD ∼ Δ FЕС
опр.
Ответ: FC = 3,5 см,
FЕ = 5 см.
Теги