Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Правильные многогранники в мире
Содержание
- 1. Правильные многогранники в мире
- 2. Актуализация знаний Какой раздел симметрии мы с
- 3. 4. Как можно назвать все эти фигуры?5. Что характерно для каждого из них?
- 4. 6. Перед вами несколько многогранников. Какой из них лишний?
- 5. Выпуклый многогранник называется правильным, если все его
- 6. Свойства правильных многогранников:он выпуклыйвсе его грани являются
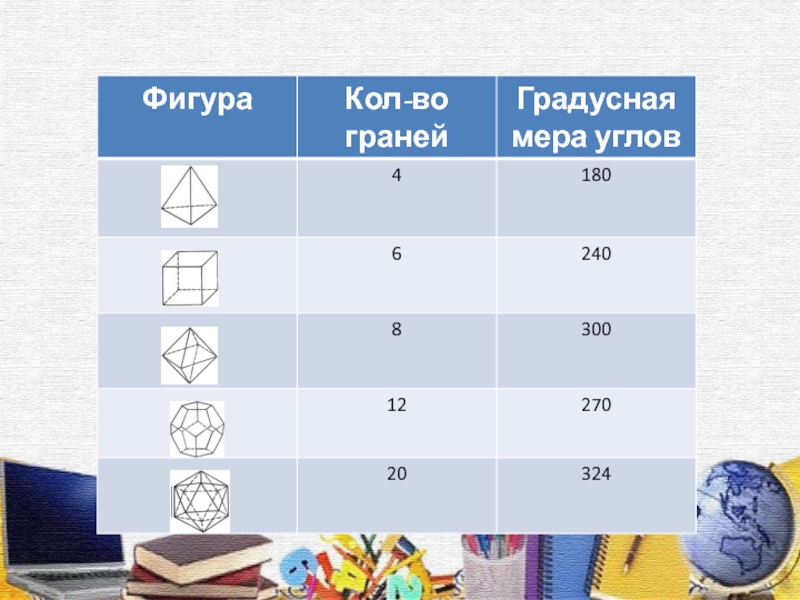
- 7. Сколько существует правильных многогранников ?
- 8. Слайд 8
- 9. Слайд 9
- 10. Пять правильных многогранниковТЕТРАЭДР – правильный многогранник, поверхность
- 11. Многогранники или Платоновы телаВ школах Пифагора
- 12. Тетраэдр-огонь
- 13. Куб-земля
- 14. Октаэдр-воздух
- 15. Икосаэдр-вода
- 16. Додекаэдр-вселенная
- 17. Вселенная говорит с нами на языке геометрии.
- 18. Кубок КеплераВсе та же вера в гармонию,
- 19. Изучая любые многогранники, естественнее всего подсчитать, сколько
- 20. Слайд 20
- 21. Теорема ЭйлераДля любого выпуклого многогранника справедливо соотношение:
- 22. Многогранники в нашей жизни
- 23. Многогранники в архитектуреВеликая пирамида в Гизе-
- 24. ЛуврЛувр-один из крупнейших и самый популярный художественный музей
- 25. Национальная библиотека БеларусиВизитная карточка Республики Беларусь -
- 26. Башня Сююмбике Башня Сююмбике состоит из семи
- 27. Многогранники в искусствеЛеонардо да Винчи - «Портрет
- 28. Многогранники в химииНекоторые атомные ядра могут иметь
- 29. Многогранники в биологии« Природа вскармливает на своем
- 30. Задача: Определите количество граней, вершин и рёбер
- 31. 1.Ввести понятие правильного многогранника.2. Рассмотреть все виды
- 32. Тестирование: 1. Поверхность, составленная из четырех треугольников
- 33. 5. Высота боковой грани правильной пирамиды, проведенная
- 34. Проверь себя!1. A2. B3. C4. A5. B6. D7. C8. D
- 35. СПАСИБО ЗА ВНИМАНИЕ!ВСЕ УМНИЧКИ!
- 36. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Мир правильных многогранников
Выполнила:
Преподаватель математики
Кузнецова Анна Игоревна
Государственное бюджетное профессиональное бюджетное
учреждение «Себряковский Технологический Техникум»
Слайд 2Актуализация знаний
Какой раздел симметрии мы с вами сейчас проходим?
Какие
бывают многогранники?
Какие многогранники вы уже знаете?
Слайд 5Выпуклый многогранник называется правильным, если все его грани – равные
правильные многоугольники и в каждой вершине сходится одно и то
же число граней.Выпуклый многогранник называется правильным, если все его грани – равные правильные многоугольники и все двугранные углы при всех ребрах равны между собой.
Определение правильного многогранника
Слайд 6Свойства правильных многогранников:
он выпуклый
все его грани являются равными правильными многоугольниками
в
каждой его вершине сходится одинаковое число граней
все его двугранные углы
равныСлайд 10Пять правильных многогранников
ТЕТРАЭДР – правильный многогранник, поверхность которого состоит из
четырех правильных треугольников
ГЕКСАЭДР (КУБ) – правильный многогранник, поверхность которого состоит
из шести правильных четырехугольников (квадратов). ОКТАЭДР – правильный многогранник, поверхность которого состоит из восьми правильных треугольников
ИКОСАЭДР – правильный многогранник, поверхность которого состоит из двадцати правильных треугольников.
ДОДЕКАЭДР – правильный многогранник, поверхность которого состоит из двенадцати правильных пятиугольников.
Названия этих многогранников пришли из Древней Греции, и в них указывается число граней:
«эдра» - грань
«тетра» - 4
«гекса» - 6
«окта» - 8
«икоса» - 20
«додека» - 12
Слайд 11Многогранники или
Платоновы тела
В школах Пифагора и Платона пять геометрических
тел считались отображением божественных измерений энергий. Каждому геометрическому телу соответствовала
определённая стихия: куб – Земля, икосаэдр – Вода, тетраэдр – Огонь, октаэдр – Воздух, додекаэдр – Вселенная. Сечение этих геометрических тел даёт плоские геометрические фигуры: Земля – квадрат, Вода – шестиугольник, Огонь – треугольник, Воздух – ромб, Эфир – восьмиугольник.Слайд 17Вселенная говорит с нами на языке геометрии. Перечисленные выше геометрические
тела – многогранники и их сечения – плоские фигуры –
по своей сути являются преобразователями энергий в соответствии с природными явлениями. Таким образом, эти многогранники, отражающие энергии стихий, для человека являются связующим звеном с Природой.Слайд 18Кубок Кеплера
Все та же вера в гармонию, красоту и математически
закономерное устройство мироздания привела И. Кеплера к мысли о том,
что поскольку существует пять правильных многогранников, то им соответствуют только шесть планет. По его мнению, сферы планет связаны между собой вписанными в них Платоновыми телами. Поскольку для каждого правильного многогранника центры вписанной и описанной сфер совпадают, то вся модель будет иметь единый центр, в котором будет находиться Солнце.Геометрическая модель Солнечной системы,
основанная на «платоновых телах».
В сферу орбиты Сатурна он вписывает куб, в куб - сферу Юпитера, в сферу Юпитера - тетраэдр, и так далее последовательно вписываются друг в друга сфера Марса - додекаэдр, сфера Земли - икосаэдр, сфера Венеры - октаэдр, сфера Меркурия
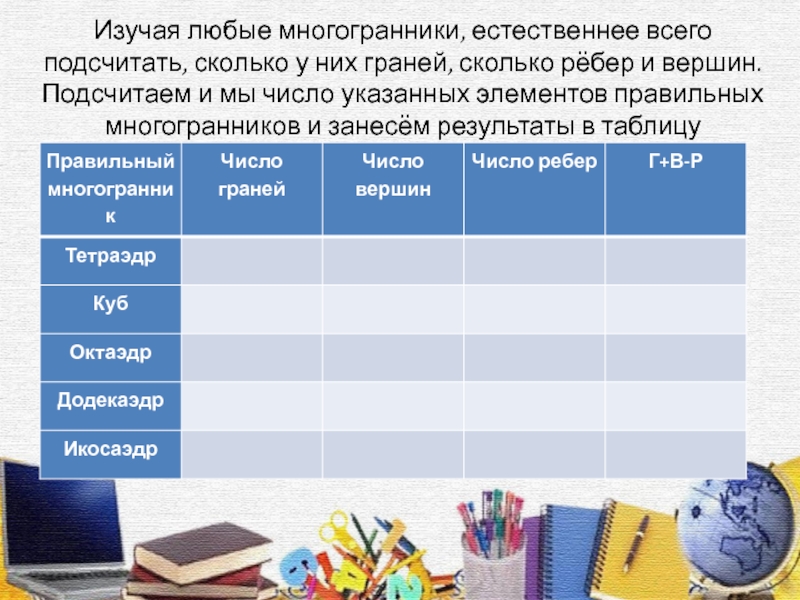
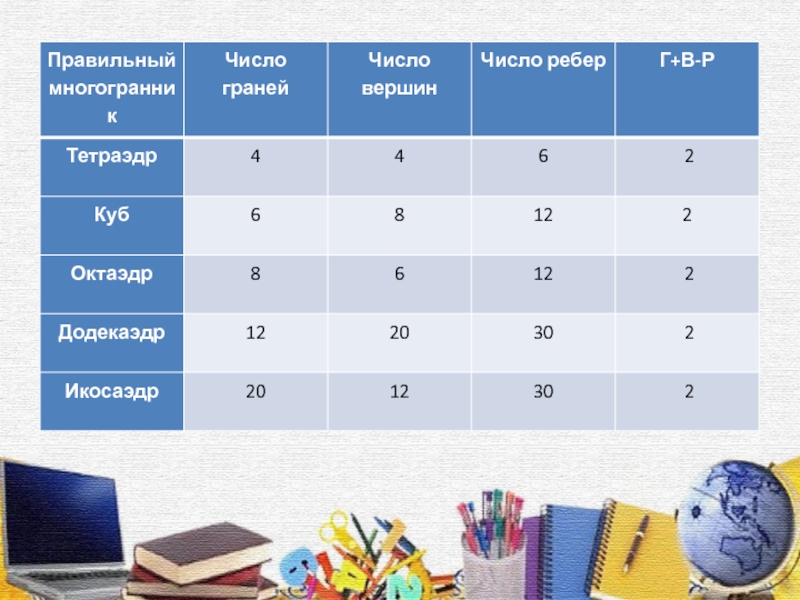
Слайд 19Изучая любые многогранники, естественнее всего подсчитать, сколько у них граней,
сколько рёбер и вершин. Подсчитаем и мы число указанных элементов
правильных многогранников и занесём результаты в таблицуСлайд 21Теорема Эйлера
Для любого выпуклого многогранника справедливо соотношение: Г+В-Р=2, где Г-число
граней, В-число вершин, Р- число ребер данного многогранника.
Грани +
Вершины - Рёбра = 2.Слайд 23Многогранники в
архитектуре
Великая пирамида в Гизе- это грандиозная Египетская пирамида
является древнейшим из семи чудес Древности. Кроме того, это единственное
из чудес света, сохранившееся до наших дней. Во время своего создания Великая пирамида была самым высоким сооружением в мире.Слайд 24Лувр
Лувр-один из крупнейших и самый популярный художественный музей мира. Музей расположен
в центре Парижа, на правом берегу Сены, на улице Риволи, в 1-м округе столицы
Слайд 25Национальная библиотека Беларуси
Визитная карточка Республики Беларусь - новое здание Национальной
библиотеки в Минске. Проект нового здания был разработан еще в
конце 80-х годов прошлого века и в 1989 году стал победителем на всесоюзном конкурсе. Однако воплотить его в жизнь удалось лишь спустя более чем 15 лет.Слайд 26Башня Сююмбике
Башня Сююмбике состоит из семи ярусов, нижние ярусы
представляют из себя параллелепипеды а верхние - многогранники.
Спасская башня Кремля
Четыре
яруса башни представляют из себя куб, многогранники и пирамиду.Слайд 27Многогранники в искусстве
Леонардо да Винчи - «Портрет Монны Лизы».
Композиция
рисунка основана на золотых треугольниках, являющихся частями правильного звездчатого пятиугольника.
Альбрехт
Дюрер - гравюра «Меланхолия». На переднем плане картины изображен додекаэдр.
Сальвадор Дали – «Тайная Вечеря».
Христос со своими учениками изображён на фоне огромного прозрачного додекаэдр.
Слайд 28Многогранники в химии
Некоторые атомные ядра могут иметь вид правильных многогранников
с округлѐнными углами.
Кристаллы являются природными многогранниками
(соль,лёд и т.д)
Слайд 29Многогранники в биологии
« Природа вскармливает на своем лоне неисчерпаемое количество
удивительных созданий, которые по красоте и разнообразию далеко превосходят все
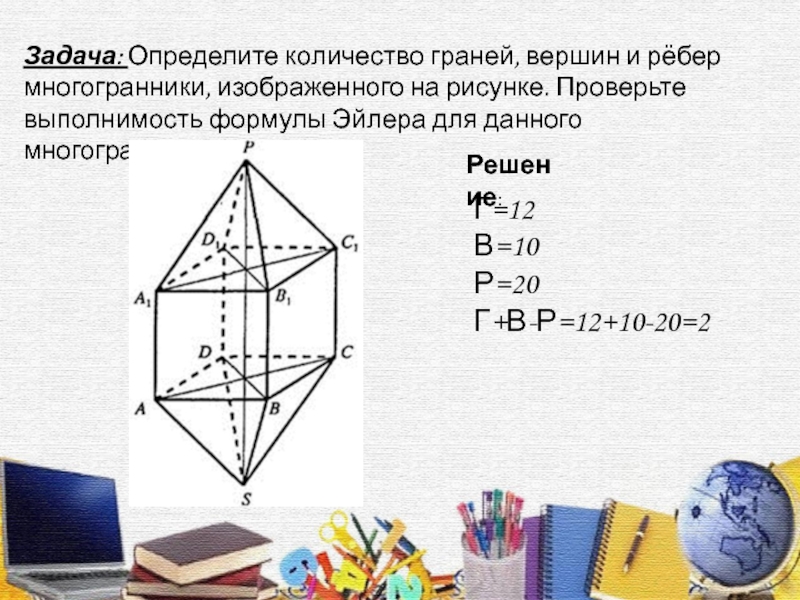
созданные искусством человека формы». Действительно, построенные пчелами соты строго параллельны, расстояния между ними выдерживаются с удивительным постоянством. Пчелиные ячейки представляют собой шестигранные геометрические фигуры.Слайд 30Задача: Определите количество граней, вершин и рёбер многогранники, изображенного на
рисунке. Проверьте выполнимость формулы Эйлера для данного многогранника.
Решение:
Г=12
В=10
Р=20
Г+В-Р=12+10-20=2
Слайд 311.Ввести понятие правильного многогранника.
2. Рассмотреть все виды правильных многогранников.
3. Показать
влияние правильных многогранников на возникновение философских теорий и фантастических гипотез..
4.
Показать связь многогранников в нашей жизни.Задачи урока:
Слайд 32Тестирование:
1. Поверхность, составленная из четырех треугольников
А) ТЕТРАЭДР
B) ПАРАЛЛЕЛЕПИПЕД С) КВАДРАТ D) ШАР
2. Поверхность,
составленная из многоугольников и ограничива- ющая некоторое геометрическое телоА) МНОГОУГОЛЬНИК B) МНОГОГРАННИК С) ТРЕУГОЛЬНИК D) КВАДРАТ
3. Многоугольник, из которого составлен многогранник
А) СТОРОНА B) РЕБРО С) ГРАНЬ D) ВЕРШИНА
4. Отрезок, соединяющий две вершины, не принадлежащие одной грани
А) ДИАГОНАЛЬ B) МЕДИАНА С) ВЫСОТА D) АПОФЕМА
Слайд 335. Высота боковой грани правильной пирамиды, проведенная из ее вершины
А) ДИАГОНАЛЬ B) АПОФЕМА С) КАТЕТ
D)ГИПОТЕЗА6. Этот правильный многогранник составлен из 8-ми равносторонних треугольников
А) КВАДРАТ B) ТЕТРАЭДР С) ДОДЕКАЭДР D) ОКТАЭДР
7. Составлен из 6-ти правильных четырехугольников
А) КВАДРАТ B) ТЕТРАЭДР С) КУБ D) ПИРАМИДА
8. Стихия тетраэдра
А) ВОДА B) ВОЗДУХ С) ЗЕМЛЯ D) ОГОНЬ