Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Преобразование графиков функции
Содержание
- 1. Преобразование графиков функции
- 2. Цели:1) Систематизировать приемы построения графиков.2) Показать их применение при
- 3. Рассмотрим основные правила преобразования графиков на примерах элементарных функций
- 4. 1) Преобразование симметрии относительно оси x f(x)→-f(x)График
- 5. 2) Преобразование симметрии относительно оси y f(x)→f(-x)График
- 6. 3) Параллельный перенос вдоль оси x
- 7. 4) Параллельный перенос вдоль оси y
- 8. 5) Сжатие и растяжение вдоль оси x
- 9. 6) Сжатие и растяжение вдоль оси y
- 10. 7) Построение графика функции y=|f(x)|Части графика функции
- 11. 8) Построение графика функции y=f(|x|)Часть графика функции
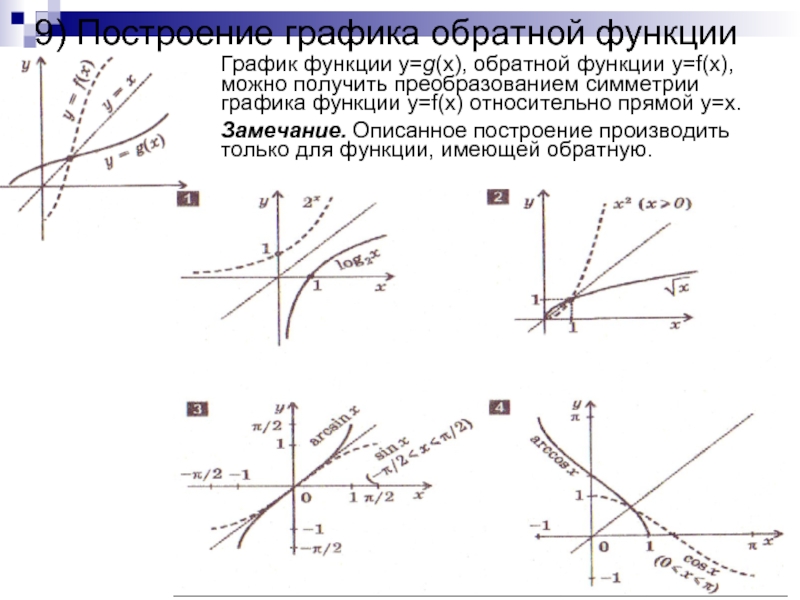
- 12. 9) Построение графика обратной функцииГрафик функции y=g(x),
- 13. Построение графиков сложных функций с помощью последовательных преобразований графиков элементарных функций (на примерах)
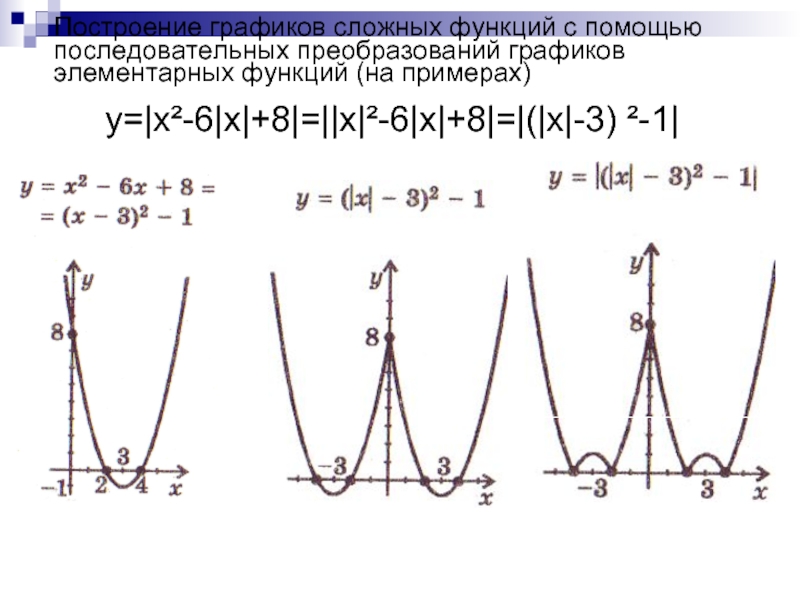
- 14. Построение графиков сложных функций с помощью последовательных преобразований графиков элементарных функций (на примерах)y=|x²-6|x|+8|=||x|²-6|x|+8|=|(|x|-3) ²-1|
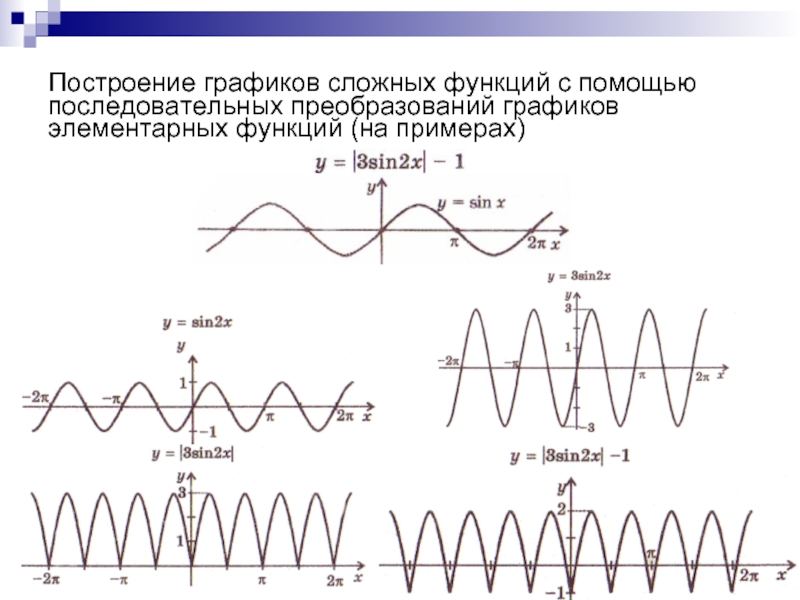
- 15. Построение графиков сложных функций с помощью последовательных преобразований графиков элементарных функций (на примерах)
- 16. Построение графиков сложных функций с помощью последовательных преобразований графиков элементарных функций (на примерах)
- 17. Применение правил преобразования графиков при решении заданий ЕГЭ (части C).
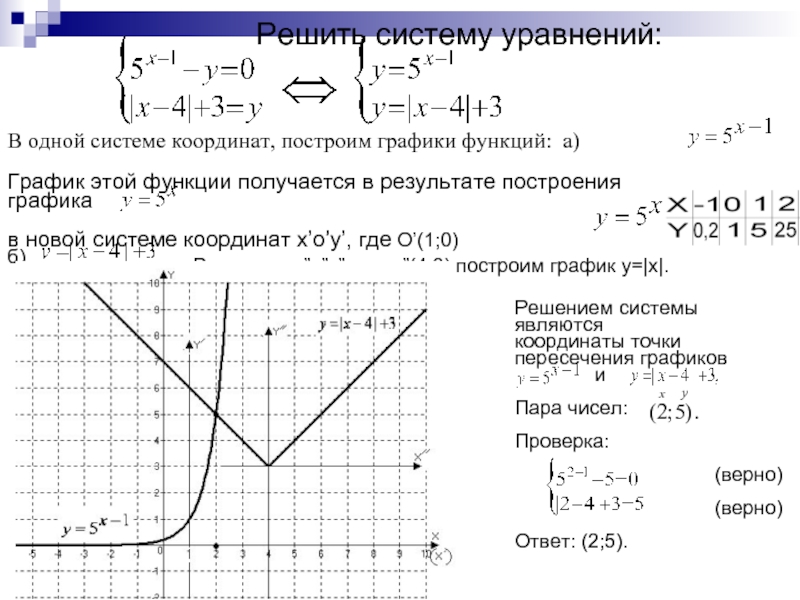
- 18. Решить систему уравнений:В одной системе координат, построим
- 19. Решить уравнение: f(g(x))+g(f(x))=32, если известно, что иРешение: Преобразуем
- 20. а) График данной функции получается построением графикаВ
- 21. Вывод:Мы видим, что правила преобразования графиков существенно
- 22. Тема: «Преобразование графиков функции»
- 23. Скачать презентанцию
Цели:1) Систематизировать приемы построения графиков.2) Показать их применение при построении: а) графиков сложных функций; б) при решении заданий ЕГЭ из части C.
Слайды и текст этой презентации
Слайд 2Цели:
1) Систематизировать приемы построения графиков.
2) Показать их применение при построении:
а) графиков сложных
функций;
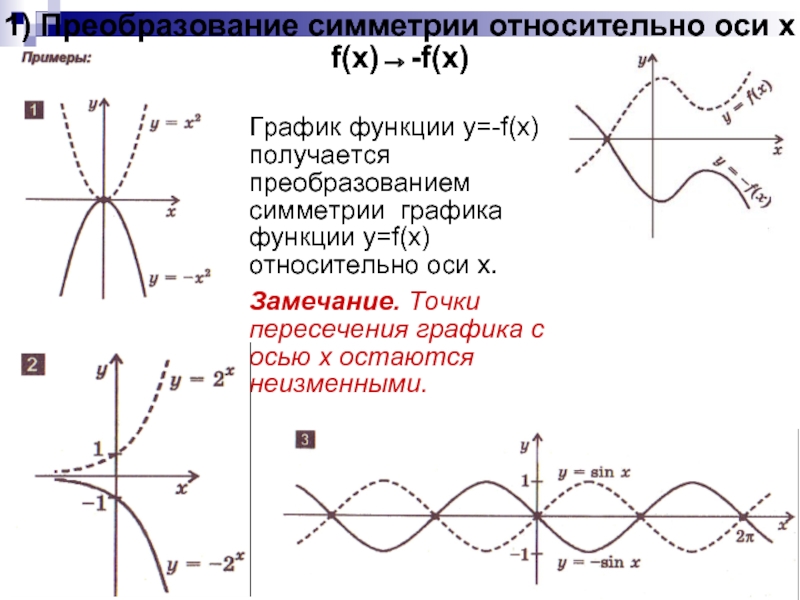
Слайд 41) Преобразование симметрии относительно оси x
f(x)→-f(x)
График функции y=-f(x) получается преобразованием
симметрии графика функции y=f(x) относительно оси x.
Замечание. Точки пересечения графика
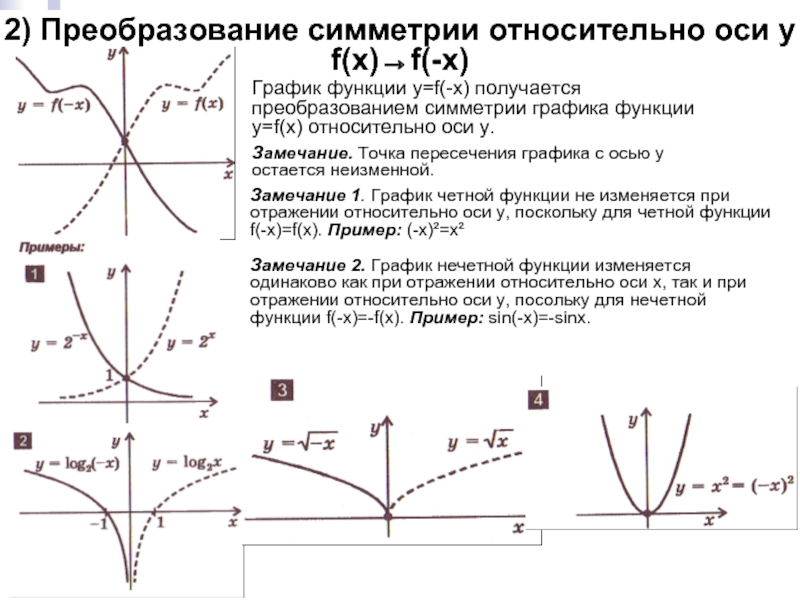
с осью x остаются неизменными.
Слайд 52) Преобразование симметрии относительно оси y
f(x)→f(-x)
График функции y=f(-x) получается преобразованием
симметрии графика функции y=f(x) относительно оси y.
Замечание. Точка пересечения графика
с осью y остается неизменной.Замечание 1. График четной функции не изменяется при отражении относительно оси y, поскольку для четной функции f(-x)=f(x). Пример: (-x)²=x²
Замечание 2. График нечетной функции изменяется одинаково как при отражении относительно оси x, так и при отражении относительно оси y, посольку для нечетной функции f(-x)=-f(x). Пример: sin(-x)=-sinx.
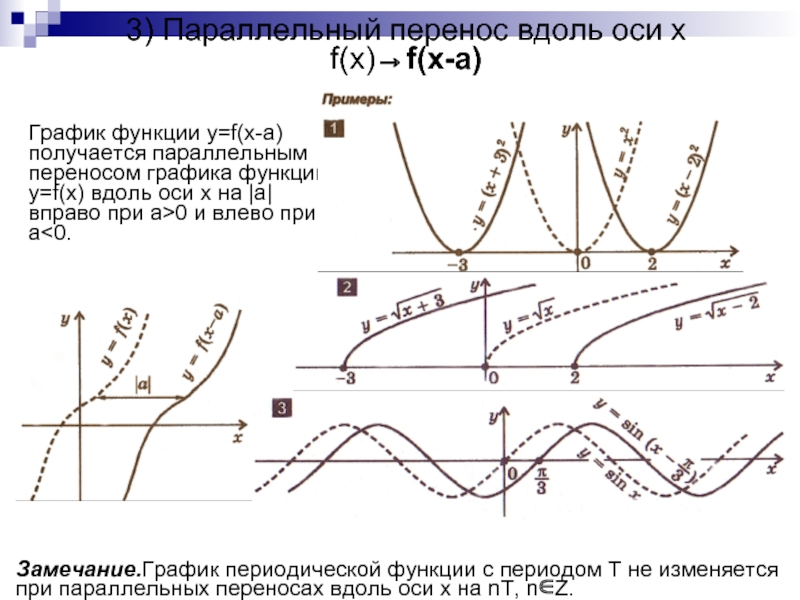
Слайд 63) Параллельный перенос вдоль оси x
f(x)→f(x-a)
График функции y=f(x-a) получается
параллельным переносом графика функции y=f(x) вдоль оси x на |a|
вправо при a>0 и влево при a<0.Замечание.График периодической функции с периодом T не изменяется при параллельных переносах вдоль оси x на nT, n∈Z.
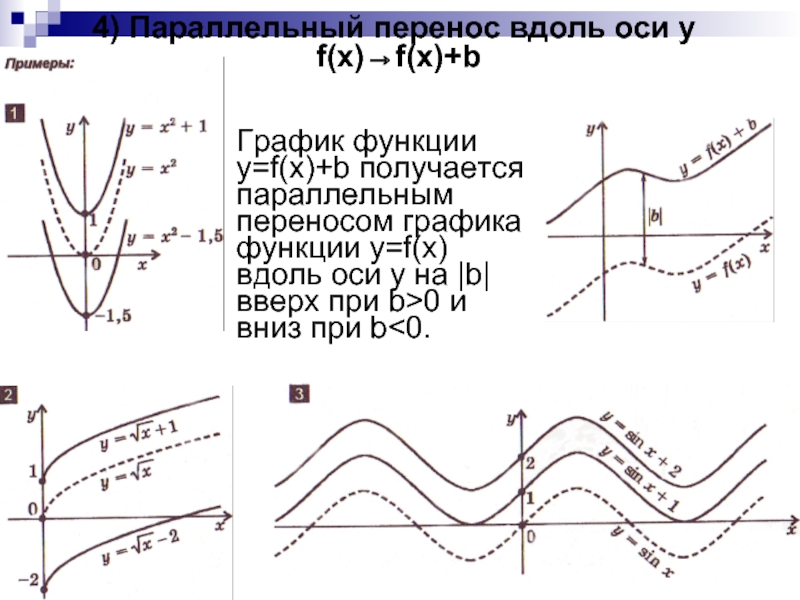
Слайд 74) Параллельный перенос вдоль оси y
f(x)→f(x)+b
График функции y=f(x)+b
получается параллельным переносом графика функции y=f(x) вдоль оси y на
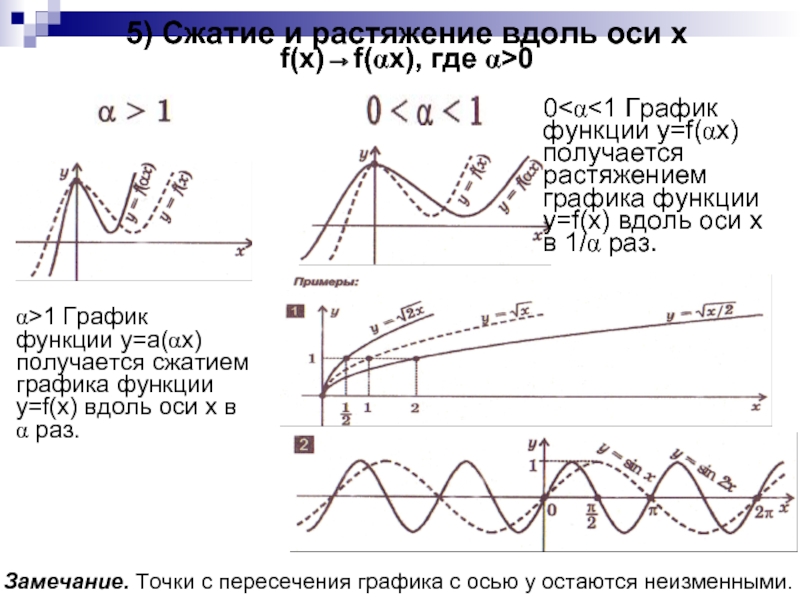
|b| вверх при b>0 и вниз при b<0.
Слайд 85) Сжатие и растяжение вдоль оси x
f(x)→f(αx), где α>0
α>1 График
функции y=а(αx) получается сжатием графика функции y=f(x) вдоль оси x
в α раз.Замечание. Точки с пересечения графика с осью y остаются неизменными.
0<α<1 График функции y=f(αx) получается растяжением графика функции y=f(x) вдоль оси x в 1/α раз.
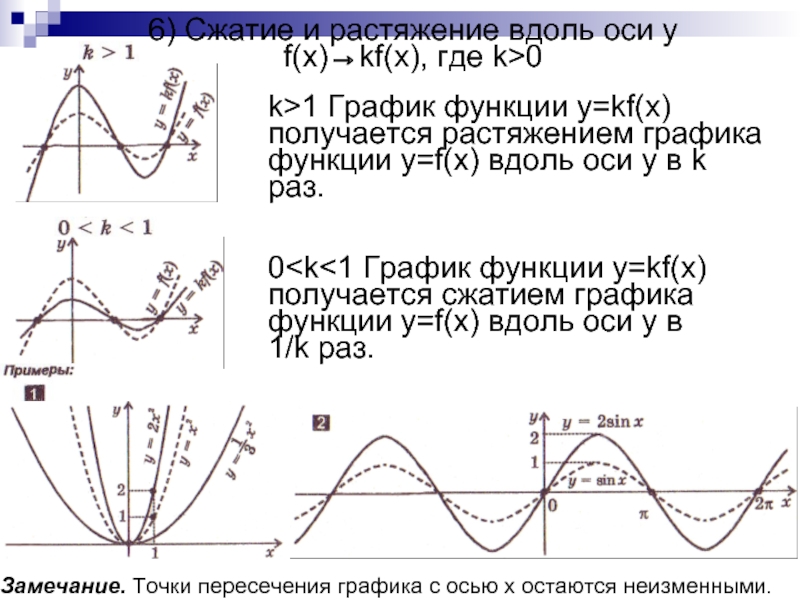
Слайд 96) Сжатие и растяжение вдоль оси y
f(x)→kf(x), где k>0
k>1 График
функции y=kf(x) получается растяжением графика функции y=f(x) вдоль оси y
в k раз.0 Замечание. Точки пересечения графика с осью x остаются неизменными.
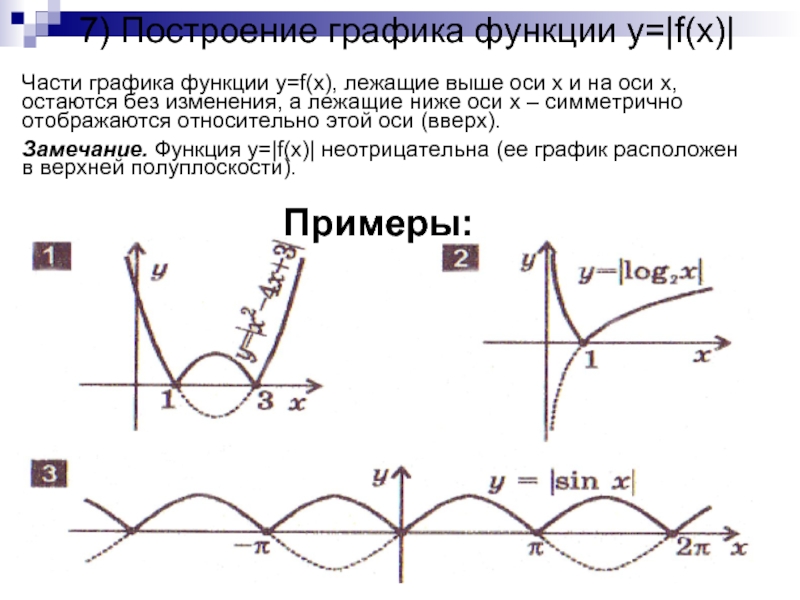
Слайд 107) Построение графика функции y=|f(x)|
Части графика функции y=f(x), лежащие выше
оси x и на оси x, остаются без изменения, а
лежащие ниже оси x – симметрично отображаются относительно этой оси (вверх).Замечание. Функция y=|f(x)| неотрицательна (ее график расположен в верхней полуплоскости).
Примеры:
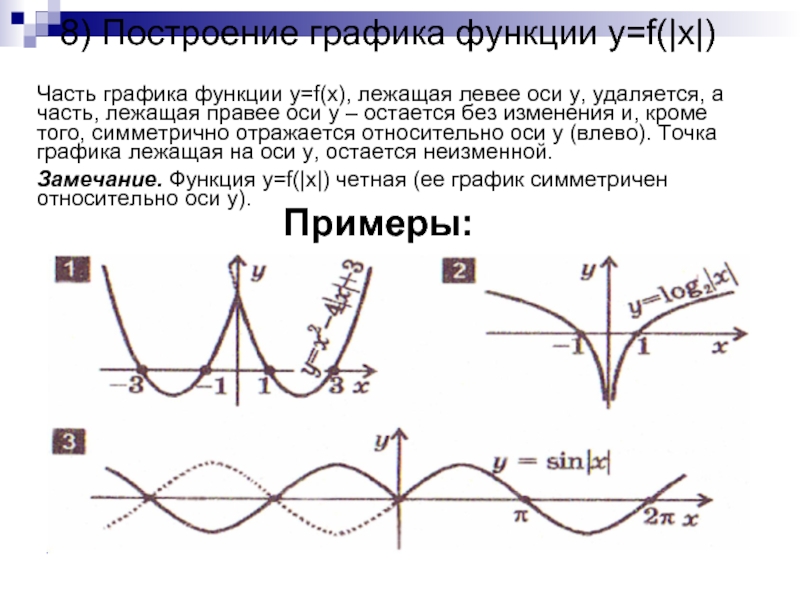
Слайд 118) Построение графика функции y=f(|x|)
Часть графика функции y=f(x), лежащая левее
оси y, удаляется, а часть, лежащая правее оси y –
остается без изменения и, кроме того, симметрично отражается относительно оси y (влево). Точка графика лежащая на оси y, остается неизменной.Замечание. Функция y=f(|x|) четная (ее график симметричен относительно оси y).
Примеры:
Слайд 129) Построение графика обратной функции
График функции y=g(x), обратной функции y=f(x),
можно получить преобразованием симметрии графика функции y=f(x) относительно прямой y=x.
Замечание.
Описанное построение производить только для функции, имеющей обратную. 
Слайд 13Построение графиков сложных функций с помощью последовательных преобразований графиков элементарных
функций (на примерах)
Слайд 14Построение графиков сложных функций с помощью последовательных преобразований графиков элементарных
функций (на примерах)
y=|x²-6|x|+8|=||x|²-6|x|+8|=|(|x|-3) ²-1|
Слайд 15Построение графиков сложных функций с помощью последовательных преобразований графиков элементарных
функций (на примерах)
Слайд 16Построение графиков сложных функций с помощью последовательных преобразований графиков элементарных
функций (на примерах)
Слайд 18Решить систему уравнений:
В одной системе координат, построим графики функций: а)
График этой функции получается в результате построения графика
в новой
системе координат x’o’y’, где O’(1;0) б)
В системе x”o”y”, где o”(4;3) построим график y=|x|.
Слайд 19Решить уравнение: f(g(x))+g(f(x))=32, если известно, что и
Решение: Преобразуем функцию f(x).
Так как
, то
Тогда g(f(x))=20.
Подставим в уравнение f(g(x))+g(f(x))=32, получим f(g(x))+20=32;
f(g(x))=12
Пусть g(x)=t,
тогда f(t)=12 или при
при
или
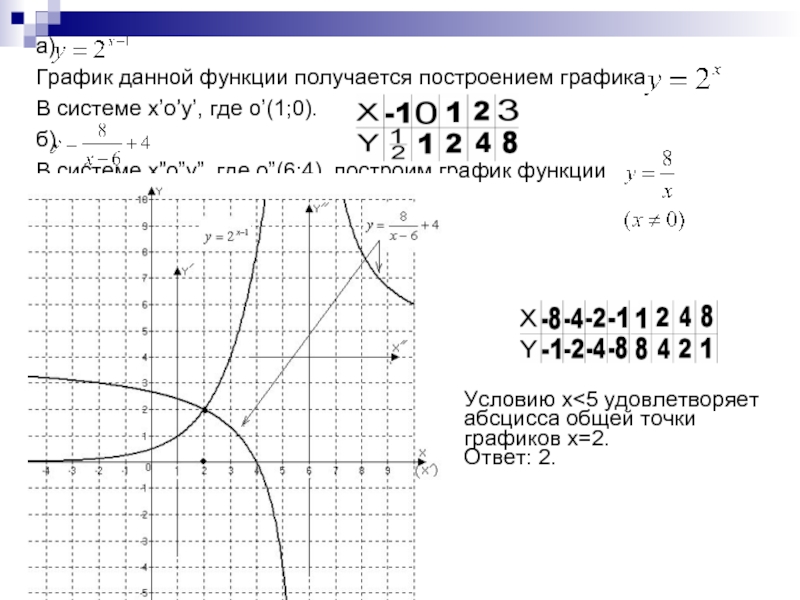
Слайд 20а)
График данной функции получается построением графика
В системе x’o’y’, где
o’(1;0).
б)
В системе x”o”y”, где o”(6;4), построим график функции
Условию
x<5 удовлетворяет абсцисса общей точки графиков x=2. Ответ: 2.
Слайд 21Вывод:
Мы видим, что правила преобразования графиков существенно упрощают построение графиков
сложных функций.
Помогают найти нетрадиционное решение сложных задач.
Теги
