Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация для урока по теме: "Теорема Пифогора"
Содержание
- 1. Презентация для урока по теме: "Теорема Пифогора"
- 2. «Да, путь познания не гладок.Но знаем мы со школьных лет,Загадок больше, чем разгадок,И поискам предела нет!»
- 3. Сторона квадрата равна 9 см. Найдите его
- 4. Теорема Пифагора
- 5. о. Самос
- 6. Найди длину лестницы, приставленной к дому, если
- 7. «Геометрия владеет двумя сокровищами: одно из них – это теорема Пифагора»
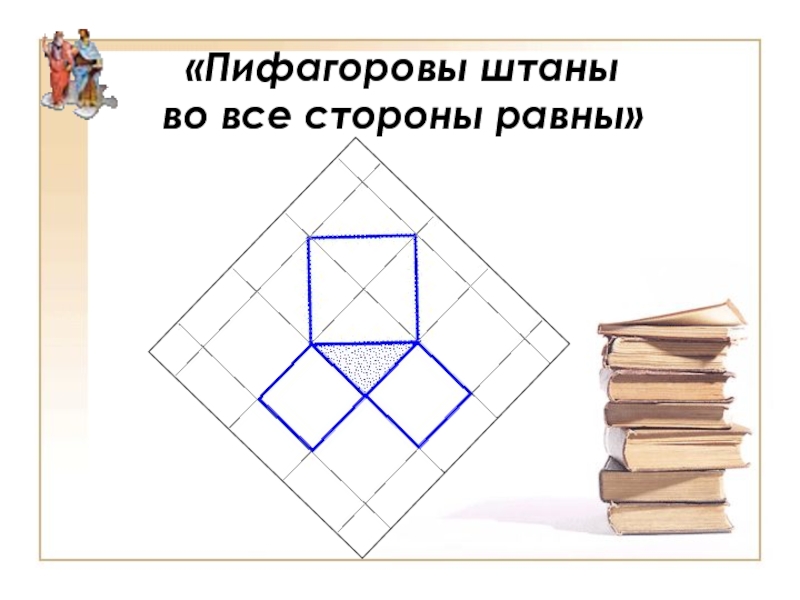
- 8. «Пифагоровы штаны во все стороны равны»
- 9. «Квадрат, построенный на гипотенузе прямо-угольного треугольника, равновелик
- 10. Если дан нам треугольникИ притом с прямым
- 11. Теорема ПифагораВ прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов
- 12. Дано: прямоугольный треугольник ,а и b –
- 13. с² = а2 + b2№ 483 -
- 14. Дано: ΔKDL, ∠ D = 90°, DL=6м, KD=8мНайти: KLРешение: По теореме Пифагора KL²=DL²+DK², KL²=36+64=100, KL²=100, KL=10мОтвет: KL=10м
- 15. Три стороны четырехугольника имеют длины 4см, 7см
- 16. № 493Найдите сторону и площадь ромба, если
- 17. О теореме Пифагора Пребудет вечной
- 18. «Сегодня на уроке я повторил…»«Сегодня на уроке я узнал…»«Сегодня на уроке я научился…»ИТОГ УРОКА
- 19. Домашнее заданиеп. 54 задачи: № 483 (б,
- 20. Урок закончен!
- 21. Скачать презентанцию
«Да, путь познания не гладок.Но знаем мы со школьных лет,Загадок больше, чем разгадок,И поискам предела нет!»
Слайды и текст этой презентации
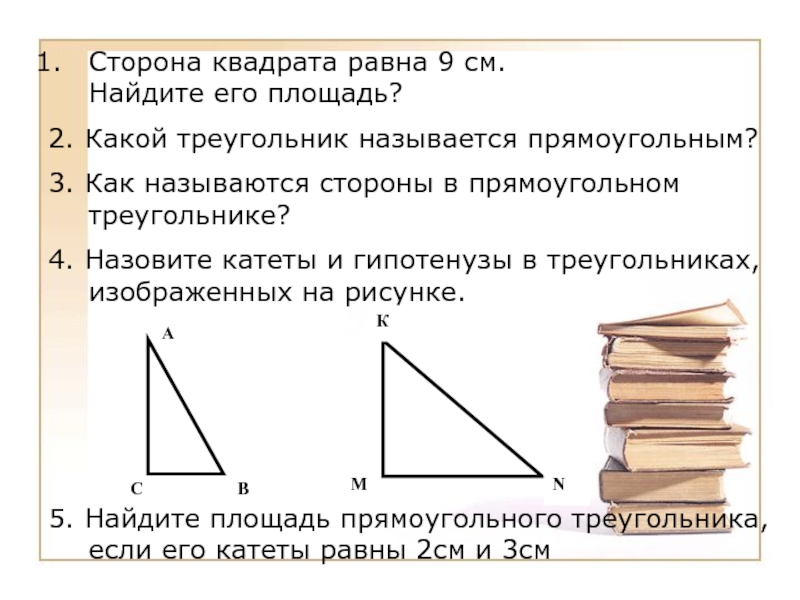
Слайд 3Сторона квадрата равна 9 см.
Найдите его площадь?
2. Какой
треугольник называется прямоугольным?
3. Как называются стороны в прямоугольном треугольнике?
4. Назовите
катеты и гипотенузы в треугольниках, изображенных на рисунке.5. Найдите площадь прямоугольного треугольника, если его катеты равны 2см и 3см
Слайд 6 Найди длину лестницы, приставленной к дому, если один ее конец
находится на расстоянии 6м от другого, а другой на стыке
стены и крыши. Высота дома равна 8м.DL=6м, KD=8м
KL-?
Слайд 9
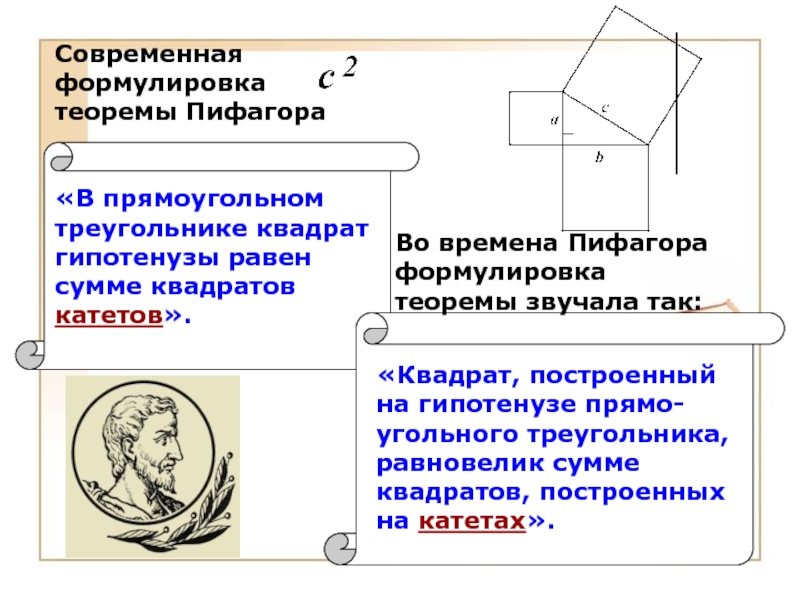
«Квадрат, построенный на гипотенузе прямо-угольного треугольника, равновелик сумме квадратов, построенных
на катетах».
«В прямоугольном
треугольнике квадрат
гипотенузы равен
сумме квадратов катетов».
Во времена
Пифагора формулировка теоремы звучала так:Современная формулировка
теоремы Пифагора
Слайд 10Если дан нам треугольник
И притом с прямым углом,
То квадрат гипотенузы
Мы
всегда легко найдем:
Катеты в квадрат возводим,
Сумму степеней находим —
И таким
простым путемК результату мы придем
И. Дырченко
Слайд 11Теорема Пифагора
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов
Слайд 12Дано: прямоугольный треугольник ,
а и b – катеты
с –
гипотенуза
Доказать: с²=а²+b²
Доказательство:
1) Достроим треугольник до квадрата со стороной а+b
2)
Площадь этого квадрата равна S=(a+b)23) С другой стороны этот квадрат состоит
из четырех равных прямоугольных треугольников, площадь каждого из которых равна ½ab, и квадрата со стороной с, поэтому S= 4½ab +с2.
4) Приравняем площадь квадрата
(a+b)2=2 ab +с2
а2+2 ab+b2=2 ab +с2
а2+ b2=с2
Теорема доказана
Слайд 13с² = а2 + b2
№ 483 - 484
5
4
3
8
13
6
c
b
а
12
5
10
В прямоугольном треугольнике
а и b – катеты,
с – гипотенуза. Заполните таблицу.
b2
=c²-a² а2 =c²-b²
Слайд 14Дано: ΔKDL, ∠ D = 90°, DL=6м, KD=8м
Найти: KL
Решение: По
теореме Пифагора
KL²=DL²+DK²,
KL²=36+64=100,
KL²=100,
KL=10м
Ответ: KL=10м
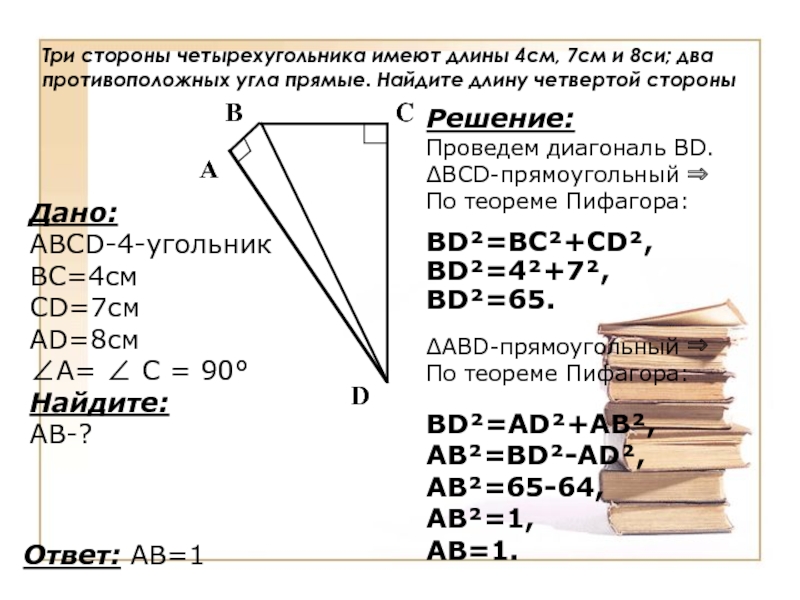
Слайд 15Три стороны четырехугольника имеют длины 4см, 7см и 8си; два
противоположных угла прямые. Найдите длину четвертой стороны
Решение:
Проведем диагональ ВD.
ΔBCD-прямоугольный ⇒
По
теореме Пифагора:BD²=BC²+CD², BD²=4²+7², BD²=65.
ΔABD-прямоугольный ⇒
По теореме Пифагора:
BD²=AD²+AB²,
AB²=BD²-AD²,
AB²=65-64,
AB²=1,
AB=1.
Ответ: AB=1
Слайд 16
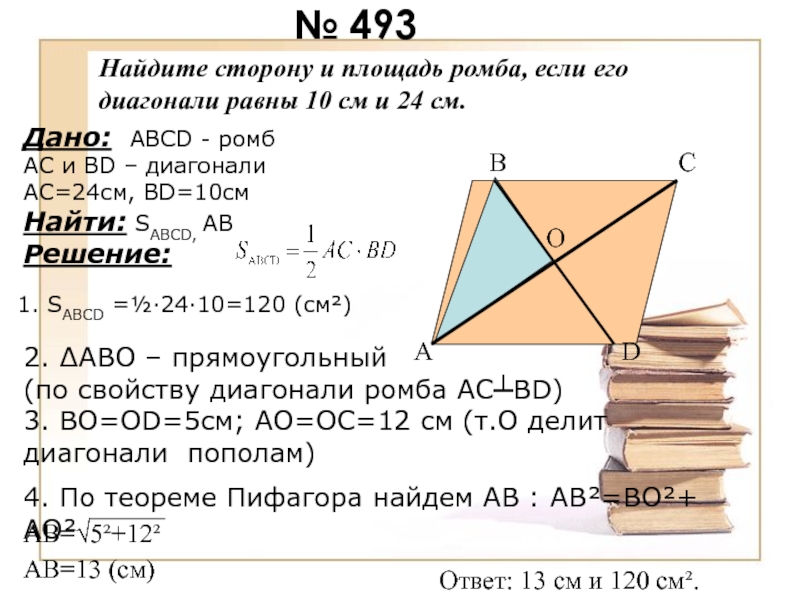
№ 493
Найдите сторону и площадь ромба, если его диагонали равны
10 см и 24 см.
1. SABCD =½·24·10=120 (cм²)
2. ∆ABO –
прямоугольный
(по свойству диагонали ромба АС┴ВD)
3. ВО=ОD=5см; АО=ОС=12 см (т.О делит диагонали пополам)4. По теореме Пифагора найдем АВ : АВ²=ВО²+ АО²
O
АВ=√5²+12²
АВ=13 (см)
Ответ: 13 см и 120 см².
Дано: ABCD - ромб
АC и ВD – диагонали
АС=24см, ВD=10см
Найти: SABCD, АВ
Решение:
Слайд 17 О теореме Пифагора
Пребудет вечной истина, как скоро
Все
познает слабый человек! И ныне теорема Пифагора Верна, как и в его
далекий век. Обильно было жертвоприношенье Богам от Пифагора. Сто быков Он отдал на закланье и сожженье За света луч, пришедший с облаков. Поэтому всегда с тех самых пор, Чуть истина рождается на свет, Быки ревут, ее почуя, вслед. Они не в силах свету помешать, А могут лишь закрыв глаза дрожать От страха, что вселил в них Пифагор.A.Шамиссо
Слайд 18 «Сегодня на уроке я повторил…»
«Сегодня на уроке я узнал…»
«Сегодня
на уроке я научился…»
ИТОГ УРОКА
