Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Золотое сечение 6 класс
Содержание
- 1. Золотое сечение 6 класс
- 2. Золотое сечение (золотая пропорция)— деление непрерывной величины
- 3. Термин «золотое сечение» (goldener Schnitt) был введён в обиход Мартином Омом в 1835 году.
- 4. Золотое сечение отрезка AB можно
- 5. Отрезав квадрат от прямоугольника, построенного по принципу
- 6. Каждый конец пятиугольной звезды представляет собой золотой
- 7. Пифагор – древнегреческий философ и математикVl в. до н. э.Первый ввёл понятие золотого сечения
- 8. Пирамида Хеопса площадь боковой поверхности Пирамиды относится
- 9. Слайд 9
- 10. Гробница Тутанхамона
- 11. Ряд ФибоначчиС историей золотого сечения косвенным образом
- 12. ЕвклидПрименил золотое сечениесоздавая геометрию
- 13. ПлатонРассказывал, что Вселенная устроена согласно золотому сечению
- 14. АристотельНашёл соответствие золотого сечения этическому закону
- 15. Лука Пачоли1509 издал книгу «Божественная пропорция»
- 16. Слайд 16
- 17. 1 побег- 100ед.2 – 62 ед.3- 38
- 18. Яйцо птицы имеет золотые пропорцииДлинна хвоста ящерицы
- 19. Гёте Подчёркивал тенденцию природы к спиральности
- 20. Спирали вЖивой природе1,6180339887…
- 21. Слайд 21
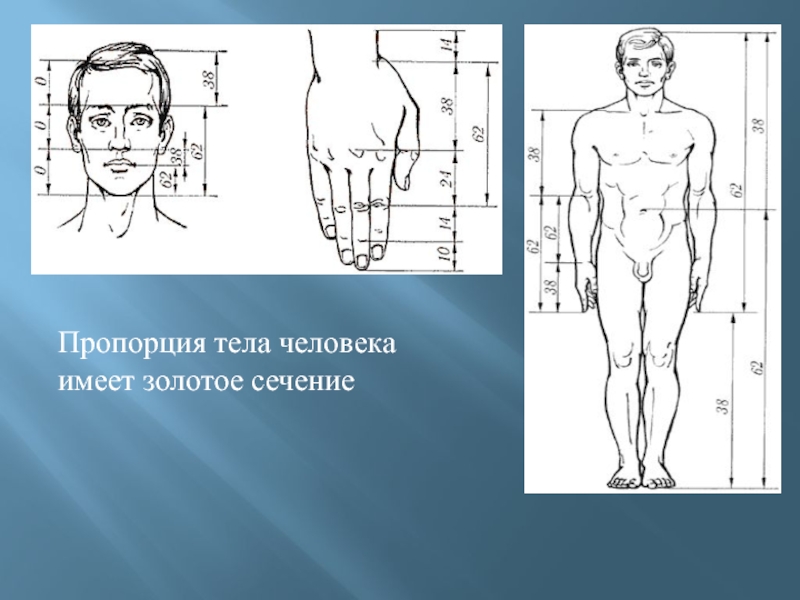
- 22. Пропорция тела человека имеет золотое сечение
- 23. Золотое сечение в скульптуре
- 24. Знаменитая статуя Аполлона Бельведерского
- 25. Скульптор Фидий Использовал золотое сечение в статуях
- 26. Золотое сечение в архитектуре
- 27. Парфенон V в. до н. э.
- 28. Пантеон
- 29. Здание сената в КремлеАрхитектор М. Казаков
- 30. Первая клиническая больница ПироговаАрхитектор М. Казаков
- 31. Дом ПашковаАрхитектор Бажов
- 32. Золотое сечение в живописи
- 33. Леонардо да ВинчиПортрет Монны Лизы
- 34. Слайд 34
- 35. Слайд 35
- 36. Слайд 36
- 37. Слайд 37
- 38. Форма, в основе построения которой лежат сочетание
- 39. Золотое сечение в музыке
- 40. Л.Л. Сабанеев
- 41. Аренский
- 42. "В геометрии существует два сокровища - теорема
- 43. Спасибо за внимание!
- 44. Скачать презентанцию
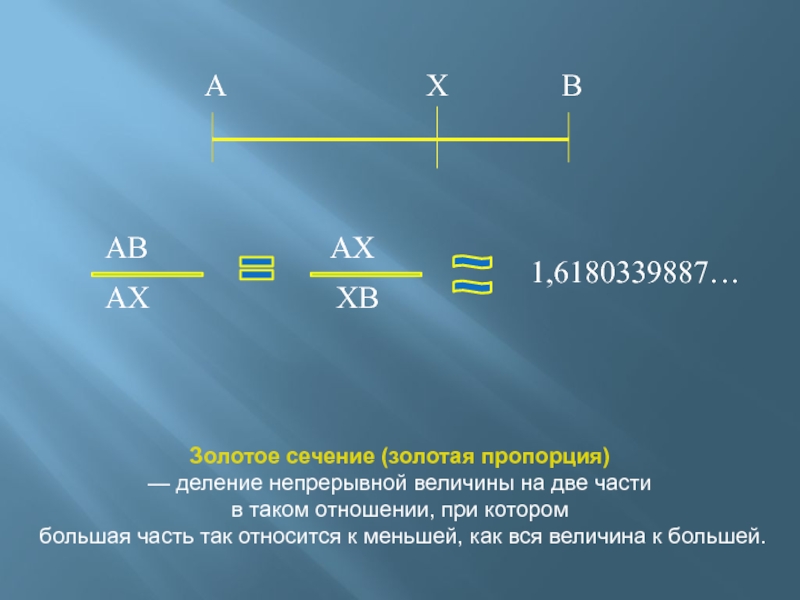
Золотое сечение (золотая пропорция)— деление непрерывной величины на две части в таком отношении, при котором большая часть так относится к меньшей, как вся величина к большей.
Слайды и текст этой презентации
Слайд 1Золотое
сечение
Презентацию выполнил
учащийся 6 «А» класса
МОУ СОШ № 5 г. Кстово
Красильников
Владимир
Слайд 2Золотое сечение (золотая пропорция)
— деление непрерывной величины на две части
в таком отношении, при котором
большая часть так относится к
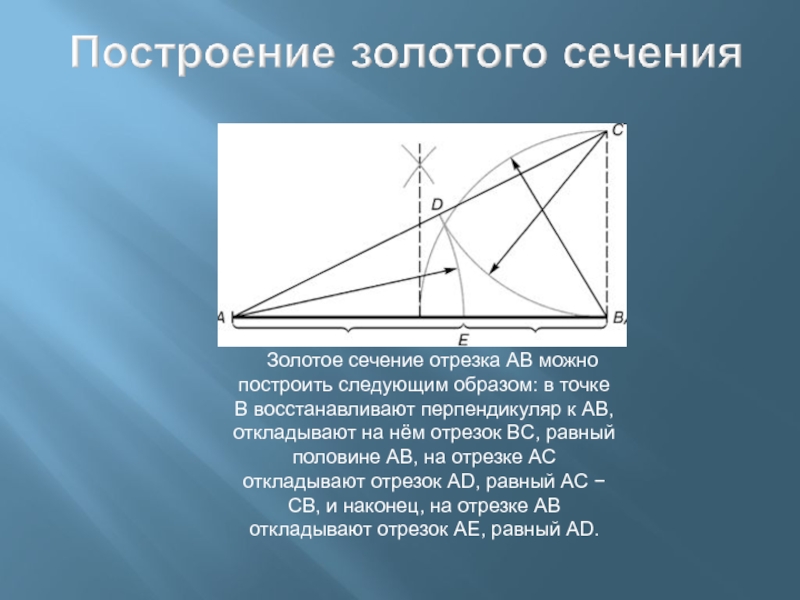
меньшей, как вся величина к большей.Слайд 4 Золотое сечение отрезка AB можно построить следующим образом:
в точке B восстанавливают перпендикуляр к AB, откладывают на нём
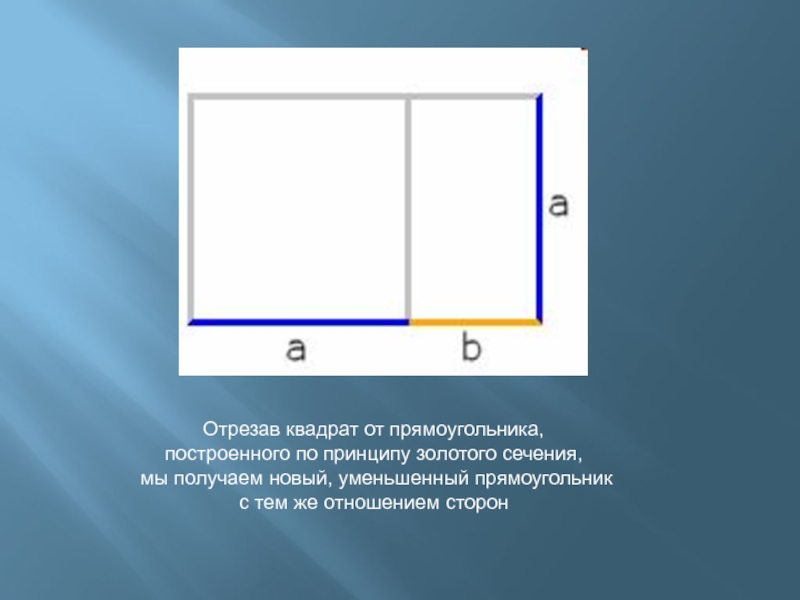
отрезок BC, равный половине AB, на отрезке AC откладывают отрезок AD, равный AC − CB, и наконец, на отрезке AB откладывают отрезок AE, равный AD.Слайд 5Отрезав квадрат от прямоугольника,
построенного по принципу золотого сечения,
мы
получаем новый, уменьшенный прямоугольник
с тем же отношением сторон
Слайд 6Каждый конец пятиугольной звезды
представляет собой золотой треугольник.
Его стороны
образуют угол 36° при вершине,
а основание, отложенное на боковую
сторону, делит ее в пропорции золотого сечения.
Слайд 7Пифагор – древнегреческий философ и математик
Vl в. до н. э.
Первый
ввёл понятие золотого сечения
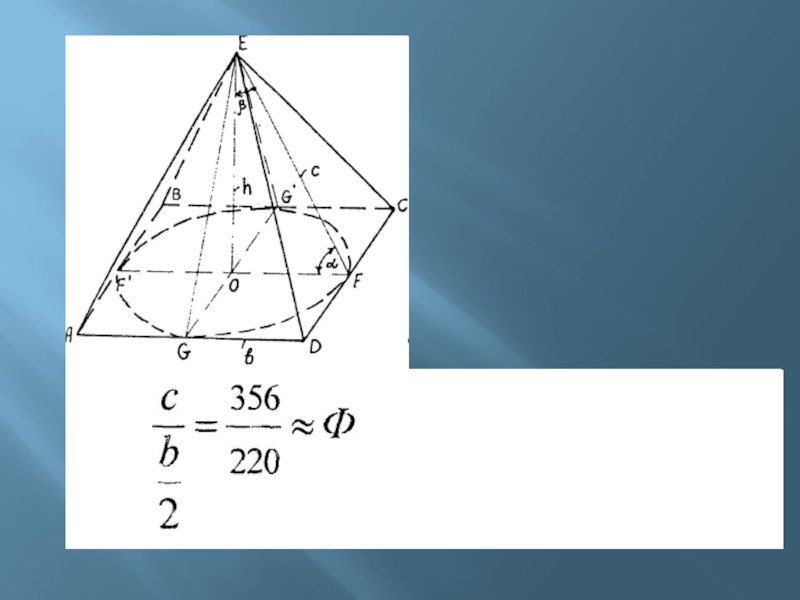
Слайд 8Пирамида Хеопса
площадь боковой поверхности Пирамиды относится к площади основания,
как площадь полной поверхности Пирамиды к площади боковой поверхности.
Слайд 11Ряд Фибоначчи
С историей золотого сечения косвенным образом связано имя итальянского
математика монаха Леонардо из Пизы, более известного под именем Фибоначчи
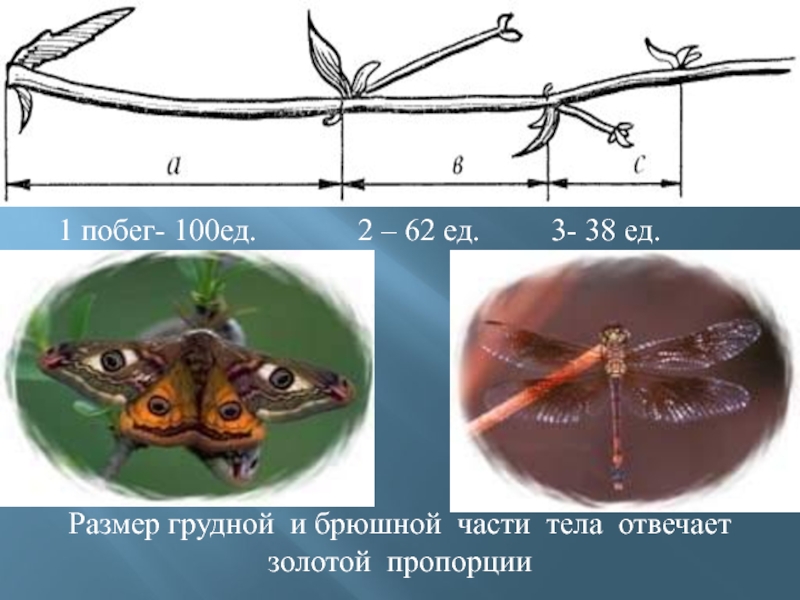
(сын Боначчи). Он много путешествовал по Востоку, познакомил Европу с индийскими (арабскими) цифрами. В 1202 г вышел в свет его математический труд «Книга об абаке» (счетной доске), в котором были собраны все известные на то время задачи. Одна из задач гласила «Сколько пар кроликов в один год от одной пары родится». Размышляя на эту тему, Фибоначчи выстроил такой ряд чисел 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 и т.д. известен как ряд Фибоначчи. Особенность последовательности чисел состоит в том, что каждый ее член, начиная с третьего, равен сумме двух предыдущих 2 + 3 = 5; 3 + 5 = 8; 5 + 8 = 13, 8 + 13 = 21; 13 + 21 = 34 и т.д., а отношение смежных чисел ряда приближается к отношению золотого деления. Так, 21 : 34 = 0,617, а 34 : 55 = 0,618.Слайд 171 побег- 100ед.
2 – 62 ед.
3- 38 ед.
Размер грудной и
брюшной части тела отвечает
золотой пропорции
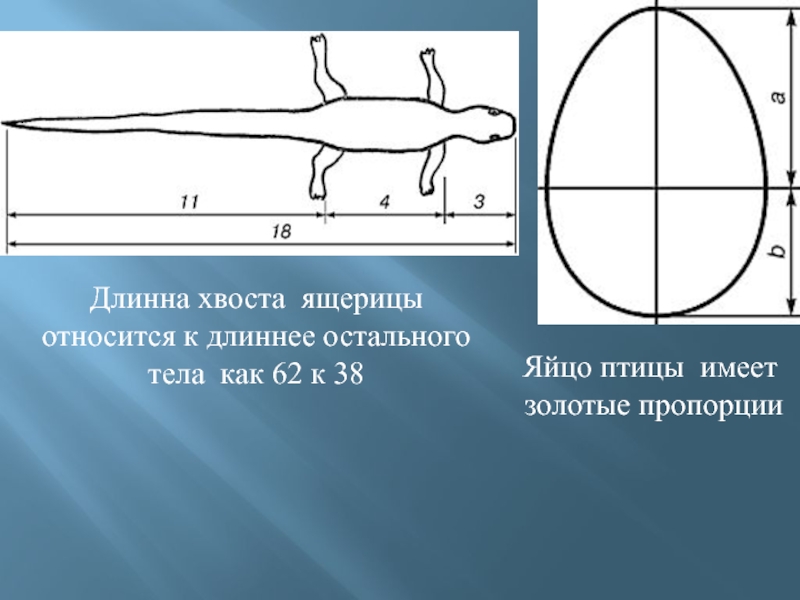
Слайд 18Яйцо птицы имеет
золотые пропорции
Длинна хвоста ящерицы относится к длиннее
остального тела как 62 к 38
Слайд 38Форма, в основе построения которой лежат сочетание симметрии и золотого
сечения, способствует наилучшему зрительному восприятию и появлению ощущения красоты и
гармонии.Слайд 41Аренский
Бетховен
Бородин ГайднМоцарт Скрябин Шопен Шуберт
90% всех их произведений - Золотое сечение
Слайд 42"В геометрии существует два сокровища - теорема Пифагора и деление
отрезка в крайнем и среднем отношении. Первое можно сравнить с
ценностью золота, второе можно назвать драгоценным камнем".астроном Иоганн Кеплер