Презентация для занятия по теме "Функция нескольких переменных"

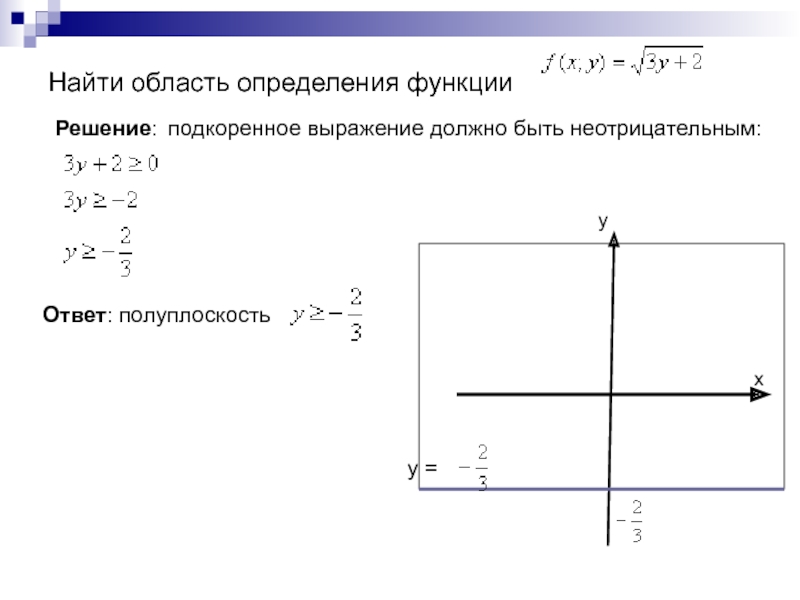
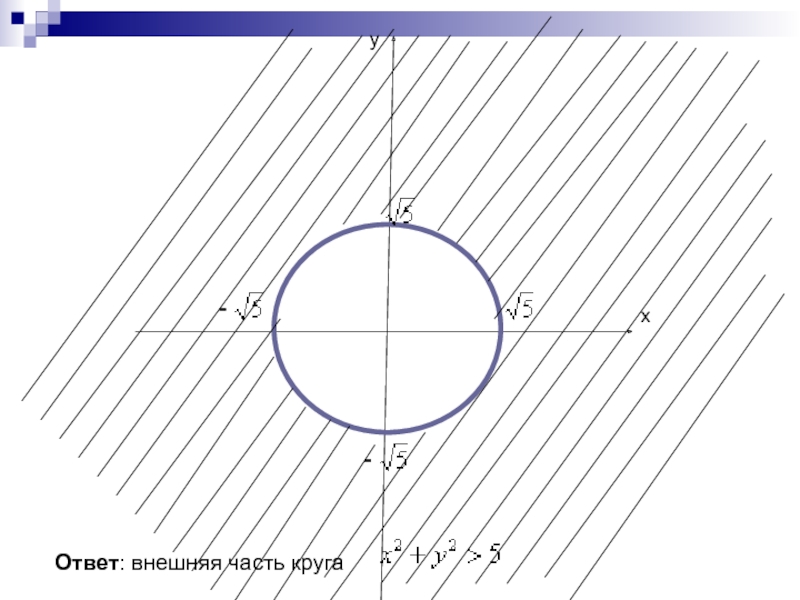
системе значений x,y,z,…,t, из области их изменений (области определения),
соответствует

определенное значение u.

Областью определения функции называется совокупность всех точек, в которых она имеет определенные действительные значения.

Для функции двух переменных z=f(x,y) область определения представляет некоторую совокупность точек плоскости, а для функции трех переменных
u = f (x,y,z) –некоторую совокупность точек пространства.

Функция n переменных.

 либо z= f(x,y) ,
или же другой стандартной буквой: u=f(x,y)

, u = u (x,y)

Функцией двух переменных называется закон,
по которому каждой паре значений независимых переменных x,y  (аргументов) из области определения соответствует значение зависимой переменной  z (функции).

переменной                соответствует определённая линия на плоскости

(например,                        – всем знакомая школьная парабола), то график функции двух переменных                                     располагается в трёхмерном пространстве.
На практике чаще всего приходится иметь дело с поверхностью, но иногда график функции может представлять собой, например, пространственную прямую (прямые) либо даже единственную точку.

, для которых существует значение     .


Графически область определения

представляет собой всю плоскость            либо её часть.
Так, областью определения функции                                является вся координатная

плоскость           – по той причине, что для любой точки            существует значение    .

особое внимание на те функции, в которых есть дроби, корни

чётной степени, логарифмы и т. д. 

может обращаться в ноль, то:
Ответ: вся координатная плоскость                    

 
кроме точек, принадлежащих прямой                              

y

x

5

5

0

Ответ: полуплоскость                          
у
x

y =