Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация к уроку алгебры в 11 классе по теме: "Логарифм"
Содержание
- 1. Презентация к уроку алгебры в 11 классе по теме: "Логарифм"
- 2. Свойства и формулы логарифмированияОсновные свойства логарифмической функцииГрафик логарифмической функцииСпособы решения логарифмических уравненийРешение неравенствИстория логарифмовЗаключениеВещественный логарифмПонятие логарифма
- 3. Вычисление логарифма называется логарифмированием. Нахождение
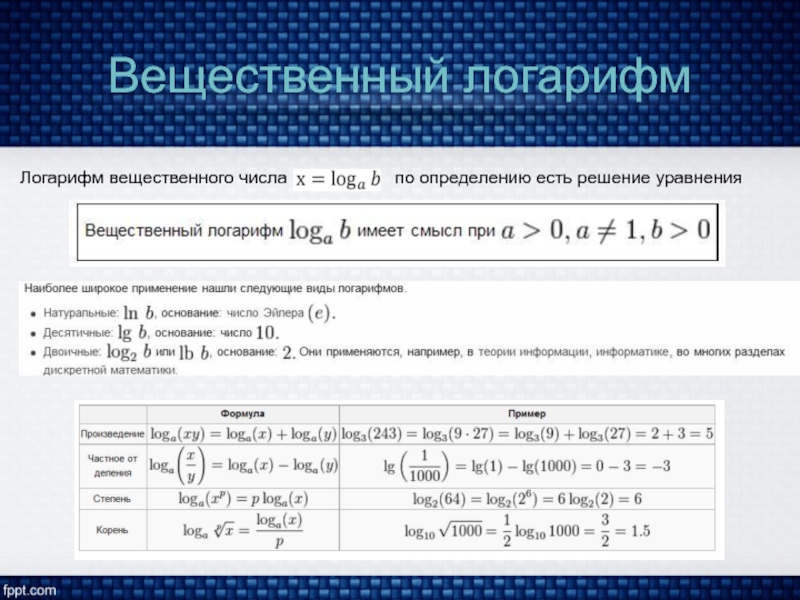
- 4. Вещественный логарифмЛогарифм вещественного числапо определению есть решение уравнения
- 5. Свойства и формулы логарифмированияОсновное логарифмическое тождество
- 6. Основные свойства логарифмической функции
- 7. График логарифмической функцииЛогарифмическая функция обратна к показательнойГрафики логарифмических функций
- 8. Способы решения логарифмических уравнений 1.По определению логарифма
- 9. Способы решения логарифмических уравнений 2.По свойствам логарифмов и логарифмической функции
- 10. Способы решения логарифмических уравнений 3.Введение новой переменной
- 11. Способы решения логарифмических уравнений 4.Графический способ
- 12. Способы решения логарифмических уравнений 5.Введение новой переменной
- 13. Решение неравенств
- 14. Решение неравенств
- 15. В 1614 году шотландский математик-любитель Джон Непер
- 16. «Я всегда старался, насколько позволяли мои силыи
- 17. Скачать презентанцию
Свойства и формулы логарифмированияОсновные свойства логарифмической функцииГрафик логарифмической функцииСпособы решения логарифмических уравненийРешение неравенствИстория логарифмовЗаключениеВещественный логарифмПонятие логарифма
Слайды и текст этой презентации
Слайд 1
Презентация
по теме : «Логарифмы»
Автор:
учитель математики ДОШ № 55
Русанова
Галина Николаевна
Слайд 2
Свойства и формулы логарифмирования
Основные свойства логарифмической функции
График логарифмической функции
Способы решения
логарифмических уравнений
Решение неравенств
История логарифмов
Заключение
Вещественный логарифм
Понятие логарифма
Слайд 3
Вычисление логарифма называется логарифмированием.
Нахождение
равносильно решению уравнения
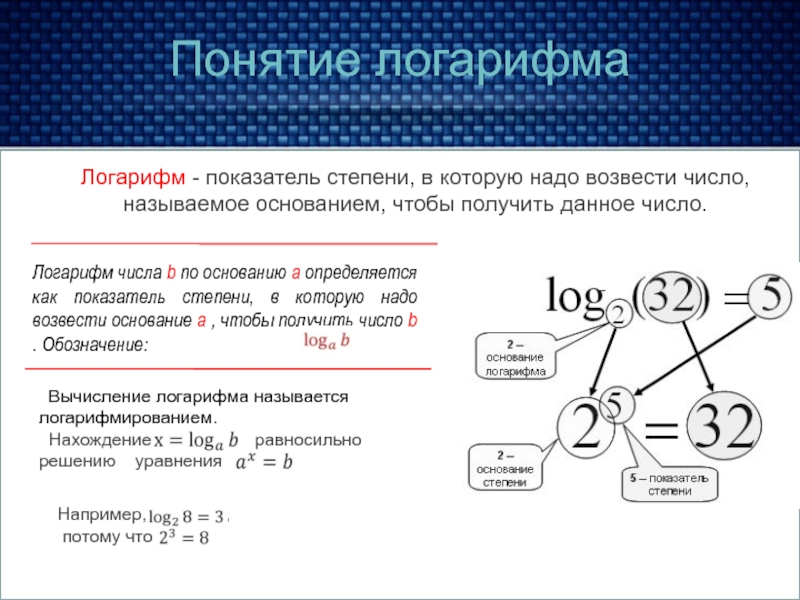
.Логарифм числа b по основанию a определяется как показатель степени, в которую надо возвести основание a , чтобы получить число b . Обозначение:
Например, ,
потому что ..
Понятие логарифма
Логарифм - показатель степени, в которую надо возвести число, называемое основанием, чтобы получить данное число.
Слайд 7
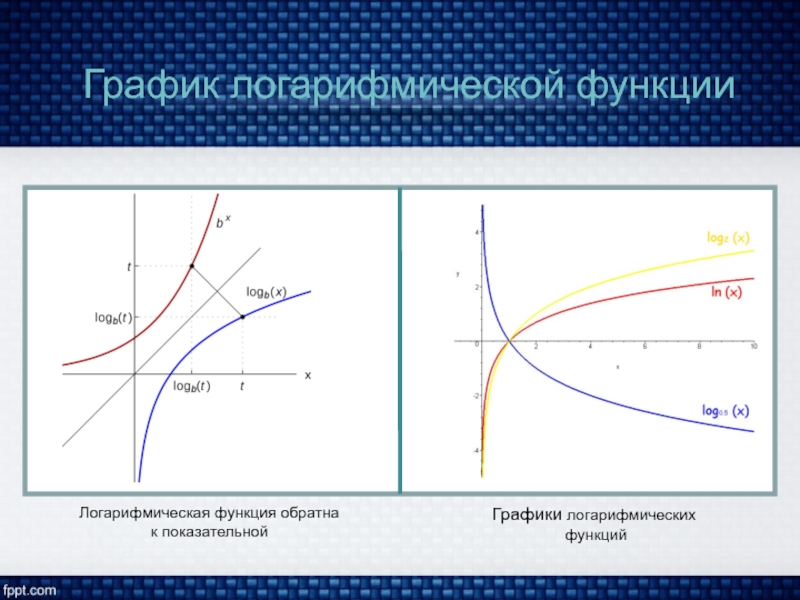
График логарифмической функции
Логарифмическая функция обратна к показательной
Графики логарифмических
функций
Слайд 9
Способы решения логарифмических уравнений
2.По свойствам логарифмов и
логарифмической функции
Слайд 15В 1614 году шотландский математик-любитель Джон Непер опубликовал на латинском
языке сочинение под названием «Описание удивительной таблицы логарифмов» Термин логарифм,
предложенный Непером, утвердился в науке.Спустя несколько лет после книги Непера появились логарифмические таблицы, использующие более близкое к современному понимание логарифма. Лондонский профессор Генри Бригс издал 14-значные таблицы десятичных логарифмов (1617)
Появление логарифмов оказало сильное влияние на многие математические концепции, в том числе:
Исторический аспект
Формирование и признание общего понятия иррациональных и трансцендентных чисел.
Появление показательной функции и общего понятия числовой функции, числа Эйлера, развитие теории разностных уравнений.
Начало работы с бесконечными рядами.
Общие методы решения дифференциальных уравнений различных типов.
Существенное развитие теории численных методов, требуемых для вычисления точных логарифмических таблиц.
Слайд 16
«Я всегда старался, насколько позволяли мои силы
и способности, избавиться от
трудности и скуки
вычислений, докучливость которых обыкновенно
отпугивает очень многих от изучения
математики.»Джон Непер
