Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация к уроку геометрии по теме "Теорема Пифагора"
Содержание
- 1. Презентация к уроку геометрии по теме "Теорема Пифагора"
- 2. Содержание Формулировка теоремы Доказательства теоремы Значение теоремы Пифагора
- 3. Формулировка теоремы« Доказать, что квадрат, построенный
- 4. Современная формулировка« В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов».
- 5. Доказательства теоремы На данный момент в научной
- 6. Векторное доказательство теоремыРассмотрим треугольник ABC
- 7. Пусть АВС - прямоугольный треугольник
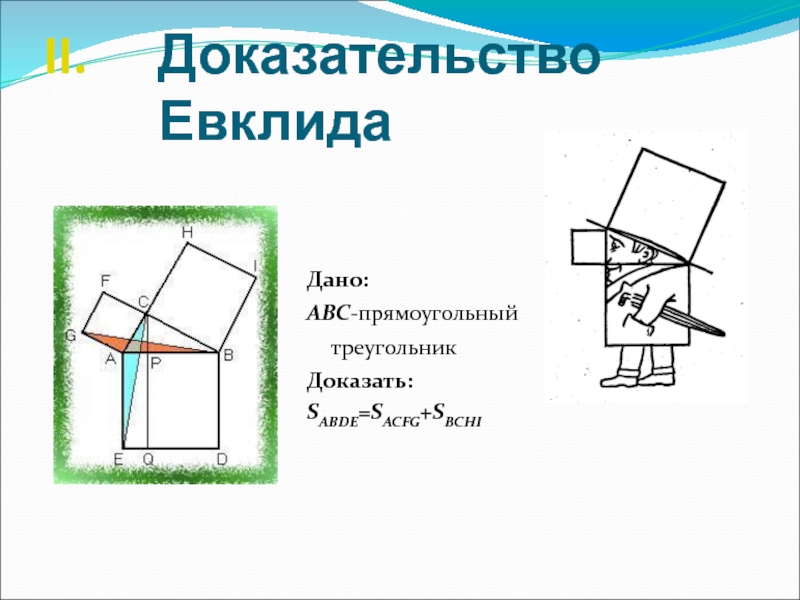
- 8. Доказательство Евклида Дано: ABC-прямоугольный треугольник Доказать:SABDE=SACFG+SBCHI
- 9. Доказательство: Пусть ABDE-квадрат, построенный на гипотенузе прямоугольного
- 10. Очевидно, что углы CAE=GAB(=A+90°); отсюда следует, что
- 11. Алгебраическое доказательствоДано: ABC-прямоугольный треугольникДоказать: AB2=AC2+BC2 Доказательство: 1) Проведем высоту
- 12. Геометрическое доказательство Дано: ABC-прямоугольный треугольникДоказать: BC2=AB2+AC2Доказательство: 1) Построим
- 13. Значение теоремы ПифагораТеорема Пифагора- это одна
- 14. Уделом истины не может быть забвенье,
- 15. Доказательство теоремы Пифагора учащиеся средних веков считали
- 16. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Теорема Пифагора
Пребудет вечной истина, как скоро
Её познает слабый человек!
И ныне
теорема Пифагора
Слайд 3Формулировка
теоремы
« Доказать, что квадрат, построенный на гипотенузе прямоугольного треугольника,
равновелик сумме квадратов, построенных на катетах»
« Площадь квадрата, построенного
на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах». Во времена Пифагора теорема звучала так:
или
Слайд 4Современная формулировка
« В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов
катетов».
Слайд 5Доказательства теоремы
На данный момент в научной литературе зафиксировано 367
доказательств данной теоремы (геометрических, алгебраических, механических и т.д.).
Слайд 7
Пусть АВС - прямоугольный треугольник с прямым углом при вершине
С, построенный на векторах. Тогда справедливо векторное равенство: b +
c = a откуда имеем c = a - b возводя обе части в квадрат, получим c²=a²+b²-2ab Так как a перпендикулярно b, то ab=0, откуда c²=a²+b² или c²=a²+b²Таким образом, теорема Пифагора снова доказана.
Слайд 9Доказательство:
Пусть ABDE-квадрат, построенный на гипотенузе прямоугольного треугольника ABC, а
ACFG и BCHI-квадраты, построенные на его катетах. Опустим из вершины
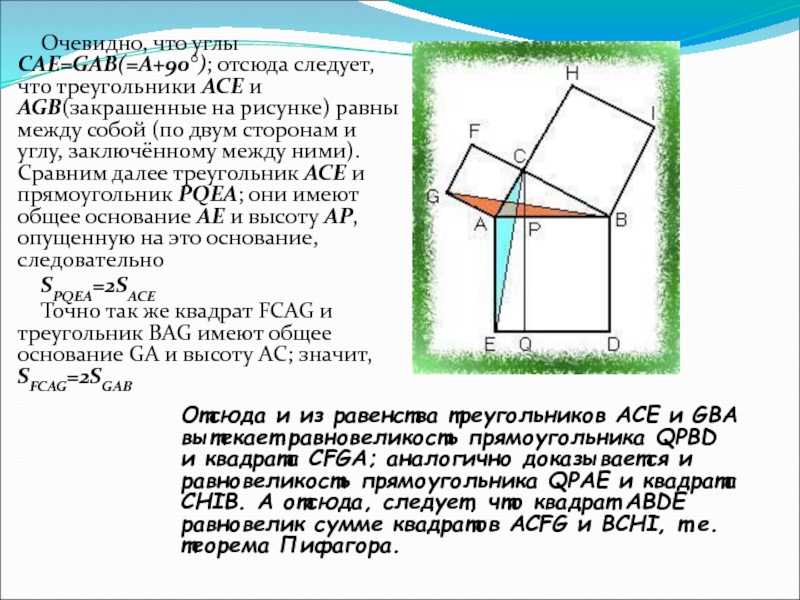
C прямого угла перпендикуляр CP на гипотенузу и продолжим его до пересечения со стороной DE квадрата ABDE в точке Q; соединим точки C и E, B и G.Слайд 10Очевидно, что углы CAE=GAB(=A+90°); отсюда следует, что треугольники ACE и
AGB(закрашенные на рисунке) равны между собой (по двум сторонам и
углу, заключённому между ними). Сравним далее треугольник ACE и прямоугольник PQEA; они имеют общее основание AE и высоту AP, опущенную на это основание, следовательноSPQEA=2SACE
Точно так же квадрат FCAG и треугольник BAG имеют общее основание GA и высоту AC; значит, SFCAG=2SGAB
Отсюда и из равенства треугольников ACE и GBA вытекает равновеликость прямоугольника QPBD и квадрата CFGA; аналогично доказывается и равновеликость прямоугольника QPAE и квадрата CHIB. А отсюда, следует, что квадрат ABDE равновелик сумме квадратов ACFG и BCHI, т.е. теорема Пифагора.
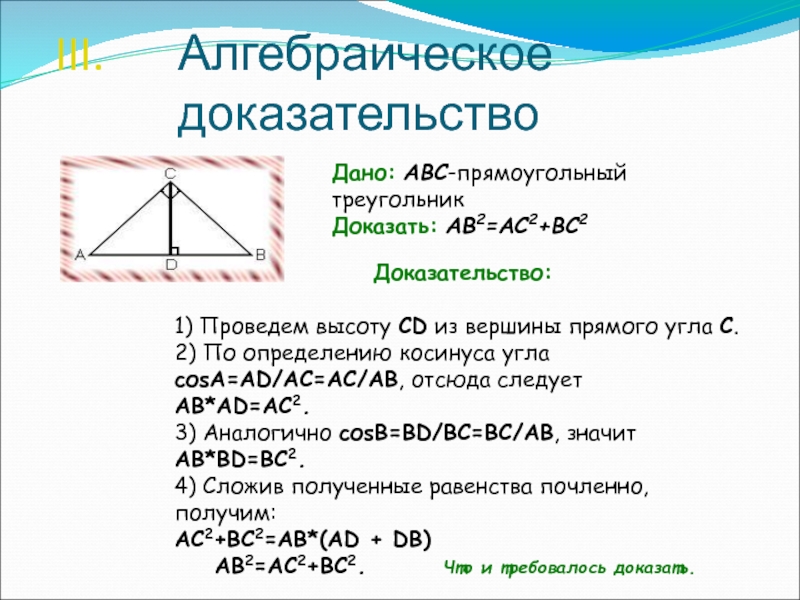
Слайд 11Алгебраическое доказательство
Дано: ABC-прямоугольный треугольник
Доказать: AB2=AC2+BC2
Доказательство:
1) Проведем высоту CD из вершины прямого
угла С.
2) По определению косинуса угла соsА=AD/AC=AC/AB, отсюда следует
AB*AD=AC2.
3) Аналогично соsВ=BD/BC=BC/AB,
значит AB*BD=BC2.
4) Сложив полученные равенства почленно, получим:
AC2+BC2=АВ*(AD + DB)
AB2=AC2+BC2. Что и требовалось доказать.
Слайд 12Геометрическое доказательство
Дано: ABC-прямоугольный треугольник
Доказать: BC2=AB2+AC2
Доказательство:
1) Построим отрезок CD равный отрезку
AB на продолжении катета AC прямоугольного треугольника ABC. Затем опустим
перпендикуляр ED к отрезку AD, равный отрезку AC, соединим точки B и E. 2) Площадь фигуры ABED можно найти, если рассматривать её как сумму площадей трёх треугольников:SABED=2*AB*AC/2+BC2/2
3) Фигура ABED является трапецией, значит, её площадь равна:
SABED= (DE+AB)*AD/2.
4) Если приравнять левые части найденных выражений, то получим:
AB*AC+BC2/2=(DE+AB)(CD+AC)/2
AB*AC+BC2/2= (AC+AB)2/2
AB*AC+BC2/2= AC2/2+AB2/2+AB*AC
BC2=AB2+AC2.
Это доказательство было опубликовано в 1882 году Гэрфилдом.
Слайд 13 Значение теоремы Пифагора
Теорема Пифагора- это одна из самых важных
теорем геометрии. Значение её состоит в том, что из неё
или с её помощью можно вывести большинство теорем геометрии.Слайд 14 Уделом истины не может быть забвенье, Как только мир ее
увидит взор; И теорема та, что дал нам Пифагор, Верна
теперь, как в день ее рожденья. За светлый луч с небес вознес благодаренье Мудрец богам не так, как было до тех пор. Ведь целых сто быков послал он под топор, Чтоб их сожгли как жертвоприношенье. Быки с тех пор, как только весть услышат, Что новой истины уже следы видны, Отчаянно мычат и ужаса полны: Им Пифагор навек внушил тревогу. Не в силах преградить той истине дорогу Они, закрыв глаза, дрожат и еле дышат.А. фон Шамиссо
(Перевод А. Хованского)