Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Математика и законы красоты
Содержание
- 1. Математика и законы красоты
- 2. С давних пор человек стремится окружать себя
- 3. Математика – царица всех наук, символ мудрости.
- 4. Гармония – она означает «согласованность, соразмерность, единство
- 5. Красота – она многогранна и многолика. Она
- 6. Однако не стоит наводить «математический» порядок в
- 7. В существующих формулах эстетической привлекательности математического объекта
- 8. Например пифагорейский музыкальный строй, определивший на столетия
- 9. Наряду с математической теорией музыки существует математическая
- 10. Велика роль пропорций в архитектуре. Пропорции в
- 11. Одним из основополагающих принципов красоты является симметрия.
- 12. Симметрия определяется как "красота, обусловленная пропорциональностью частей
- 13. Очень важно найти математические закономерности в прекрасном
- 14. Скачать презентанцию
С давних пор человек стремится окружать себя красивыми вещами. Уже предметы обихода жителей древности, которые, казалось бы, преследовали практические цели – служить хранилищем воды, оружием на охоте и т. д. демонстрируют
Слайды и текст этой презентации
Слайд 2С давних пор человек стремится окружать себя красивыми вещами. Уже
предметы обихода жителей древности, которые, казалось бы, преследовали практические цели
– служить хранилищем воды, оружием на охоте и т. д. демонстрируют стремление человека к красоте.
Слайд 3Математика – царица всех наук, символ мудрости. Красота математики среди
наук недосягаема, а красота является одним из связующих звеньев науки
и искусства. Это не только стройная система законов, теорем и задач, но и уникальное средство познания красоты.
Слайд 4Гармония – она означает «согласованность, соразмерность, единство частей и целого,
обуславливающие внутреннюю и внешнюю формы предмета, события, явления, их совершенство».
Внешне гармония может проявляться в мелодии, ритме, симметрии, пропорциональности.
Слайд 5Красота – она многогранна и многолика. Она выражает высшую целесообразность
устройства мира, подтверждает универсальность математических закономерностей, которые действуют одинаково эффективно
в кристаллах, живых организмах, в атоме и во Вселенной, в произведениях искусства и в научных открытиях.
Слайд 6Однако не стоит наводить «математический» порядок в искусстве. Оно живет
своей жизнью, оно состоит из противоположных начал – материального и
духовного, рационального и иррационального, сконструированного и сотворенного, рассчитанного и угаданного. В первом случае искусство доступно точному математическому анализу, во втором не подвластно математике, да и не нужно разрушать эту волшебную часть искусства логикой.
Слайд 7В существующих формулах эстетической привлекательности математического объекта красота его обусловлена
взаимодействием его обобщенного образа, созданного нашей психикой, и оригинальности, выделяющей
этот объект из множества других.
Слайд 8Например пифагорейский музыкальный строй, определивший на столетия судьбу европейской музыки
– это математика. В 18в. создается музыкальная акустика. После создания
точной математической теории струны, поняв, что любой музыкальный инструмент – всего-навсего «физико-акустический прибор», судьба музыки уже не отделима от математики.
Слайд 9Наряду с математической теорией музыки существует математическая теория живописи. Это
теория перспективы, представляющая, по словам Леонардо да Винчи, «тончайшее исследование
и изобретение, основанное на изучении математики, которое силою линий заставляло казаться отдаленным то, что близко, и большим то, что невелико».
Слайд 10Велика роль пропорций в архитектуре. Пропорции в архитектуре – это
как бы ее внутренняя красота. Она невидима непосредственно, но всегда
ощутима, подобно красоте духовной. Не менее важна роль геометрии в архитектуре. Только неотступно следуя законам геометрии, архитекторы древности могли создавать свои шедевры.
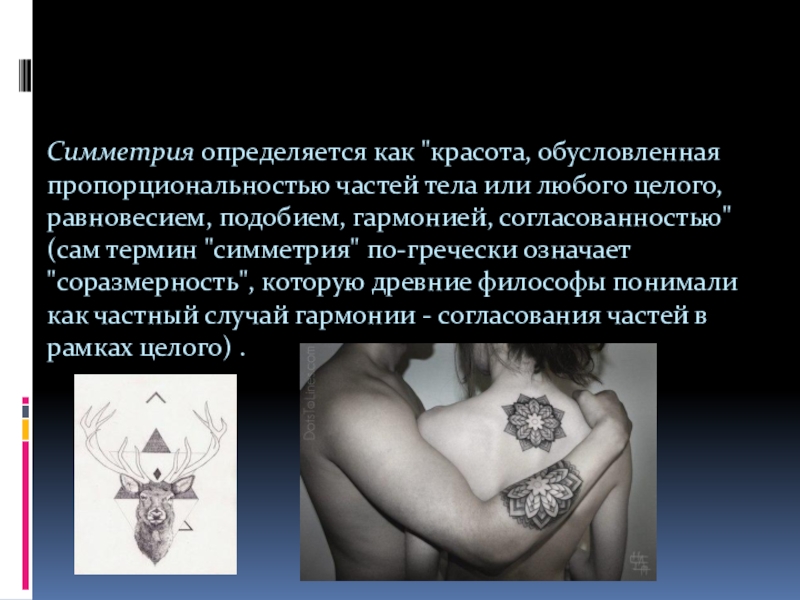
Слайд 12Симметрия определяется как "красота, обусловленная пропорциональностью частей тела или любого
целого, равновесием, подобием, гармонией, согласованностью" (сам термин "симметрия" по-гречески означает
"соразмерность", которую древние философы понимали как частный случай гармонии - согласования частей в рамках целого) .
Слайд 13Очень важно найти математические закономерности в прекрасном – «законы красоты».
Попытки хотя бы приблизится к ним предпринимались с древнейших времен:
это и математические законы Пифагора в музыке, и геометрическая модель вселенной Кеплера, это и система пропорций в скульптуре и архитектуре, и геометрические законы живописи. И сегодня энтузиазм исследователей не убывает.
