Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
История возникновения интеграла
Содержание
- 1. История возникновения интеграла
- 2. Архимед определил длину окружности и площадь круга,
- 3. Понятие интеграла и интегральное
- 4. Слайд 4
- 5. 1612 г. был для жителей австрийского города
- 6. В отличие от Кеплера автор «Геометрии неделимых»,
- 7. Среди последователей Кавальери самыми
- 8. Большой вклад в развитие интегрального исчисления внес
- 9. Еще более четкое понятие определенного интеграла выступает
- 10. С основными достижения в математике XVII в.
- 11. Скачать презентанцию
Архимед определил длину окружности и площадь круга, объем и поверхности шара.При этом Архимед разработал и применил методы, предвосхитившие созданное в XVII в. интегральное исчисление.
Слайды и текст этой презентации
Слайд 1История возникновения интеграла
Работу выполнила:
Ученица 10 класса
Сотникова Галина
Учитель: Зырина Н.Л.
2012 год
Слайд 2Архимед определил длину окружности и площадь круга, объем и поверхности
шара.
XVII в. интегральное исчисление.Слайд 3 Понятие интеграла и интегральное исчисление возникли из
потребности вычислять площади любых фигур и поверхностей , объемы произвольных
тел.Предыстория интегрального исчисления выходит к глубокой древности.
Идея интегрального исчисления была древними учеными предвосхищена гораздо в большой мере, чем идея дифференциального исчисления.
Слайд 4 Первые
значительные попытки развития интеграционных методов Архимеда, увенчавшиеся успехом , были
предприняты в XVII в.., когда, с одной стороны, были достигнуты значительные успехи в области алгебры, а с другой – все более интенсивно развивались экономика, естествознание и техника, требовавшие более общих и мощных математических методов изучения и вычисления величин. Одним из первых видных ученых XVII в.., стремившихся к возрождению и развитию интеграционных метода Архимеда, был Иоганн Кеплер, открывший законы движения планет. Кеплер вычислял площади плоских фигур и поверхностей , объемы тел, основываясь на идее разложения фигур и тел на бесконечное число бесконечно малых частей, которые он называл «тончайшими кружочками» или «частями крайней малой ширины»; из этих мельчайших частиц, суммированныхим, он составляет фигуру, эквивалентную
первоначальной, но площадь или объем которой
ему известен.
Слайд 51612 г. был для жителей австрийского города Линца, в котором
жил тогда Кеплер, и его окрестностей исключительно урожайным, особенно изобиловал
виноград. Люди заготовляли винные бочки и хотели знать, как практически определять их объемы. Этот вопрос как раз и входил в круг идей, которыми интересовался Кеплер. Так родилась его «Новая стереометрия винных бочек», вышедшая в свет в 1615г.Слайд 6В отличие от Кеплера автор «Геометрии неделимых», Кавальери, считал свои
«неделимые», линии и плоскости лишенными всякой толщины. Под термином «все
линии» какой-либо плоскости фигуры Кавальери понимал все же сумму этих параллельных собой линии, из которых составлена фигура.Слайд 7 Среди последователей Кавальери самыми видными учеными, подготавливавшими
в XVII в., создание интегрального и дифференциального исчисления, завершенное Ньютоном
и Лейбницем, были Дж. Валлис., П. Ферма и Б. Паскаль.Методы Валлиса, изложенные в его «Арифметике бесконечных» (1655), развивались вслед за методом неделимых Кавальери. При этом Валлис исходит уже не из примитивного понятия всех линий, а из суммы. Он рассматривает площадь (определенный интеграл) как общий предел верхних и нижних интегральных сумм при описании и вписании ступенчатых фигур.
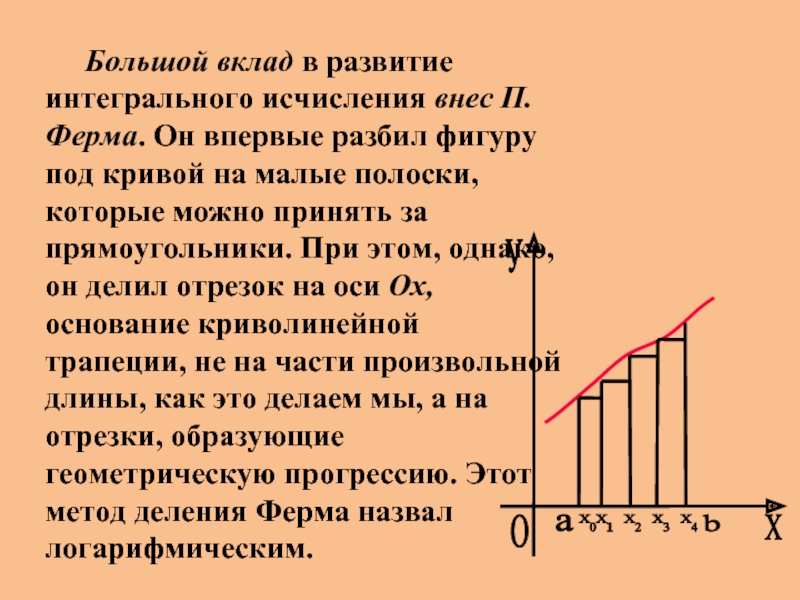
Слайд 8 Большой вклад в развитие интегрального исчисления внес П.Ферма. Он впервые
разбил фигуру под кривой на малые полоски, которые можно принять
за прямоугольники. При этом, однако, он делил отрезок на оси Oх, основание криволинейной трапеции, не на части произвольной длины, как это делаем мы, а на отрезки, образующие геометрическую прогрессию. Этот метод деления Ферма назвал логарифмическим.Слайд 9Еще более четкое понятие определенного интеграла выступает в трудах Б.
Паскаля. Он впервые познакомился с неделимыми у Кавальери, о котором
отзывался с большой похвалой. Однако, несмотря на то что Паскаль пользовался термином «неделимые», он их понимает не так, как Кавальери. «Сумма ординат» для Паскаля – это уже не все линии, а сумма неограниченного числа прямоугольников, сторонами каждого из которых служили ордината и маленькие равные отрезки абсцисс.Признавая огромные заслуги Паскаля, следует, однако, отметить его «слабость»: он не пользовался новой символической алгеброй и не производил алгебраических выкладок.
Подобно древнегреческим математикам, он все
выражал словами. Вероятно, это обстоятельство
явилось одной из причин, из-за которых Паскаль был
лишен возможности создать тот новый общий
алгоритм исчисления бесконечных малых,
которые открыли Ньютон и Лейбниц.
Перевод К. Бальмонта.
Слайд 10С основными достижения в математике XVII в. Лейбниц познакомился в
начале 70-х годов этого столетия, когда под влиянием голландского ученого
Х. Гюйгенса изучил, кроме его работ, «Геометрию» Декарта, труды Кавальери, Валлиса, Паскаля и др.Ньютон к основным понятиям и к алгоритму исчисления бесконечно малых пришел в середине 60-х годов XVII в., когда двадцатилетний Лейбниц был студентом юридического факультета и математикой еще не занимался.
Ньютон и Лейбниц, самостоятельно, каждый своими математическими выкладками пришли к понятию определенного интеграла и вывели формулу
Это и есть так называемая теперь «Формула Ньютона - Лейбница», которая носит название «основной формулы интегрального исчисления». Она позволяет
сводить довольно сложное вычисление
определенных интегралов,
т.е. нахождение предела
интегральных сумм, к сравнительно
более простой операции отыскивания
первообразных.
Теги