Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация по математике "Квадратичная функция"
Содержание
- 1. Презентация по математике "Квадратичная функция"
- 2. Квадратный трехчлен
- 3. Квадратное уравнениеЕсли стоит задача, определить значения
- 4. Квадратный трехчленЕсли существуют действительные корни x1 и x2 некоторого квадратного уравнения, то соответствующий трёхчлен можно разложить на линейные множители: ax2 + bx + c = a(x − x1)(x − x2)
- 5. Квадратный трехчленКвадратный трёхчлен также можно представить в виде:
- 6. Квадратичная функцияКвадратичной функцией называется функция, заданная формулой y = f(x), где f(x) -
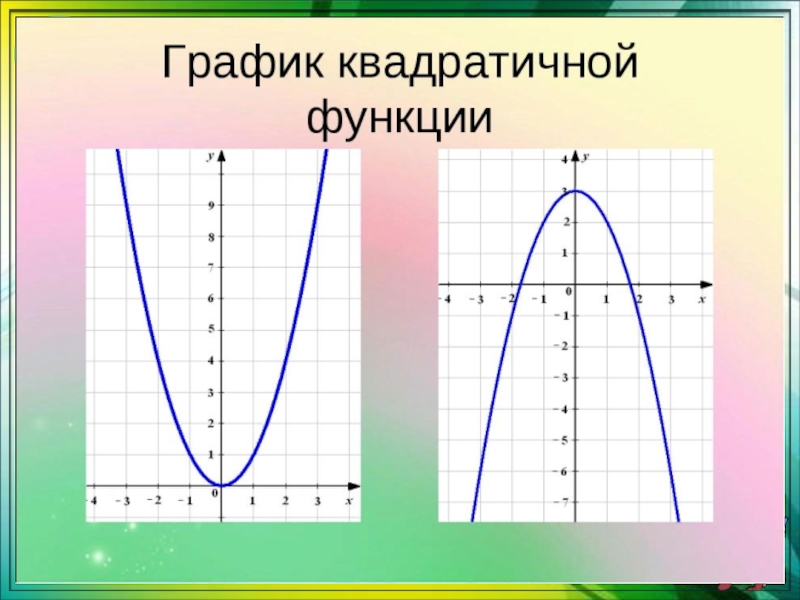
- 7. График квадратичной функцииГрафиком квадратичной функции является парабола, вершина которой находится в точке
- 8. Слайд 8
- 9. График квадратичной функцииПостроить эскиз графика квадратичной функции можно по
- 10. Свойства квадратичной функцииОбласть определения функции - вся
- 11. Свойства квадратичной функцииВ общем случае функция у
- 12. Свойства квадратичной функции
- 13. Свойства квадратичной функции
- 14. Построение графиков квадратичной функции онлайнhttps://umath.ru/calc/graph/?&func=sin(x);%20e%5Ex;http://www.yotx.ru/http://matematikam.ru/calculate-online/grafik.php https://graph.reshish.ru/
- 15. СПАСИБО ЗА ВНИМАНИЕ!!!
- 16. Скачать презентанцию
Квадратный трехчлен
Слайды и текст этой презентации
Слайд 3 Квадратное уравнение
Если стоит задача, определить значения переменной х, при которых
квадратный трёхчлен принимает нулевые значения, т.е. ax2 + bx + c = 0, то имеем квадратное уравнение.
ax2 + bx + c = 0
Слайд 4Квадратный трехчлен
Если существуют действительные корни x1 и x2 некоторого квадратного уравнения, то соответствующий трёхчлен можно
разложить на линейные множители:
ax2 + bx + c = a(x − x1)(x − x2)
Слайд 6Квадратичная функция
Квадратичной функцией называется функция, заданная формулой y = f(x), где f(x) - квадратный трёхчлен. Т.е.
формулой вида y = ax2 + bx + c, где a ≠ 0, b, c - любые действительные числа. Или преобразованной формулой
вида .Слайд 7График квадратичной функции
Графиком квадратичной функции является парабола, вершина которой находится в точке
Слайд 9График квадратичной функции
Построить эскиз графика квадратичной функции можно по характерным точкам.
Например, для
функции y = x2 берем точки
x 0 1 2 3
y 0 1 4 9
Соединяя их от руки, строим правую половинку
параболы. Левую получаем симметричным отражением относительно оси ординат.Слайд 10Свойства квадратичной функции
Область определения функции - вся числовая прямая: D(f)
= R = (−∞; ∞).
Область значений функции зависит от знака
коэффициента a. При a > 0 ветви параболы направлены вверх, функция имеет наименьшее (ymin), но не имеет наибольшего значения: E(f) = [ ymin; ∞); при a < 0 ветви параболы направлены вниз, функция имеет наибольшее (ymax), но не имеет наименьшего значения:E(f) = (−∞; ymax ].Слайд 11Свойства квадратичной функции
В общем случае функция у = ax2 +
bx + c не является ни четной, ни нечетной. Осью
симметрии параболы является прямая x = −b/2a. Функция будет четной только в случае, когда эта прямая совпадает с осью Oy, т.е. при b = 0.При a > 0 функция монотонно убывает на промежутке (−∞; −b/2a) и монотонно возрастает на промежутке (−b/2a; ∞). При a < 0 функция монотонно возрастает на промежутке (−∞; −b/2a) и монотонно убывает на промежутке (−b/2a; ∞).