Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация по теме "Тригонометрические функции. Функция у=sin x"
Содержание
- 1. Презентация по теме "Тригонометрические функции. Функция у=sin x"
- 2. Основные свойства функции.1. Область определения.2. Область изменения.3.
- 3. Функция y = sin xСвойства функции:1.
- 4. Функция y = sin xСвойства функции:
- 5. Функция y = sin xСвойства функции:4.
- 6. Функция y = sin xСвойства функции:5.
- 7. Функция y = sin xСвойства функции:6.
- 8. Доказательство. 1) При повороте точки вокруг начала
- 9. Функция y = sin xСвойства функции:
- 10. Функция y = sin xСвойства функции:8.
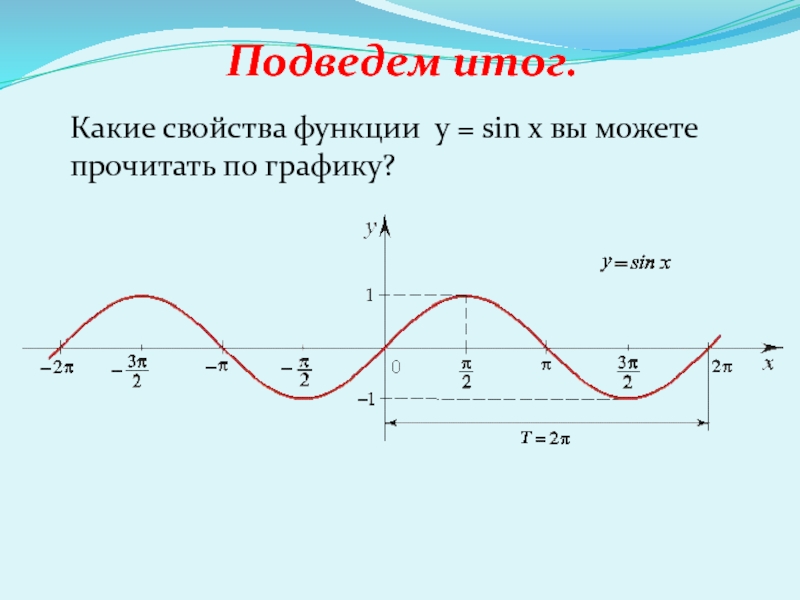
- 11. Какие свойства функции y = sin x вы можете прочитать по графику?Подведем итог.
- 12. Ресурсы:http://school.xvatit.comhttp://www.nado5.ru/e-book/trigonometricheskie-funkcii-i-ikh-grafikihttp://schoolife.ru/education/algebra/trigonometriya/trig-funkcii.html
- 13. Скачать презентанцию
Основные свойства функции.1. Область определения.2. Область изменения.3. Периодичность.4. Четность, нечетность.5. Нули функции.6. Промежутки возрастания и убывания.7. Промежутки знакопостоянства.8. Наибольшее и наименьшее значения.9. Ограниченность.10. Непрерывность.
Слайды и текст этой презентации
Слайд 1
Презентация по теме
«Тригонометрические функции»
(алгебра, 10 класс )
Учитель Пестова Е.В.
Функция
y = sin x
Слайд 2Основные свойства функции.
1. Область определения.
2. Область изменения.
3. Периодичность.
4. Четность, нечетность.
5.
Нули функции.
6. Промежутки возрастания и убывания.
7. Промежутки знакопостоянства.
8. Наибольшее и
наименьшее значения.9. Ограниченность.
10. Непрерывность.
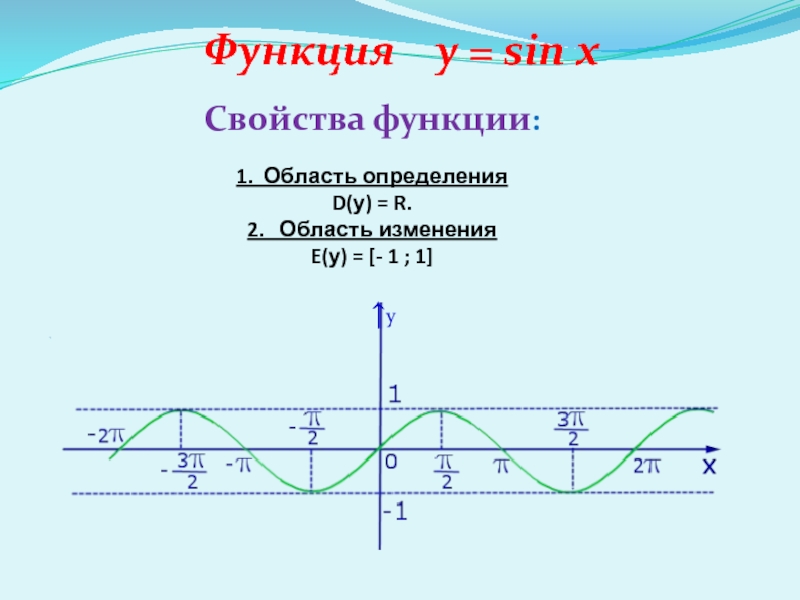
Слайд 3Функция y = sin x
Свойства функции:
1. Область определения
D(у)
= R.
2. Область изменения
E(у) = [- 1 ;
1]Слайд 4Функция y = sin x
Свойства функции:
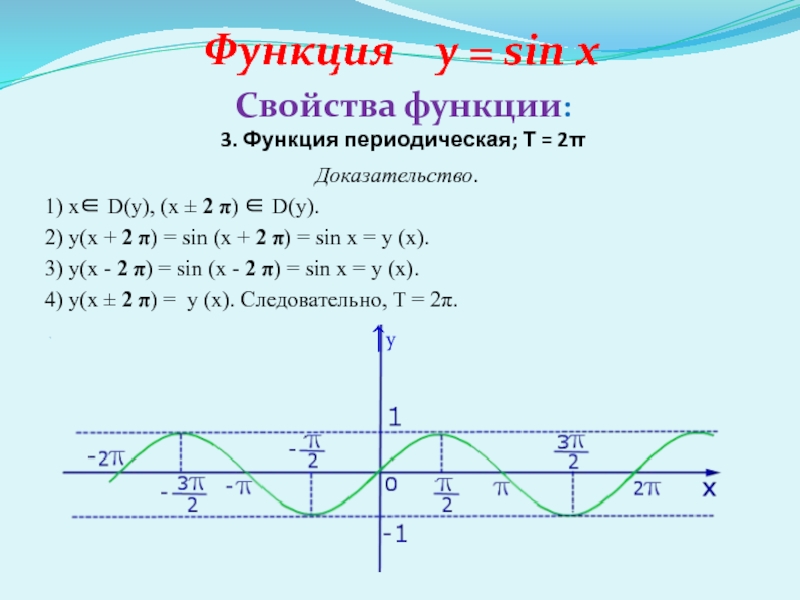
3. Функция периодическая;
Т = 2π
Доказательство.
1) x D(y), (x ± 2 π)
D(y). 2) y(x + 2 π) = sin (x + 2 π) = sin x = y (x).
3) y(x - 2 π) = sin (x - 2 π) = sin x = y (x).
4) y(x ± 2 π) = y (x). Следовательно, Т = 2π.
Слайд 5Функция y = sin x
Свойства функции:
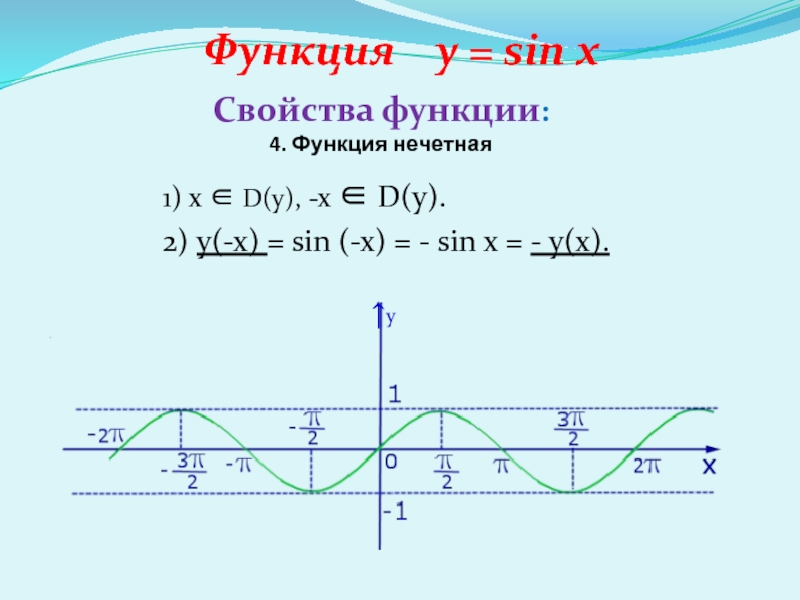
4. Функция нечетная
1) x
D(y), -x D(y).
2) y(-x) = sin (-x)
= - sin x = - y(x). Слайд 7Функция y = sin x
Свойства функции:
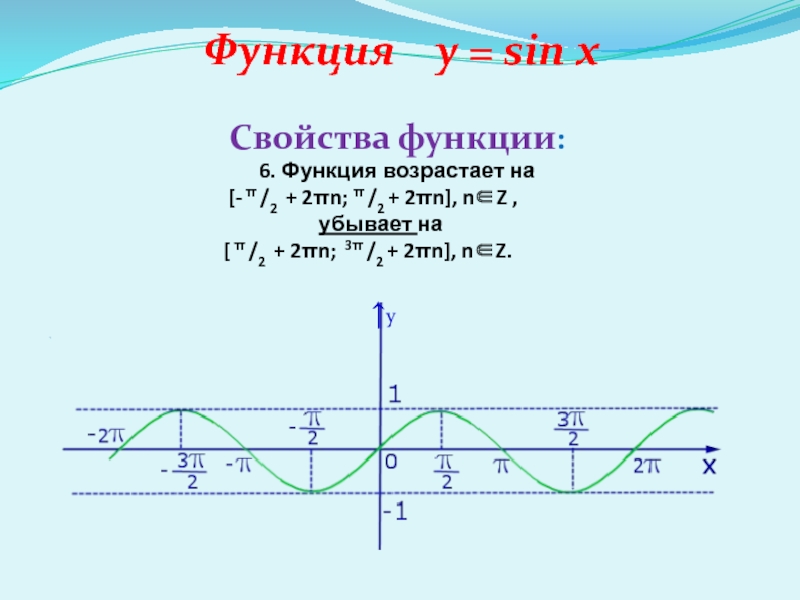
6. Функция возрастает на
[- π /2 + 2πn; π /2
+ 2πn], nZ ,убывает на
[ π /2 + 2πn; 3π /2 + 2πn], nZ.
Слайд 8
Доказательство.
1) При повороте точки вокруг начала координат против часовой
стрелки на угол от - π /2 до
π /2 ордината точки, т.е sin x, увеличивается от -1 до 1. Поэтому если - π /2 ≤ Х1 < Х2 ≤ π /2 , то sin Х1< sin Х2. Это означает, что функция y = sin x возрастает на [- π /2 ; π /2 ].2) Т.к. функция периодическая с периодом Т = 2π, то она возрастает на [- π /2 + 2πn; π /2 + 2πn], nZ .
3) Убывание функции на [ π /2 + 2πn; 3π /2 + 2πn], nZ, доказывается аналогично.
у
π /2
х
1
- π /2
-1
Слайд 9Функция y = sin x
Свойства функции:
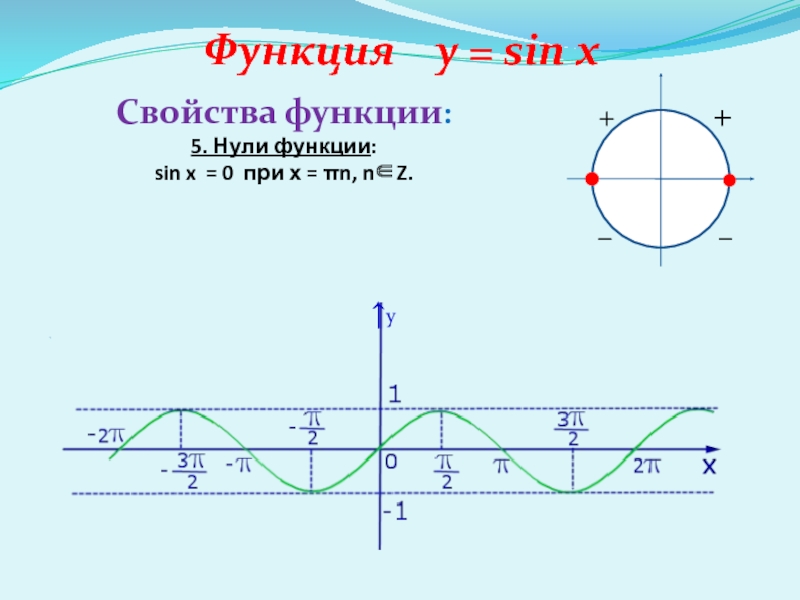
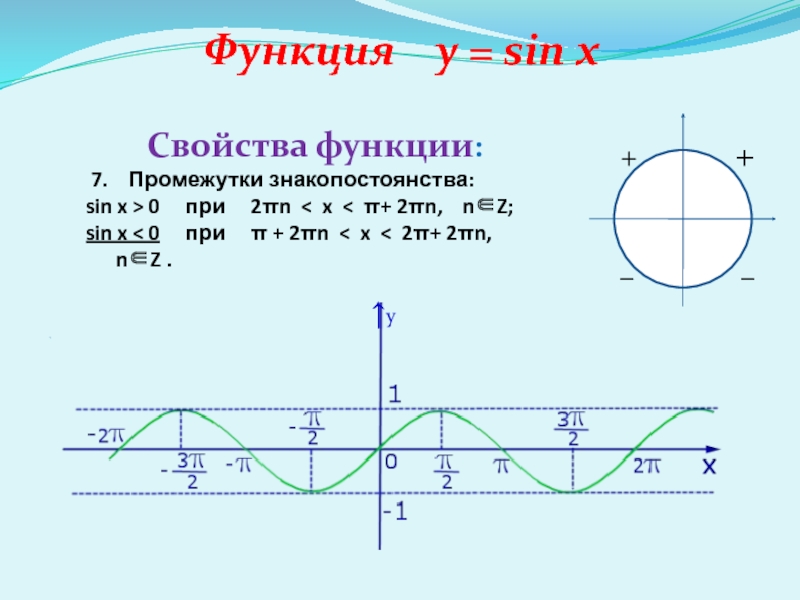
7. Промежутки
знакопостоянства:
sin x > 0 при 2πn
< x < π+ 2πn, nZ;sin x < 0 при π + 2πn < x < 2π+ 2πn, nZ .
+ +
_ _
Слайд 10Функция y = sin x
Свойства функции:
8. Наибольшее значение
функции у = 1;
наименьшее значение
функции у = -1.Ограничена сверху и снизу.
Непрерывна на всей области определения.



 " alt="Функция y = sin xСвойства функции: 7. Промежутки знакопостоянства:sin x > 0 при">
" alt="Функция y = sin xСвойства функции: 7. Промежутки знакопостоянства:sin x > 0 при">