Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Системы уравнений с двумя переменными
Содержание
- 1. Системы уравнений с двумя переменными
- 2. Решением системы уравнений с двумя переменными называется
- 3. Системы уравнений Графический способ Аналитический способ Метод подстановки
- 4. Метод подстановки Выразить из какого-нибудь уравнения системы
- 5. Умножьте почленно уравнения системы, подбирая множители так,
- 6. Построить график функции, заданной первым уравнением системы.Построить
- 7. Замени одно или два выражения в уравнениях
- 8. Слайд 8
- 9. x²-2y² =14, x²+2y²= 18; 2x² =32,
- 10. ух0На рисунке изображена парабола и три прямые. Укажите систему уравнений, которая не имеет решений.Задание 3Графический метод
- 11. Сколько решений имеет система уравнений?3-8yxУ = x2
- 12. ух011Такой системы нет43-4-4Пользуясь рисунком, укажите систему уравнений,Решением которой является пара Графический методЗадание 5
- 13. ух011Ответ:(;)111Используя графики функцийрешите уравнениеЗадание 6Графический методНАЙДИ ОШИБКУ!
- 14. 123Решить систему уравнений
- 15. Введение новой переменнойПример 1ЗаменаОтвет:(1;27), (27;1).
- 16. Решим систему уравнений Из второго уравнения системы
- 17. Решим систему уравнений Первое уравнение системы равносильно
- 18. Системы тригонометрических уравненийhttp://ege.sdamgia.ru/test?theme=203
- 19. 1.
- 20. 1.
- 21. 1.
- 22. 1.
- 23. 1.
- 24. 1.
- 25. Скачать презентанцию
Решением системы уравнений с двумя переменными называется пара значений переменных (x;y), обращающая каждое уравнение системы в верное равенство.Решить систему уравнений – значит найти все её решения или доказать, что решений нет.
Слайды и текст этой презентации
Слайд 1СИСТЕМЫ УРАВНЕНИЙ
С ДВУМЯ ПЕРЕМЕННЫМИ
Методы решения
МБОУ «Гимназия № 94» Московского
района г. Казани
Слайд 2Решением системы уравнений с двумя переменными называется пара значений переменных (x;y),
обращающая каждое уравнение системы в верное равенство.
Решить систему уравнений –
значит найти все её решения или доказать, что решений нет. 
Слайд 3Системы уравнений
Графический способ
Аналитический способ
Метод подстановки
Метод сложения
Метод
замены пере
менной
Слайд 4Метод подстановки
Выразить из какого-нибудь уравнения системы одну переменную через другую.
Подставить
в другое уравнение системы вместо этой переменной полученное выражение.
Решить получившееся
уравнение с одной переменной.Найти соответствующее значение второй переменной.
Слайд 5Умножьте почленно уравнения системы, подбирая множители так, чтобы коэффициенты при
одной из переменных стали противоположными числами.
Сложите почленно левые и правые
части уравнений системы.Решите получившееся уравнение с одной переменной.
Найдите соответствующее значение второй переменной.
Метод сложения
Слайд 6Построить график функции, заданной первым уравнением системы.
Построить график функции, заданной
вторым уравнением системы.
Определить координаты точек пересечения графиков функций.
Графический метод
Слайд 7Замени одно или два выражения в уравнениях системы новыми переменными
так, чтобы вновь полученные уравнения стали более простыми.
Реши полученную систему
уравнений методом, наиболее подходящим для этой системы уравнений.Сделай обратную замену, для того, чтобы найти значения первоначальных переменных.
Запиши ответ в виде пар значений (x,y), которые были найдены на третьем шаге.
Введение новой переменной
Слайд 8 Задание 1
a) x²=-y²-3xy-1,
б) x²+y²+3xy =-1, в) x²+y²+3xy =-1,
x+2y= 0; 2y=-x; x=-2y. x²+y²+3xy =-1,
x+2y= 0;
Какой из учеников применил метод подстановки
наиболее рационально?
Метод подстановки
Слайд 9 x²-2y² =14,
x²+2y²= 18;
2x² =32,
+
x²
=16,
x =4;
Можно ли записывать ответ?
Метод сложения
Задание 2
Слайд 10у
х
0
На рисунке изображена парабола и три прямые.
Укажите систему уравнений,
которая не имеет решений.
Задание 3
Графический метод
Слайд 11Сколько решений имеет система уравнений?
3
-8
y
x
У = x2 – 8
У =3х-3
Задание 4
Графический метод
НАЙДИ ОШИБКУ!
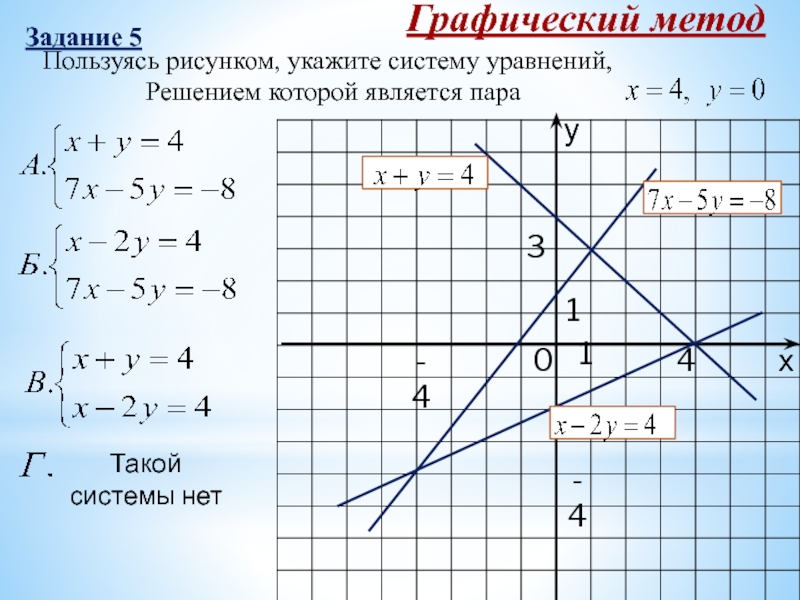
Слайд 12у
х
0
1
1
Такой системы нет
4
3
-4
-4
Пользуясь рисунком, укажите систему уравнений,
Решением которой является пара
Графический метод
Задание 5
Слайд 13у
х
0
1
1
Ответ:
(
;
)
1
1
1
Используя графики
функций
решите уравнение
Задание 6
Графический метод
НАЙДИ ОШИБКУ!
Слайд 16Решим систему уравнений
Из второго уравнения системы находим 2х-у=1, откуда
у=2х-1.
Подставляя вместо у в первое уравнение выражение 2х-1
получим
, откуда .Обозначим , получим квадратное уравнение
. Находим корни этого уравнения:
.
Уравнение замены решений не имеет. Корнем
уравнения является число х=2.
Соответствующее значение у=3.
Ответ:(2;3).
Системы показательных уравнений
Пример 2
Слайд 17Решим систему уравнений
Первое уравнение системы равносильно уравнению у-х=2, а
второе
– уравнению , причём
х>0 и у>0. Подставляяу=х+2 в уравнение , получим х(х+2)=48, откуда
,т.е. х= -8 или х=6.Но так как х>0, то х=6 и
тогда у=8. Итак, данная система уравнений имеет одно
решение: х=6, у=8.
Ответ: (6;8).
Системы логарифмических уравнений
Пример 3
