Применение метода проектов на уроках математики "Параллельная проекция и ее свойства"

преподаватель математики



Краевое государственное бюджетное образовательное учреждение среднего профессионального образования «Хабаровский

судостроительный колледж», Хабаровский край

Параллельная проекция и ее свойства

и ее свойства».
В данном уроке использованы следующие методы обучения:
лекция (на

этапе изучения нового материала),
работа в интерактивной среде – самостоятельное систематизация «открытых» знаний
лабораторная работа (во время открытия новых знаний, расширения и углубления знаний)

учащихся к самостоятельной исследовательской, поисковой деятельности, постановке перед ними целей

и проблем, решение которых ведёт к открытию и появлению новых знаний и умений, проект развивает пространственное представление и воображение.

параллельной проекции,
формирование первичных умений решать задачи, используя свойства параллельной проекции,
создание

условий для формирования аналитических способностей (умений сравнивать, сопоставлять, делать выводы и умозаключения).

Сайт «Начертательная геометрия»,
Учебник «Геометрия» 10-11 классы Л. С. Атанасян и др., учебник для общеобразовательных учреждений
ПК, мультимедийный проектор

мультимедийный класс

Оборудование урока:

Место проведения урока:

открытие свойств параллельной проекции (лабораторная работа №1)
Углубление и систематизация знаний

– свойства параллельной проекции
Первичное закрепление - использование интерактивной среды
Исследовательские задачи применение свойств параллельной проекции (лабораторная работа №2)
Изучение нового материала – ортогональная проекция (использование интерактивной среды)
Исследовательские задачи на изучение свойств ортогональной проекции (лабораторная работа №3)
Итог урока

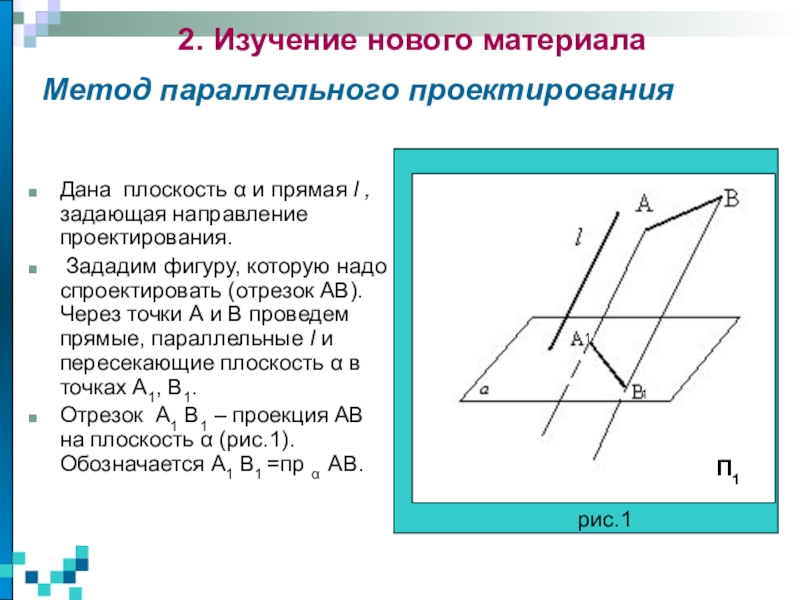
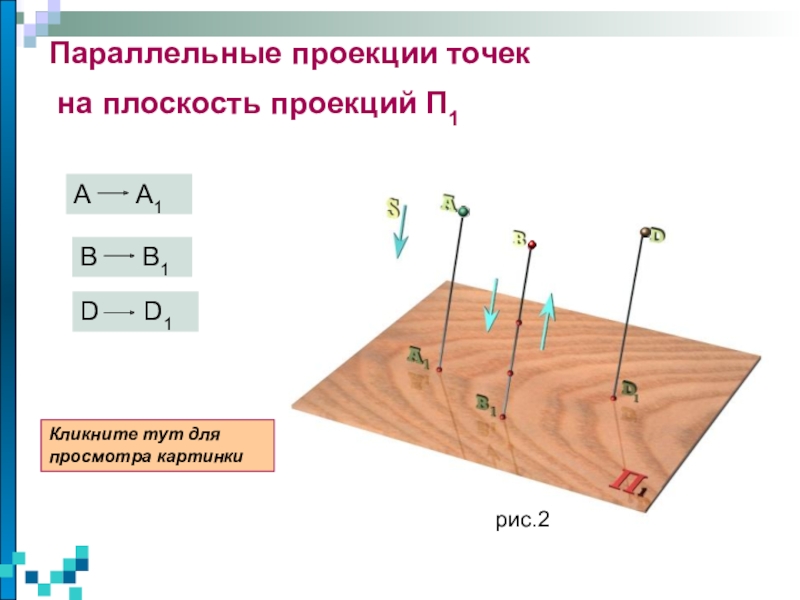
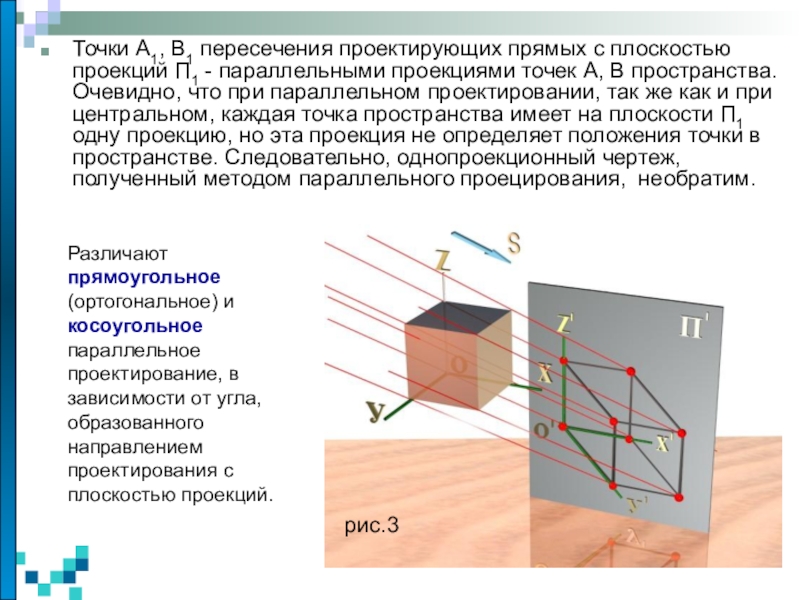
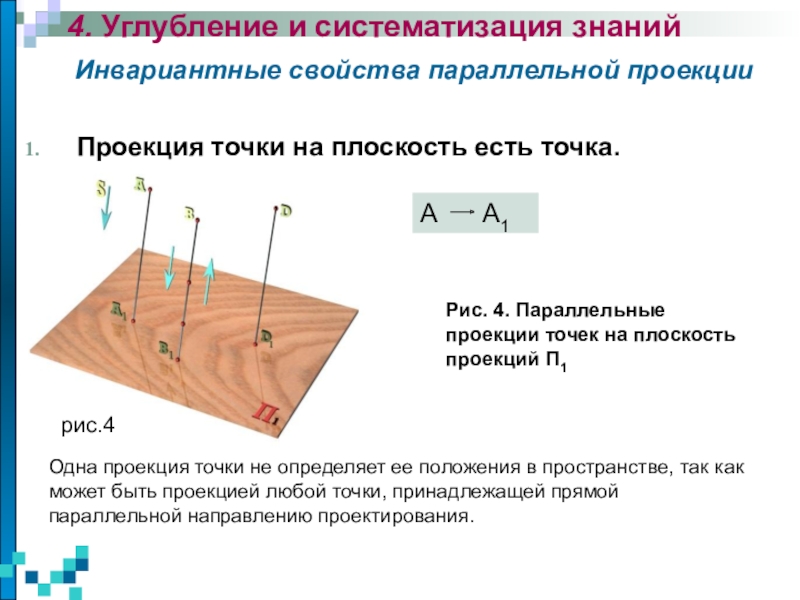
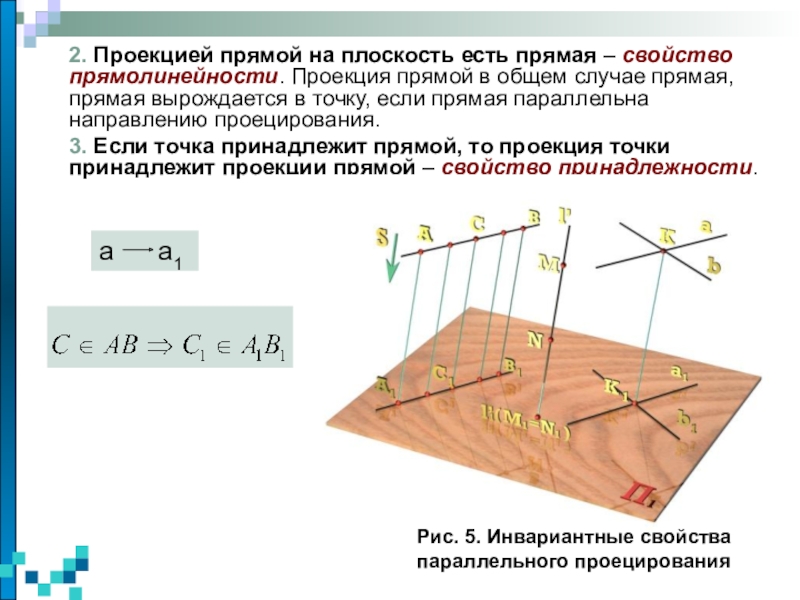
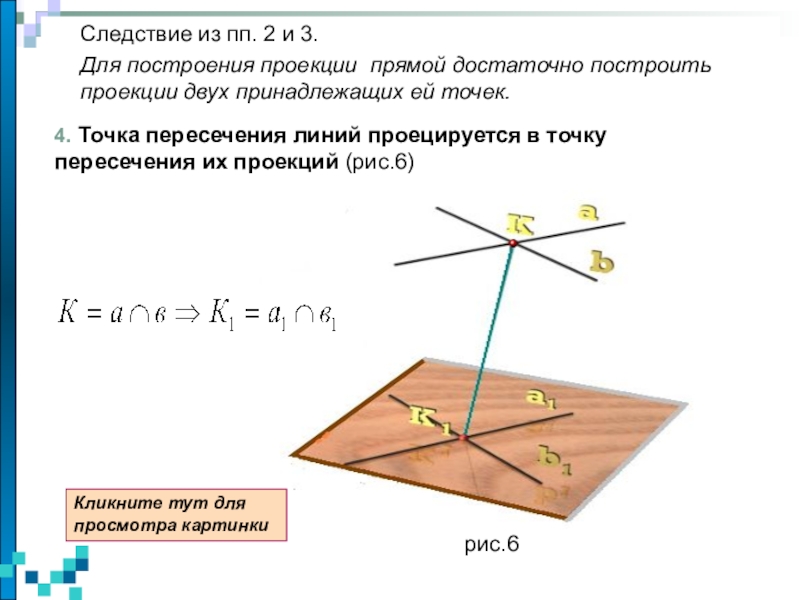
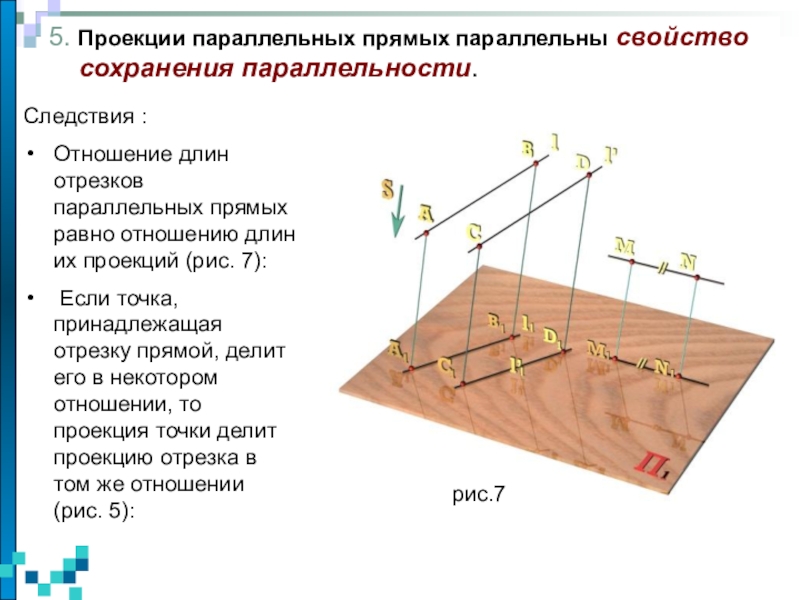
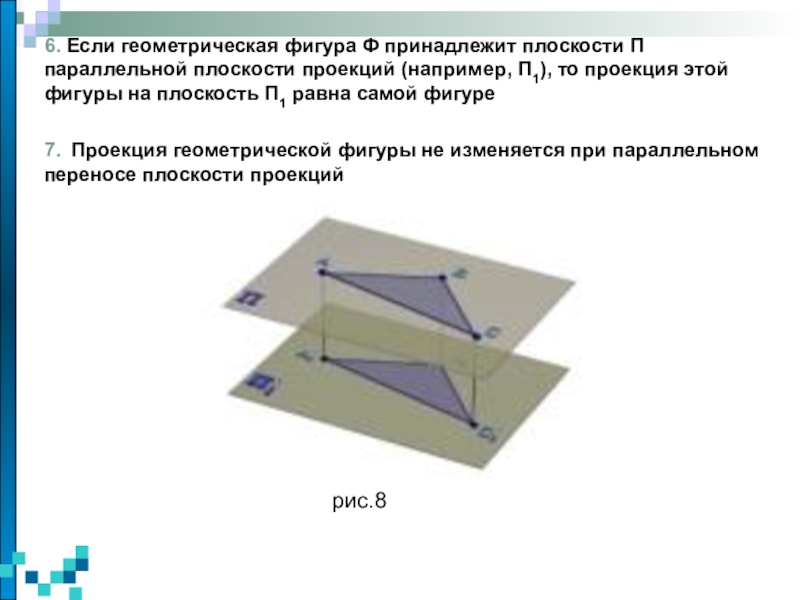
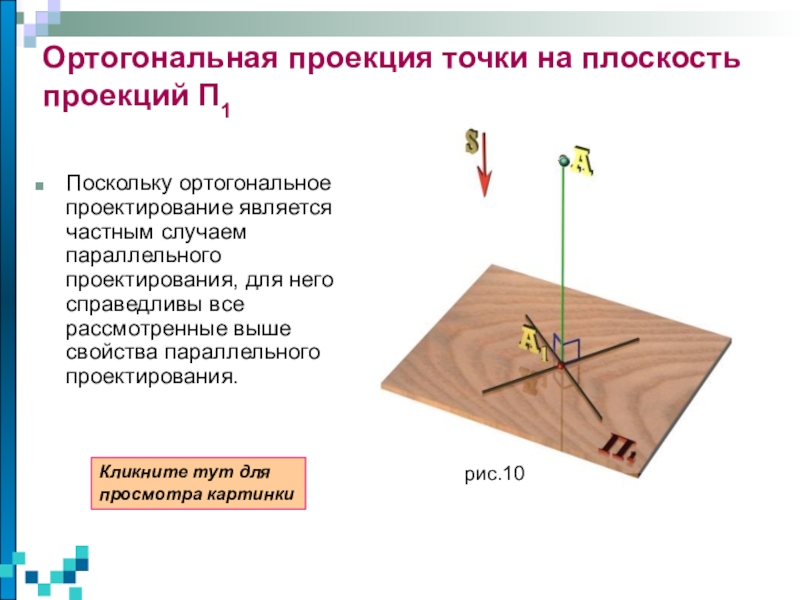
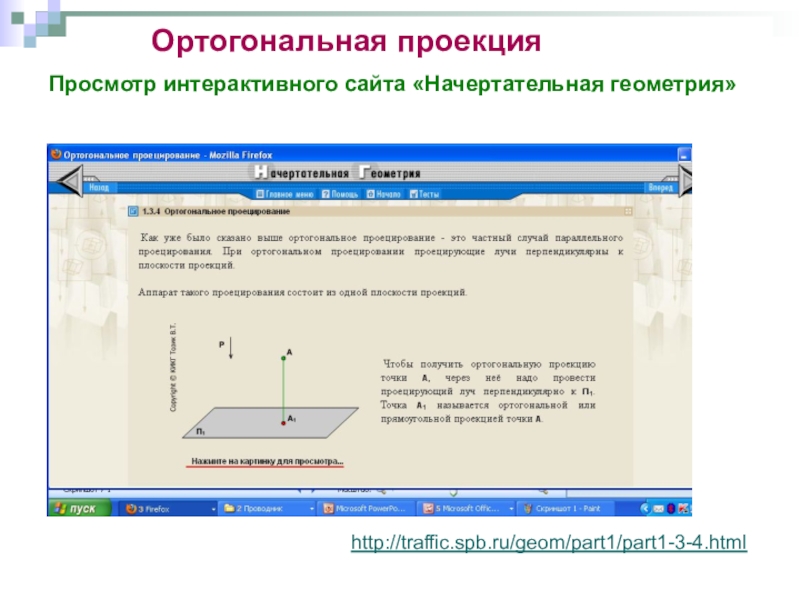
изучаются пространственные фигуры, однако на чертеже они изображаются в виде

плоских фигур. Каким же образом следует изображать пространственную фигуру на плоскости? Обычно в геометрии для этого используется параллельное проектирование пространственной фигуры на плоскость.
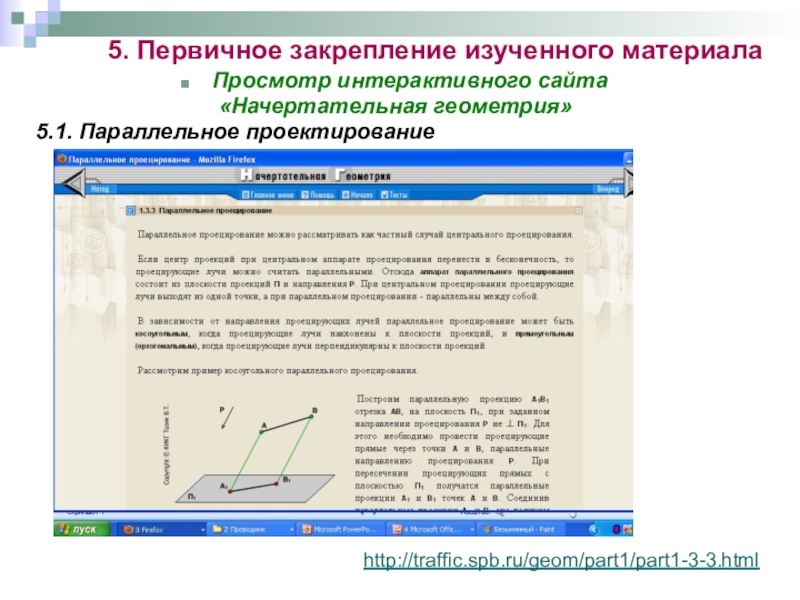
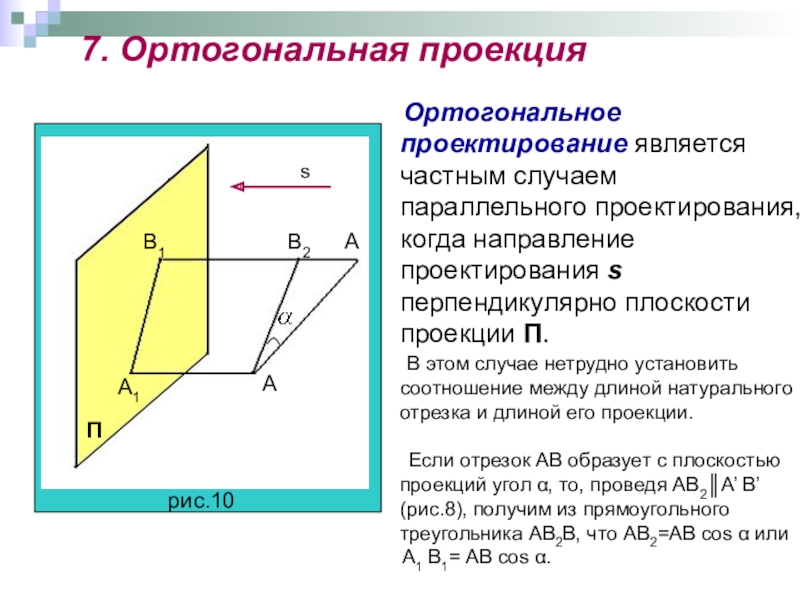
Сегодня первый урок по параллельному проектированию – рассмотрим параллельную проекцию и ее частные случаи прямоугольное (ортогональное) и косоугольное параллельное проектирование.
Умение изображать пространственные фигуры необходимо не только будущему математику, физику, инженеру, конструктору, но и скульптору, архитектору, художнику, дизайнеру и вообще каждому человеку. Обучаясь правильно изображать пространственные фигуры, вы знакомитесь с законами восприятия окружающих предметов, приобретаете необходимые практические навыки, формируете свои пространственные представления.
Решение пространственных задач по геометрии, как правило, требует выполнение чертежа, и от того, насколько правильно он выполнен, во многом зависит успешность решения самой задачи.

направление проектирования.
Зададим фигуру, которую надо спроектировать (отрезок AB). Через

точки А и В проведем прямые, параллельные l и пересекающие плоскость α в точках A1, B1.
Отрезок A1 B1 – проекция АВ на плоскость α (рис.1). Обозначается A1 B1 =пр α AB.

2. Изучение нового материала

1

1

П1

рис.1

просмотра картинки
рис.2
А А1
В В1
D

D1

- параллельными проекциями точек А, В пространства. Очевидно, что при

параллельном проектировании, так же как и при центральном, каждая точка пространства имеет на плоскости П1 одну проекцию, но эта проекция не определяет положения точки в пространстве. Следовательно, однопроекционный чертеж, полученный методом параллельного проецирования, необратим.

рис.3

Различают прямоугольное (ортогональное) и косоугольное параллельное проектирование, в зависимости от угла, образованного направлением проектирования с плоскостью проекций.

параллельных солнечных лучей.

Геометрические фигуры, в общем случае, проектируются на плоскость

проекции с искажением. В частности, при параллельном проецировании нарушаются метрические характеристики геометрических фигур (происходит искажение линейных и угловых величин). Но некоторые свойства оригинала сохраняются и на его проекции. Такие свойства называют инвариантными.

свойств параллельной проекции
Исследовательские задачи
Чем является проекция точки на плоскость при

параллельном проектировании?
Определяет ли одна проекция точки ее положения в пространстве?
Чем является проекция прямой на плоскость при параллельном проектировании?
В каком случае параллельной проекцией прямой будет точка?
Сколько проекций точек, принадлежащих прямой надо построить, чтобы построить проекцию саму прямую?

одна прямая?

Сохраняются ли при параллельном проектировании: а) длины отрезков;

б) величины углов?

Верно ли, что если длина отрезка равна длине его параллельной проекции, то отрезок параллелен плоскости проектирования?

свойства параллельной проекции

Проекция точки на плоскость есть точка.
Рис. 4.

Параллельные проекции точек на плоскость проекций П1

Одна проекция точки не определяет ее положения в пространстве, так как может быть проекцией любой точки, принадлежащей прямой параллельной направлению проектирования.

рис.4

А А1

Проекция прямой в общем случае прямая, прямая вырождается в точку,

если прямая параллельна направлению проецирования.
3. Если точка принадлежит прямой, то проекция точки принадлежит проекции прямой – свойство принадлежности.

Рис. 5. Инвариантные свойства параллельного проецирования

а а1

достаточно построить проекции двух принадлежащих ей точек.
4. Точка пересечения линий

проецируется в точку пересечения их проекций (рис.6)

рис.6

Кликните тут для просмотра картинки

длин отрезков параллельных прямых равно отношению длин их проекций (рис.

7):
Если точка, принадлежащая отрезку прямой, делит его в некотором отношении, то проекция точки делит проекцию отрезка в том же отношении (рис. 5):

рис.7

проекций (например, П1), то проекция этой фигуры на плоскость П1

равна самой фигуре

7. Проекция геометрической фигуры не изменяется при параллельном переносе плоскости проекций

рис.8

Параллельное проектирование

Подумайте, проанализируйте чертежи и докажите справедливость перечисленных инвариантов параллельного проектирования.

2. Подумайте, сохраняются ли рассмотренные свойства (инварианты) параллельного проектирования при изменении направлении проецирования.
3. Какой фигурой является проекция плоского многоугольника?

Ответ:

Плоский многоугольник в общем случае проектируется в многоугольник с тем же числом вершин. Из свойств параллельного проектирования следует, что параллельной проекцией многоугольника является или многоугольник с тем же числом сторон или отрезок. Причем, если в многоугольнике какие-нибудь две стороны параллельны, то их проекции также будут параллельны.

прямых?






5. Точки A’, B’ являются параллельными проекциями точек A,

B. AA’ = a, BB’ = b. Точка C делит отрезок AB в отношении m : n. Найдите расстояние между точкой C и ее проекцией C’.

Ответ:

Две пересекающиеся прямые; две параллельные прямые; прямая и точка, ей не принадлежащая.

Ответ:

может служить параллельной проекцией равностороннего треугольника.
Подсказка - рисунок
Подсказка –

доказательство

рис.9

(рис. 10). Построим на одной из его сторон. например, AC

равносторонний треугольник AB1C так, чтобы точка B1 не принадлежала плоскости π. Обозначим через l прямую, проходящую через точки B1 и B. Тогда ясно, что треугольник ABC является параллельной проекцией треугольника AB1C на плоскость π в направлении прямой l.

рис.10

Назад

когда направление проектирования s перпендикулярно плоскости проекции П.

В этом случае нетрудно установить соотношение между длиной натурального отрезка и длиной его проекции.

Если отрезок AB образует с плоскостью проекций угол α, то, проведя AB2║A’ B’ (рис.8), получим из прямоугольного треугольника AB2B, что AB2=AB cos α или
A1 B1= AB cos α.

s

А

А1

А

В1

В2

7. Ортогональная проекция

рис.10

П

является частным случаем параллельного проектирования, для него справедливы все рассмотренные

выше свойства параллельного проектирования.

рис.10

Кликните тут для просмотра картинки

геометрия»

проекция прямой на плоскость при ортогональном проектировании?
Чем является проекция

окружности на плоскость при ортогональном проектировании?

6. Лабораторная работа №3 применение свойств ортогональной проекции

Ответ:

Проекцией окружности на плоскость при ортогональном проектировании может быть окружность, эллипс, отрезок.

Итог урока. Домашнее задание
Три точки проектируются на плоскость. Сколько при

этом получится точек на плоскости проекций?

Какие свойства прямоугольника сохраняются при параллельном проектировании?

Какие свойства ромба сохраняются при параллельном проектировании?

Кликните тут 5 раз
для просмотра картинки

А

С

D

В

E

П

3 исследовательские задачи домой

«Геометрия», 10-11 классы, учебник для общеобразовательных учреждений, изд. М.: Просвещение,

2012
Б.Г. Зив «Геометрия», дидактические материалы, 10 класс, изд. М.: Просвещение, 2011
http://geometry2006.narod.ru/Art/Lecture8.htm
http://lecprim.ru/gm/Gm/komplex_1.html
http://traffic.spb.ru/geom/part1/part1-3-3.html
http://ru.wikipedia.org/wiki/%D0%9F%D1%80%D0%BE%D0%B5%D0%BA%D1%86%D0%B8%D1%8F_%28%D0%B3%D0%B5%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D1%8F%29