Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Прототипы заданий ОГЭ. Задание №14.
Содержание
- 1. Прототипы заданий ОГЭ. Задание №14.
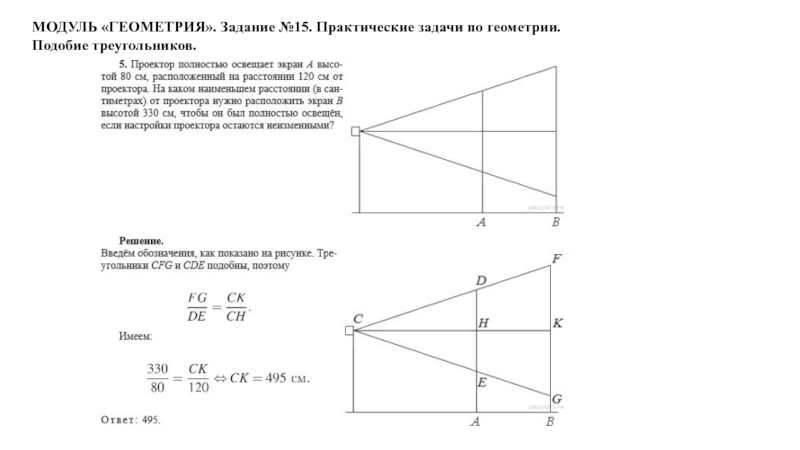
- 2. МОДУЛЬ «ГЕОМЕТРИЯ». Задание №15. Практические задачи по
- 3. МОДУЛЬ «ГЕОМЕТРИЯ». Задание №15. Практические задачи по
- 4. Задание №2. Сколько досок длиной 3,5 м,
- 5. Задание №2. Сколько досок длиной 3,5 м,
- 6. Задание №3.Определите, сколько необходимо закупить пленки для
- 7. Задание №3.Определите, сколько необходимо закупить пленки для
- 8. Задание № 4. На карте показан путь
- 9. Задание № 4. На карте показан путь
- 10. Задача № 5.Сколько досок длиной 4 м, шириной
- 11. Задача № 5.Сколько досок длиной 4 м, шириной
- 12. Задание №6.Наклонная крыша установлена на трёх вертикальных
- 13. Задание №6.Наклонная крыша установлена на трёх вертикальных
- 14. Задание № 7.Картинка имеет форму прямоугольника со
- 15. Задание № 7.Картинка имеет форму прямоугольника со
- 16. МОДУЛЬ «ГЕОМЕТРИЯ». Задание №15. Практические задачи по геометрии.Вычисление длин и площадей.
- 17. МОДУЛЬ «ГЕОМЕТРИЯ». Задание №15. Практические задачи по геометрии.Вычисление длин и площадей.
- 18. МОДУЛЬ «ГЕОМЕТРИЯ». Задание №15. Практические задачи по
- 19. МОДУЛЬ «ГЕОМЕТРИЯ». Задание №15. Практические задачи по
- 20. МОДУЛЬ «ГЕОМЕТРИЯ». Задание №15. Практические задачи по
- 21. МОДУЛЬ «ГЕОМЕТРИЯ». Задание №15. Практические задачи по
- 22. Задание №3.На каком расстоянии (в метрах) от
- 23. Задание №3.На каком расстоянии (в метрах) от
- 24. Задание № 4. Человек, рост которого равен
- 25. Задание № 4. Человек, рост которого равен
- 26. МОДУЛЬ «ГЕОМЕТРИЯ». Задание №15. Практические задачи по геометрии.Подобие треугольников.
- 27. МОДУЛЬ «ГЕОМЕТРИЯ». Задание №15. Практические задачи по геометрии.Подобие треугольников.
- 28. Задача №1. Два парохода вышли из порта,
- 29. Задача №1. Два парохода вышли из порта,
- 30. Задача №2. В 60 м одна от
- 31. Задача №2. В 60 м одна от
- 32. Задание №3. Сколько всего осей симметрии имеет
- 33. Задание №3. Сколько всего осей симметрии имеет
- 34. Задание №4. Определите высоту дома, ширина фасада
- 35. Задание №4. Определите высоту дома, ширина фасада
- 36. Задача № 5. Лестница соединяет точки
- 37. Задача № 5. Лестница соединяет точки
- 38. Задача №6. Обхват ствола секвойи равен 4,8
- 39. Задача №6. Обхват ствола секвойи равен 4,8
- 40. Задача №1.От столба высотой 9 м к
- 41. Задача №1.От столба высотой 9 м к
- 42. Задача № 2. Лестницу длиной 3 м
- 43. Задача № 2. Лестницу длиной 3 м
- 44. Задача № 3. Глубина крепостного рва равна
- 45. Задача № 3. Глубина крепостного рва равна
- 46. Задания № 4. Лестница соединяет точки A
- 47. Задания № 4. Лестница соединяет точки A
- 48. Задача № 5. Точка крепления троса, удерживающего
- 49. Задача №6. Длина стремянки в сложенном виде
- 50. Задача №6. Длина стремянки в сложенном виде
- 51. Задача № 7. Колесо имеет 18 спиц.
- 52. Задача № 7. Колесо имеет 18 спиц.
- 53. Задача № 8. На сколько градусов повернется
- 54. Задача № 8. На сколько градусов повернется
- 55. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1МОДУЛЬ «ГЕОМЕТРИЯ»
Задание №15. Практические задачи по геометрии.
Вычисление длин и площадей.
Подобие
треугольников.
Слайд 2МОДУЛЬ «ГЕОМЕТРИЯ». Задание №15. Практические задачи по геометрии.
Вычисление длин
и площадей.
Площадь прямоугольного земельного участка равна 9 га,
ширина участка
равна 150 м. Найдите длину этого участка в метрах.Слайд 3МОДУЛЬ «ГЕОМЕТРИЯ». Задание №15. Практические задачи по геометрии.
Вычисление длин
и площадей.
Задание №1.
Площадь прямоугольного земельного участка равна 9 га, ширина
участка равна 150 м. Найдите длину этого участка в метрах.Решение.
Переведем площадь участка в квадратные метры:
9 га = 90 000 м2.
Площадь прямоугольника равна произведению его смежных сторон. Поэтому, длина участка равна: 90 000 : 150 = 600 м.
Ответ: 600.
Слайд 4Задание №2.
Сколько досок длиной 3,5 м, шириной 20 см
и толщиной 20 мм выйдет из четырехугольной балки длиной 105
дм, имеющей в сечении прямоугольник размером 30 см 40 см?МОДУЛЬ «ГЕОМЕТРИЯ». Задание №15. Практические задачи по геометрии.
Вычисление длин и площадей.
Слайд 5Задание №2.
Сколько досок длиной 3,5 м, шириной 20 см
и толщиной 20 мм выйдет из четырехугольной балки длиной 105
дм, имеющей в сечении прямоугольник размером 30 см 40 см?Решение.
Найдем объем доски : 350 · 20 · 2 = 14 000 см3.
Найдем объем балки: 1050 · 30 · 40 = 1 260 000 см3.
Поэтому количество досок равно 1 260 000 : 14 000 = 90.
Ответ: 90.
МОДУЛЬ «ГЕОМЕТРИЯ». Задание №15. Практические задачи по геометрии.
Вычисление длин и площадей.
Слайд 6Задание №3.
Определите, сколько необходимо закупить пленки для гидроизоляции садовой дорожки,
изображенной на рисунке, если её ширина везде одинакова.
МОДУЛЬ «ГЕОМЕТРИЯ». Задание
№15. Практические задачи по геометрии.Вычисление длин и площадей.
Слайд 7Задание №3.
Определите, сколько необходимо закупить пленки для гидроизоляции садовой дорожки,
изображенной на рисунке, если её ширина везде одинакова.
МОДУЛЬ «ГЕОМЕТРИЯ». Задание
№15. Практические задачи по геометрии.Вычисление длин и площадей.
Решение: Разделим фигуру, изображенную на картинке на 3 прямоугольника. Найдем площадь первого прямоугольника: 5 · 1 = 5 м2. Найдем площадь второго прямоугольника: 4 · 1 = 4 м2. Найдем площадь третьего прямоугольника: 4 · 1 = 4 м2. Сложим все площади: 5 м2+4 м2 + 4 м2 = 13 м2.
Таким образом, потребуется закупить 13 м2 пленки.
Ответ: 13.
Слайд 8Задание № 4.
На карте показан путь Лены от дома
до школы. Лена измерила длину каждого участка и подписала его.
Используя рисунок, определите, длину пути (в м), если масштаб 1 см: 10000 см.МОДУЛЬ «ГЕОМЕТРИЯ». Задание №15. Практические задачи по геометрии.
Вычисление длин и площадей.
Слайд 9Задание № 4.
На карте показан путь Лены от дома
до школы. Лена измерила длину каждого участка и подписала его.
Используя рисунок, определите, длину пути (в м), если масштаб 1 см: 10000 см.МОДУЛЬ «ГЕОМЕТРИЯ». Задание №15. Практические задачи по геометрии.
Вычисление длин и площадей.
Решение:
Путь по карте равен 4 + 2 + 4 = 10 см. Так как масштаб равен 1 : 10000, Лена прошла 100 000 см или 1000 м.
Ответ: 1000.
Слайд 10Задача № 5.
Сколько досок длиной 4 м, шириной 20 см и толщиной
30 мм выйдет из бруса длиной 80 дм, имеющего в сечении прямоугольник
размером 30 см × 40 см?МОДУЛЬ «ГЕОМЕТРИЯ». Задание №15. Практические задачи по геометрии.
Вычисление длин и площадей.
Слайд 11Задача № 5.
Сколько досок длиной 4 м, шириной 20 см и толщиной
30 мм выйдет из бруса длиной 80 дм, имеющего в сечении прямоугольник
размером 30 см × 40 см?Решение:
Переведём все длины в метры.
Объём бруса равен 8 · 0,3 · 0,4 = 0,96 м3.
Объём одной доски 4 · 0,2 · 0,03 = 0,024 м3.
Получаем, что из бруса получится 0,96 : 0,024 = 40 досок.
Ответ: 40.
МОДУЛЬ «ГЕОМЕТРИЯ». Задание №15. Практические задачи по геометрии.
Вычисление длин и площадей.
Слайд 12Задание №6.
Наклонная крыша установлена на трёх вертикальных опорах, расположенных на
одной прямой. Средняя опора стоит посередине между малой и большой
опорами (см. рис.). Высота средней опоры 3,1 м, высота большей опоры 3,3 м. Найдите высоту малой опоры.МОДУЛЬ «ГЕОМЕТРИЯ». Задание №15. Практические задачи по геометрии.
Вычисление длин и площадей.
Слайд 13Задание №6.
Наклонная крыша установлена на трёх вертикальных опорах, расположенных на
одной прямой. Средняя опора стоит посередине между малой и большой
опорами (см. рис.). Высота средней опоры 3,1 м, высота большей опоры 3,3 м. Найдите высоту малой опорыМОДУЛЬ «ГЕОМЕТРИЯ». Задание №15. Практические задачи по геометрии.
Вычисление длин и площадей.
Решение.
Данная задача сводится к нахождению одного из оснований трапеции. Пусть длина неизвестного отрезка равна По теореме Фаллеса, получаем, что прямые, образованные опорами, отсекают на крыше равные отрезки. Поэтому средняя опора является средней линией трапеции. Средняя линия равна полусумме оснований трапеции: откуда получаем, что
Ответ: 2,9.
Слайд 14Задание № 7.
Картинка имеет форму прямоугольника со сторонами 19 см и 32 см. Её
наклеили на белую бумагу так, что вокруг картинки получилась белая
окантовка одинаковой ширины. Площадь, которую занимает картинка с окантовкой, равна 1080 см2. Какова ширина окантовки? Ответ дайте в сантиметрах.МОДУЛЬ «ГЕОМЕТРИЯ». Задание №15. Практические задачи по геометрии.
Вычисление длин и площадей.
Слайд 15Задание № 7.
Картинка имеет форму прямоугольника со сторонами 19 см и 32 см. Её
наклеили на белую бумагу так, что вокруг картинки получилась белая
окантовка одинаковой ширины. Площадь, которую занимает картинка с окантовкой, равна 1080 см2. Какова ширина окантовки? Ответ дайте в сантиметрах.МОДУЛЬ «ГЕОМЕТРИЯ». Задание №15. Практические задачи по геометрии.
Вычисление длин и площадей.
Решение:
Пусть см — ширина окантовки. Площадь прямоугольника равна произведению сторон., получаем уравнение:
Ответ: 4.
Слайд 16МОДУЛЬ «ГЕОМЕТРИЯ». Задание №15. Практические задачи по геометрии.
Вычисление длин и
площадей.
Слайд 17МОДУЛЬ «ГЕОМЕТРИЯ». Задание №15. Практические задачи по геометрии.
Вычисление длин и
площадей.
Слайд 18МОДУЛЬ «ГЕОМЕТРИЯ». Задание №15. Практические задачи по геометрии.
Подобие треугольников.
Задание №
1.
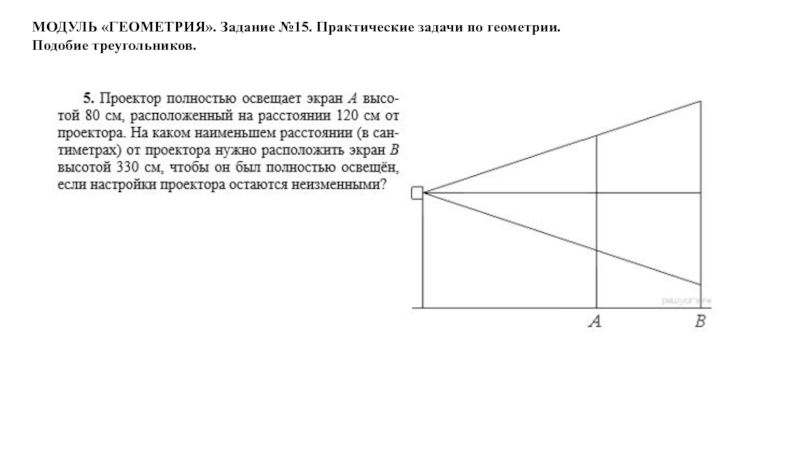
Проектор полностью освещает экран A высотой 80 см, расположенный
на расстоянии 250 см от проектора. На каком наименьшем расстоянии (в сантиметрах) от проектора нужно расположить экран B высотой 160 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными?Слайд 19МОДУЛЬ «ГЕОМЕТРИЯ». Задание №15. Практические задачи по геометрии.
Подобие треугольников.
Задание №
1.
Проектор полностью освещает экран A высотой 80 см, расположенный
на расстоянии 250 см от проектора. На каком наименьшем расстоянии (в сантиметрах) от проектора нужно расположить экран B высотой 160 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными?Решение. Заметим, что высота экрана, расположенного на расстоянии 250 см, в 2 раза меньше высоты экрана, расположенного на искомом расстоянии, значит, по теореме о средней линии, искомое расстояние в два раза больше первоначального экрана: 250·2 = 500.
Слайд 20МОДУЛЬ «ГЕОМЕТРИЯ». Задание №15. Практические задачи по геометрии.
Подобие треугольников.
Задания №2.
Человек
ростом 1,7 м стоит на расстоянии 8 шагов от столба,
на котором висит фонарь. Тень человека равна четырем шагам. На какой высоте (в метрах) расположен фонарь?Слайд 21МОДУЛЬ «ГЕОМЕТРИЯ». Задание №15. Практические задачи по геометрии.
Подобие треугольников.
Задания №2.
Человек
ростом 1,7 м стоит на расстоянии 8 шагов от столба,
на котором висит фонарь. Тень человека равна четырем шагам. На какой высоте (в метрах) расположен фонарь?Решение.
Столб и человек образуют два прямоугольных треугольниках ABC и FEB. Эти треугольники подобны по двум углам. Пусть высота фонаря равна , тогда
откуда
Поэтому фонарь расположен на высоте 5,1 м.
Ответ: 5,1.
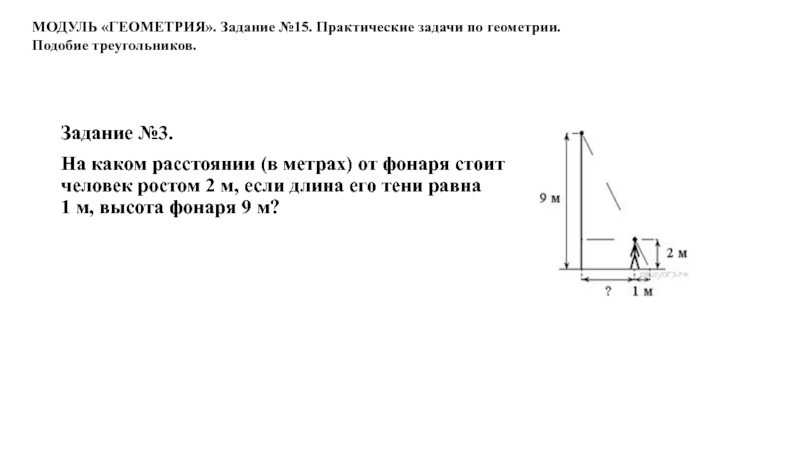
Слайд 22Задание №3.
На каком расстоянии (в метрах) от фонаря стоит человек
ростом 2 м, если длина его тени равна 1 м, высота фонаря 9
м?МОДУЛЬ «ГЕОМЕТРИЯ». Задание №15. Практические задачи по геометрии.
Подобие треугольников.
Слайд 23Задание №3.
На каком расстоянии (в метрах) от фонаря стоит человек
ростом 2 м, если длина его тени равна 1 м, высота фонаря 9
м?МОДУЛЬ «ГЕОМЕТРИЯ». Задание №15. Практические задачи по геометрии.
Подобие треугольников.
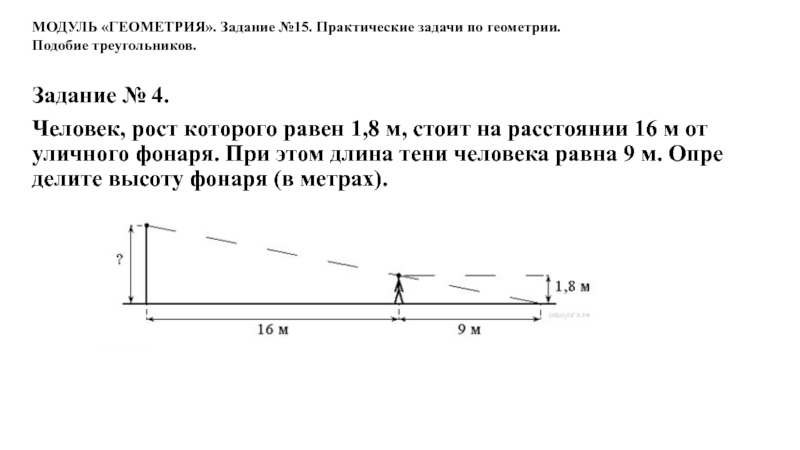
Слайд 24Задание № 4.
Человек, рост которого равен 1,8 м, стоит
на расстоянии 16 м от уличного фонаря. При этом длина
тени человека равна 9 м. Определите высоту фонаря (в метрах).МОДУЛЬ «ГЕОМЕТРИЯ». Задание №15. Практические задачи по геометрии.
Подобие треугольников.
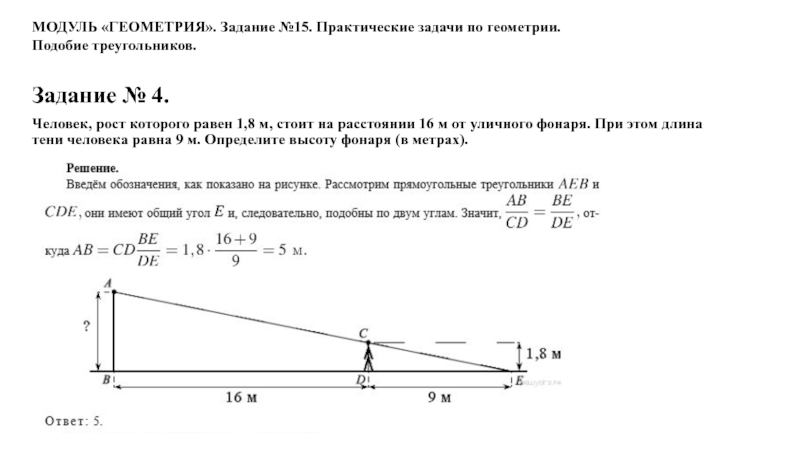
Слайд 25Задание № 4.
Человек, рост которого равен 1,8 м, стоит
на расстоянии 16 м от уличного фонаря. При этом длина
тени человека равна 9 м. Определите высоту фонаря (в метрах).МОДУЛЬ «ГЕОМЕТРИЯ». Задание №15. Практические задачи по геометрии.
Подобие треугольников.
Слайд 28Задача №1. Два парохода вышли из порта, следуя один на
север, другой на запад. Скорости их равны соответственно 15 км/ч
и 20 км/ч. Какое расстояние (в километрах) будет между ними через 2 часа?МОДУЛЬ «ГЕОМЕТРИЯ». Задание №15. Практические задачи по геометрии.
Разные задачи.
Слайд 29Задача №1. Два парохода вышли из порта, следуя один на
север, другой на запад. Скорости их равны соответственно 15 км/ч
и 20 км/ч. Какое расстояние (в километрах) будет между ними через 2 часа?Решение:
МОДУЛЬ «ГЕОМЕТРИЯ». Задание №15. Практические задачи по геометрии.
Разные задачи.
Слайд 30Задача №2.
В 60 м одна от другой растут две
сосны. Высота одной 31 м, а другой — 6 м.
Найдите расстояние (в метрах) между их верхушками.МОДУЛЬ «ГЕОМЕТРИЯ». Задание №15. Практические задачи по геометрии.
Разные задачи.
Слайд 31Задача №2.
В 60 м одна от другой растут две
сосны. Высота одной 31 м, а другой — 6 м.
Найдите расстояние (в метрах) между их верхушками.Решение:
МОДУЛЬ «ГЕОМЕТРИЯ». Задание №15. Практические задачи по геометрии.
Разные задачи.
Слайд 32Задание №3. Сколько всего осей симметрии имеет фигура, изображённая на
рисунке?
МОДУЛЬ «ГЕОМЕТРИЯ». Задание №15. Практические задачи по геометрии.
Разные задачи.
Слайд 33Задание №3. Сколько всего осей симметрии имеет фигура, изображённая на
рисунке?
МОДУЛЬ «ГЕОМЕТРИЯ». Задание №15. Практические задачи по геометрии.
Разные задачи.
Ось симметрии
данной фигуры — биссектрисса, проходящая через вершину звезды. Данная фигура имеет 5 осей симметрии.Ответ: 5.
Слайд 34Задание №4.
Определите высоту дома, ширина фасада которого равна
8 м, высота от фундамента до крыши равна 4 м,
а длина ската крыши равна 5 м.МОДУЛЬ «ГЕОМЕТРИЯ». Задание №15. Практические задачи по геометрии.
Разные задачи.
Слайд 35Задание №4.
Определите высоту дома, ширина фасада которого равна
8 м, высота от фундамента до крыши равна 4 м,
а длина ската крыши равна 5 м.МОДУЛЬ «ГЕОМЕТРИЯ». Задание №15. Практические задачи по геометрии.
Разные задачи.
Решение:
Крыша дома имеет форму равнобедренного треугольника. Высота этого треугольника является медианой и равна
Высота всего дома равна длине высоты крыши и высоты фундамента до крыши. Таким образом высота дома равна: 4 + 3 = 7 м.
Ответ: 7.
Слайд 36Задача № 5. Лестница соединяет точки и ,
расстояние между которыми равно 25 м. Высота каждой ступени равна
14 см, а длина — 48 см. Найдите высоту (в метрах), на которую поднимается лестница.МОДУЛЬ «ГЕОМЕТРИЯ». Задание №15. Практические задачи по геометрии.
Разные задачи.
Слайд 37Задача № 5. Лестница соединяет точки и ,
расстояние между которыми равно 25 м. Высота каждой ступени равна
14 см, а длина — 48 см. Найдите высоту (в метрах), на которую поднимается лестница.МОДУЛЬ «ГЕОМЕТРИЯ». Задание №15. Практические задачи по геометрии.
Разные задачи.
Решение:
Профиль каждой ступеньки имеет форму прямоугольного треугольника с катетами 14 и 48 см.
Найдём гипотенузу каждого из них:
Так как расстояние от A до B равно 25 метрам можем найти количество ступеней:
25 : 0,5 = 50 шт.
По условию задачи высота одной ступени равна 14 см, таким образом, найдем высоту
лестницы: 50 · 14 см = 700 см = 7 м.
Ответ: 7.
Слайд 38Задача №6.
Обхват ствола секвойи равен 4,8 м. Чему равен
его диаметр (в метрах)?
Ответ округлите до десятых.
МОДУЛЬ «ГЕОМЕТРИЯ». Задание
№15. Практические задачи по геометрии.Разные задачи.
Слайд 39Задача №6.
Обхват ствола секвойи равен 4,8 м. Чему равен
его диаметр (в метрах)?
Ответ округлите до десятых.
МОДУЛЬ «ГЕОМЕТРИЯ». Задание
№15. Практические задачи по геометрии.Разные задачи.
Поскольку длина окружности выражается через её диаметр формулой имеем
Ответ:1,5.
Слайд 40Задача №1.
От столба высотой 9 м к дому натянут провод,
который крепится на высоте 3 м от земли (см. рисунок).
Расстояние от дома до столба 8 м. Вычислите длину провода.МОДУЛЬ «ГЕОМЕТРИЯ». Задание №15. Практические задачи по геометрии.
Теорема Пифагора.
Слайд 41Задача №1.
От столба высотой 9 м к дому натянут провод,
который крепится на высоте 3 м от земли (см. рисунок).
Расстояние от дома до столба 8 м. Вычислите длину провода.МОДУЛЬ «ГЕОМЕТРИЯ». Задание №15. Практические задачи по геометрии.
Теорема Пифагора.
Слайд 42Задача № 2. Лестницу длиной 3 м прислонили к дереву.
На какой высоте (в метрах) находится верхний её конец, если
нижний конец отстоит от ствола дерева на 1,8 м?МОДУЛЬ «ГЕОМЕТРИЯ». Задание №15. Практические задачи по геометрии.
Теорема Пифагора.
Слайд 43Задача № 2. Лестницу длиной 3 м прислонили к дереву.
На какой высоте (в метрах) находится верхний её конец, если
нижний конец отстоит от ствола дерева на 1,8 м?МОДУЛЬ «ГЕОМЕТРИЯ». Задание №15. Практические задачи по геометрии.
Теорема Пифагора.
Слайд 44Задача № 3. Глубина крепостного рва равна 8 м, ширина
5 м, а высота крепостной стены от ее основания 20
м. Длина лестницы, по которой можно взобраться на стену, на 2 м больше, чем расстояние от края рва до верхней точки стены (см. рис.). Найдите длину лестницы.МОДУЛЬ «ГЕОМЕТРИЯ». Задание №15. Практические задачи по геометрии.
Теорема Пифагора.
Слайд 45Задача № 3. Глубина крепостного рва равна 8 м, ширина
5 м, а высота крепостной стены от ее основания 20
м. Длина лестницы, по которой можно взобраться на стену, на 2 м больше, чем расстояние от края рва до верхней точки стены (см. рис.). Найдите длину лестницы.МОДУЛЬ «ГЕОМЕТРИЯ». Задание №15. Практические задачи по геометрии.
Теорема Пифагора.
Решение:
Расстояние AB — гипотенуза прямоугольного треугольника с катетами 5 м и 20 − 8 = 12 м. Тем самым, длина AB равна 13 м, а длина лестницы равна 15 м.
Ответ: 15.
Слайд 46Задания № 4. Лестница соединяет точки A и B и
состоит из 35 ступеней. Высота каждой ступени равна 14 см,
а длина — 48 см. Найдите расстояние между точками A и B (в метрах).МОДУЛЬ «ГЕОМЕТРИЯ». Задание №15. Практические задачи по геометрии.
Теорема Пифагора.
Слайд 47Задания № 4. Лестница соединяет точки A и B и
состоит из 35 ступеней. Высота каждой ступени равна 14 см,
а длина — 48 см. Найдите расстояние между точками A и B (в метрах).МОДУЛЬ «ГЕОМЕТРИЯ». Задание №15. Практические задачи по геометрии.
Теорема Пифагора.
Слайд 48Задача № 5. Точка крепления троса, удерживающего флагшток в вертикальном
положении, находится на высоте 15 м от земли. Расстояние от
основания флагштока до места крепления троса на земле равно 8 м. Найдите длину троса.МОДУЛЬ «ГЕОМЕТРИЯ». Задание №15. Практические задачи по геометрии.
Теорема Пифагора.
Слайд 49Задача №6. Длина стремянки в сложенном виде равна 1,85 м,
а её высота в разложенном виде составляет 1,48 м. Найдите
расстояние (в метрах) между основаниями стремянки в разложенном виде.МОДУЛЬ «ГЕОМЕТРИЯ». Задание №15. Практические задачи по геометрии.
Теорема Пифагора.
Слайд 50Задача №6. Длина стремянки в сложенном виде равна 1,85 м,
а её высота в разложенном виде составляет 1,48 м. Найдите
расстояние (в метрах) между основаниями стремянки в разложенном виде.МОДУЛЬ «ГЕОМЕТРИЯ». Задание №15. Практические задачи по геометрии.
Теорема Пифагора.
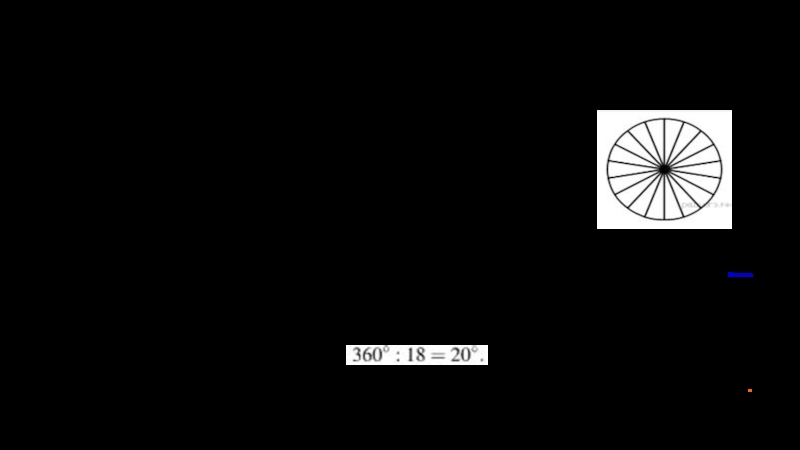
Слайд 51Задача № 7. Колесо имеет 18 спиц. Углы между соседними
спицами равны. Найдите угол, который образуют две соседние спицы. Ответ
дайте в градусах.МОДУЛЬ «ГЕОМЕТРИЯ». Задание №15. Практические задачи по геометрии.
Углы.
Слайд 52Задача № 7. Колесо имеет 18 спиц. Углы между соседними
спицами равны. Найдите угол, который образуют две соседние спицы. Ответ
дайте в градусах.МОДУЛЬ «ГЕОМЕТРИЯ». Задание №15. Практические задачи по геометрии.
Углы.
Решение.
Колесо представляет собой круг, 18 спиц которого делят на 18 круговых секторов. Так как развёрнутый угол равен 360° для каждого из секторов имеем:
Ответ: 20.
Слайд 53Задача № 8. На сколько градусов повернется Земля вокруг своей
оси за 7 часов?
МОДУЛЬ «ГЕОМЕТРИЯ». Задание №15. Практические задачи по
геометрии.Углы.
Слайд 54Задача № 8. На сколько градусов повернется Земля вокруг своей
оси за 7 часов?
Решение: За сутки Земля совершает полный оборот,
то есть поворачивается на 360°. Следовательно, за один час Земля поворачивается на 360° : 24 = 15°. Получаем, что за 7 часов Земля поворачивается на 7 · 15° = 105°.Ответ: 105.
МОДУЛЬ «ГЕОМЕТРИЯ». Задание №15. Практические задачи по геометрии.
Углы.