Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Расположение прямых и плоскостей в пространстве
Содержание
- 1. Расположение прямых и плоскостей в пространстве
- 2. ПЛАНИМЕТРИЯСТЕРЕОМЕТРИЯГЕОМЕТРИЯ на плоскостиГЕОМЕТРИЯ в пространстве«планиметрия» – наименование смешанного
- 3. точка,прямая,плоскость,расстояниеОсновные понятия стереометрии α = (РКС)|PK|A∉α ,
- 4. ВСПОМНИМ ПЛАНИМЕТРИЮКаково может быть взаимное расположение двух прямых на плоскости?Какие прямые в планиметрии называются параллельными?
- 5. ВСПОМНИМ ПЛАНИМЕТРИЮАксиома параллельных прямых - ?Через точку,
- 6. ВСПОМНИМ ПЛАНИМЕТРИЮСледствия аксиомы параллельных прямых - ?Если
- 7. Аксиомы стереометрииА-1Через любые три точки, не лежащие
- 8. Аксиомы стереометрииА-2Если две точки прямой лежат в
- 9. Аксиомы стереометрииА-3Если две плоскости имеют общую точку,
- 10. СЛЕДСТВИЯ ИЗ АКСИОМТ-1Через любую прямую и не
- 11. СЛЕДСТВИЕ ИЗ Т-1Через две ПАРАЛЛЕЛЬНЫЕ прямые можно провести плоскость, и притом только одну. к
- 12. СЛЕДСТВИЯ ИЗ АКСИОМТ-2Через любые две пересекающиеся прямые
- 13. По трем точкам, не лежащим на одной
- 14. ВЕРНЕМСЯ В ПРОСТРАНСТВО.Каково может быть взаимное расположение
- 15. ВЕРНЕМСЯ В ПРОСТРАНСТВОКакие прямые в пространстве называются
- 16. Теорема о параллельных прямых.Через любую точку пространства,
- 17. …они лежат на параллельных прямыхОтрезки в пространстве
- 18. Лемма о параллельных прямыхЕсли одна из параллельных
- 19. Лемма о параллельных прямыхДано: Доказать: b и имеют общую точку, причем она единственнаяab
- 20. abсРМДано: Доказать: b и имеют общую точку, причем она единственнаяЛемма о параллельных прямых
- 21. Теорема о параллельности трех прямых в пространстве.Если две прямые параллельны третьей прямой, то они параллельныabсДано:Доказать:и
- 22. Теорема о параллельности трех прямых в пространстве.Если
- 23. Задача №17.Дано: М – середина BD ABDCNMРQN
- 24. Взаимное расположение прямой и плоскости. Признак параллельности прямой и плоскости.
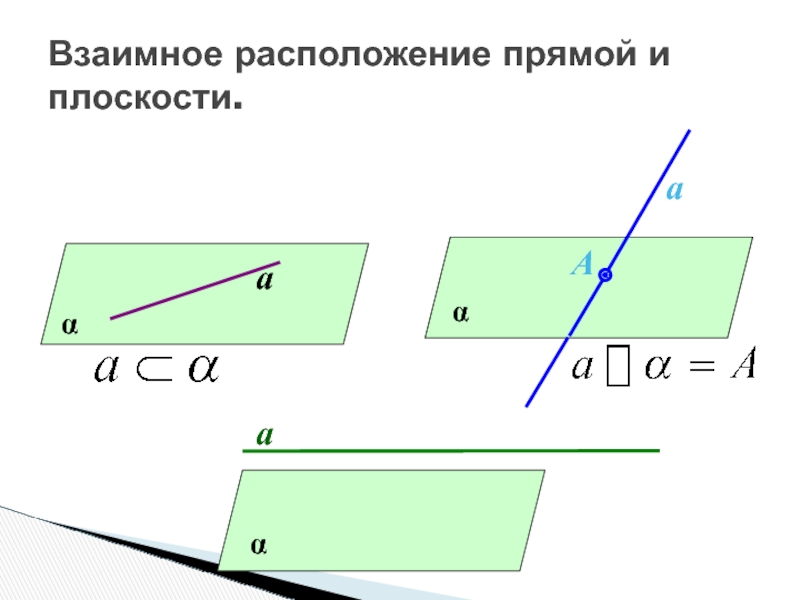
- 25. Взаимное расположение прямой и плоскости.αаαаАαа
- 26. Построение прямой, не пересекающей плоскость.α1. Проведем плоскость
- 27. Построение прямой, не пересекающей плоскость.αа1АβаДоказательство:1) Пусть а
- 28. Определение параллельности прямой и плоскости.Прямая и плоскость
- 29. Взаимное расположение прямой и плоскости.αаαаАαаа || α
- 30. Построение параллельных прямой и плоскости.а1аαа || а1а
- 31. На модели куба укажите плоскости, параллельные прямой
- 32. На модели куба укажите плоскости, параллельные прямой
- 33. Если плоскость проходит через данную прямую, параллельную
- 34. Если одна из двух параллельных прямых параллельна
- 35. Задача №18 (б)С1В1СВАαДоказать, что точки А, В1,
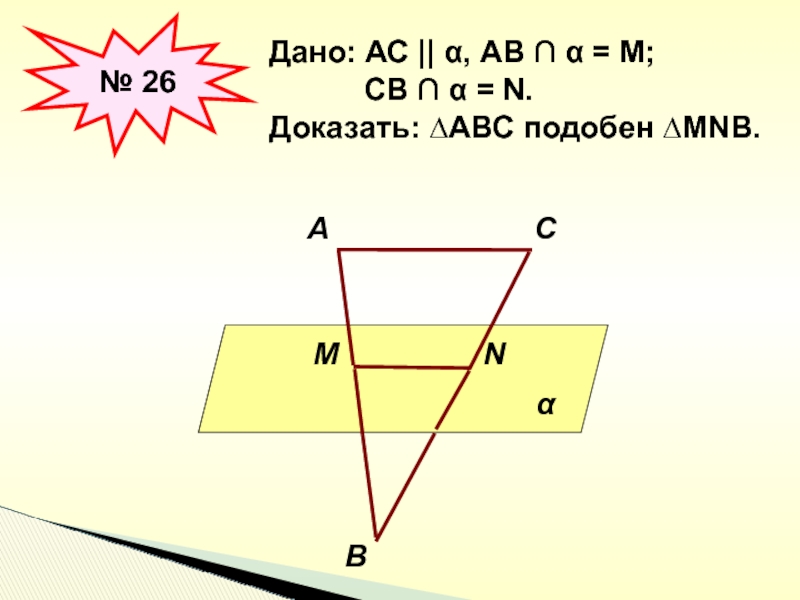
- 36. № 26Дано: АС || α, АВ ∩
- 37. Отрезок АВ не пересекает плоскость α. Через
- 38. Точка М лежит на отрезке АВ. Отрезок
- 39. Дан треугольник МКР. Плоскость, параллельная прямой МК,
- 40. Дано: АВСD – трапеция, ВС = 12
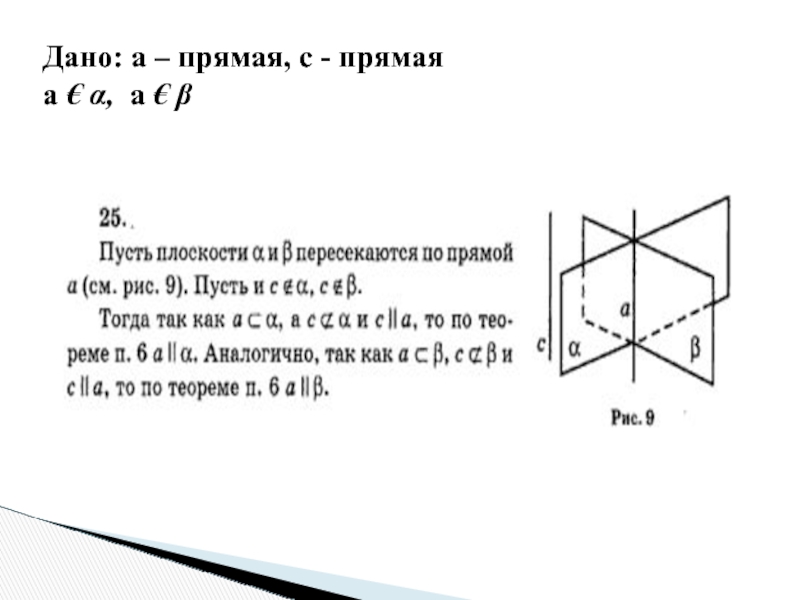
- 41. Дано: а – прямая, c - прямая а € α, а € β
- 42. Слайд 42
- 43. Слайд 43
- 44. Слайд 44
- 45. Слайд 45
- 46. Взаимное расположение прямых в пространстве.Угол между прямыми.
- 47. Любая прямая а, лежащая в плоскости, разделяет
- 48. Углы с сонаправленными сторонами.ОАО1А1Лучи ОА и О1А1
- 49. Теорема об углах с сонаправленными
- 50. Теорема об углах с сонаправленными
- 51. Теорема об углах с сонаправленными
- 52. Угол между скрещивающимися прямыми.α1800 - α00 <
- 53. Практическое задание.Выбрать любую точку М2.Построить А2В2|| АВ
- 54. Дан куб АВСDА1В1С1D1.Найдите угол между прямыми:1.ВС и СС12.900АС и ВС4503.D1С1 и ВС9004.А1В1 и АС450
- 55. ЗадачаДано: ОВ || СD,
- 56. Дополнительная задача.Треугольники АВС и АСD лежатв разных
- 57. Взаимное расположение прямых в пространстве.Скрещивающиеся прямые.
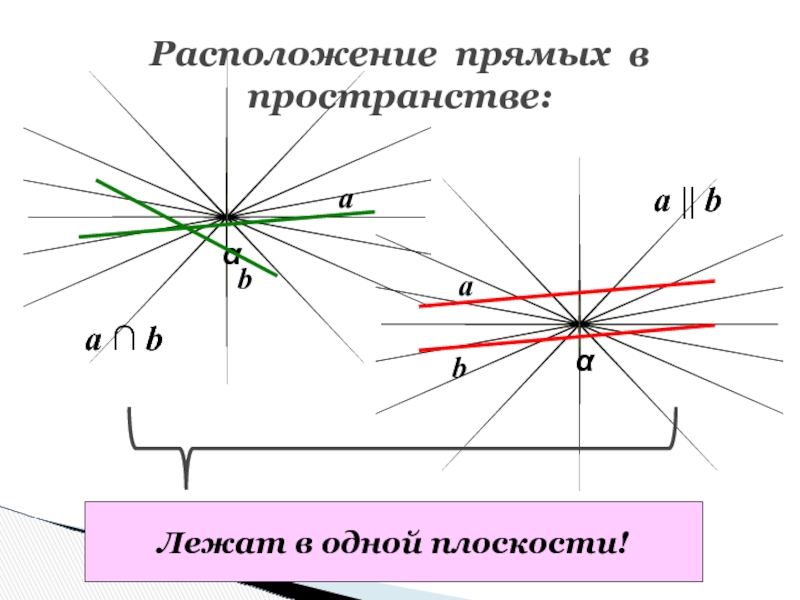
- 58. Расположение прямых в пространстве:ααababa ∩ ba || bЛежат в одной плоскости!
- 59. ???Дан куб АВСDA1B1C1D1Являются ли параллельными прямые
- 60. Признак скрещивающихся прямых.Если одна из двух прямых
- 61. Признак скрещивающихся прямых.Дано: АВ α,
- 62. Закрепление изученной теоремы:Определить взаимное расположение
- 63. Теорема:Через каждую из двух скрещивающихся прямых проходит
- 64. Задача.Построить плоскость α, проходящую через точку К
- 65. ЗадачаАВСDMNPР1КДано: D (АВС),АМ = МD;
- 66. ЗадачаАВСDMNPКДано: D (АВС),АМ = МD;
- 67. ЗадачаαabМNДано: a || bMN ∩ a = MОпределитьвзаимное расположениепрямых MN u b.Скрещивающиеся.
- 68. Взаимное расположение плоскостейПлоскости имеют одну общую точкуПлоскости
- 69. Свойства параллельных плоскостей
- 70. Теорема Если плоскость пересекает одну из
- 71. Доказательство Проведём в плоскости γ прямую а,
- 72. Теорема:Две плоскости, параллельные третьей, параллельны.
- 73. Доказательство:Пусть α∩ γ = с. сαβγПусть М∈
- 74. Если две пересекающиеся прямые одной плоскостисоответственно параллельны
- 75. Доказательство 1)По условию известно, что
- 76. МногогранникиТетраэдр
- 77. МногогранникиПараллелепипед
- 78. Свойства тетраэдраПравильный ТетраэдрТетра́эдр — многогранник с четырьмя
- 79. ПараллелепипедСвойстваПараллелепипед симметричен относительно середины его диагонали, соединяющей
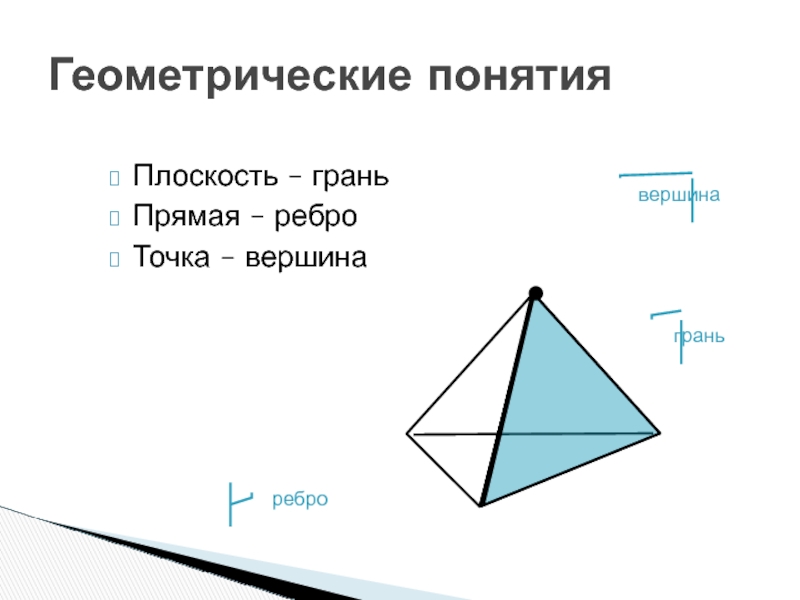
- 80. Геометрические понятияПлоскость – граньПрямая – реброТочка – вершинаграньребровершина
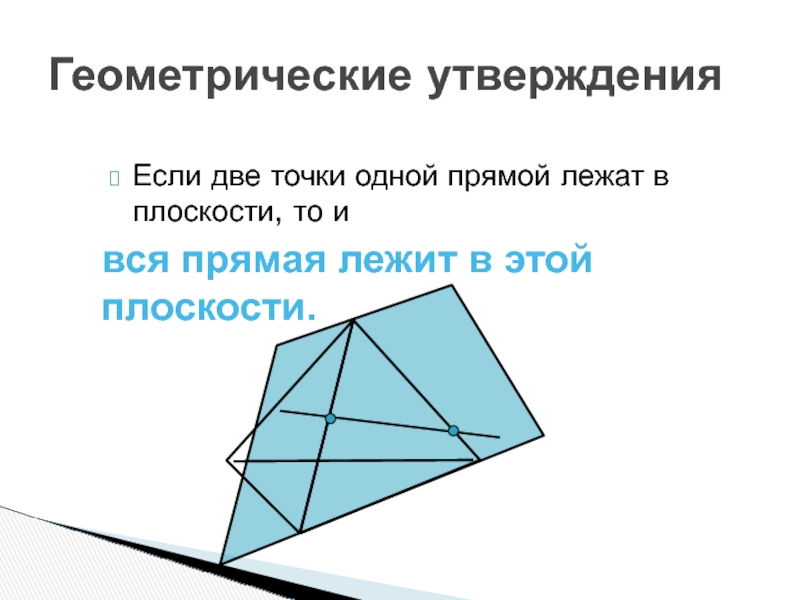
- 81. Геометрические утвержденияЕсли две точки одной прямой лежат в плоскости, то ився прямая лежит в этой плоскости.
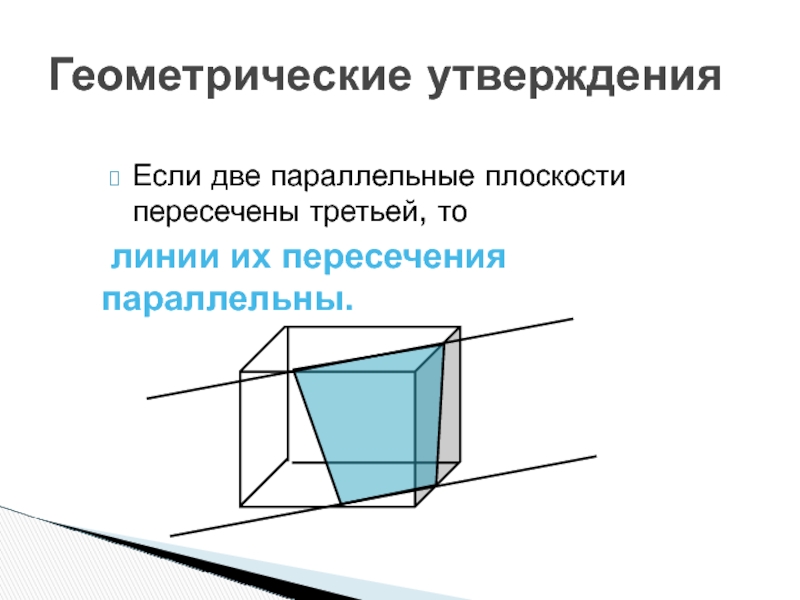
- 82. Геометрические утвержденияЕсли две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.
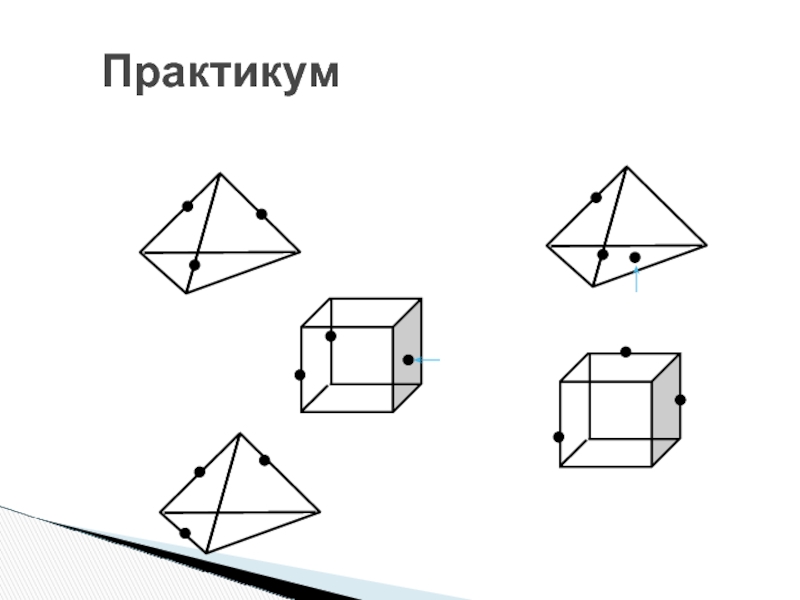
- 83. Практикум
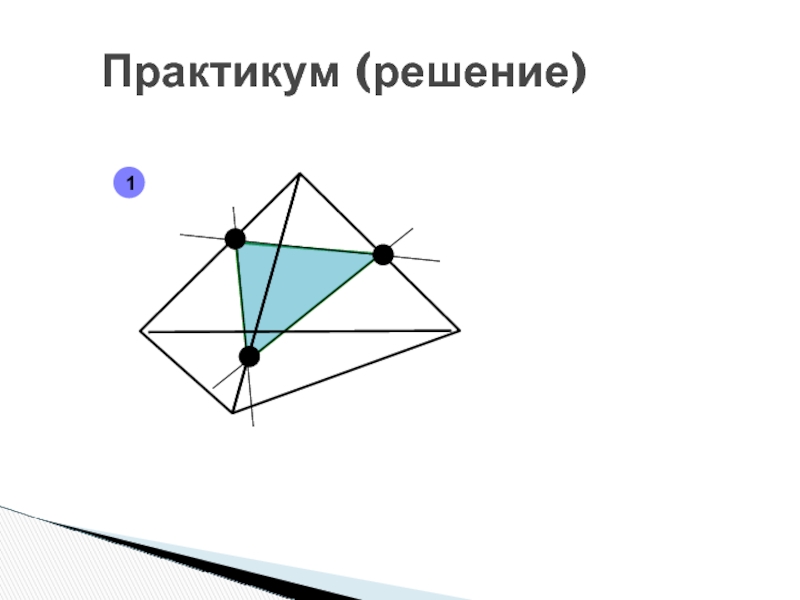
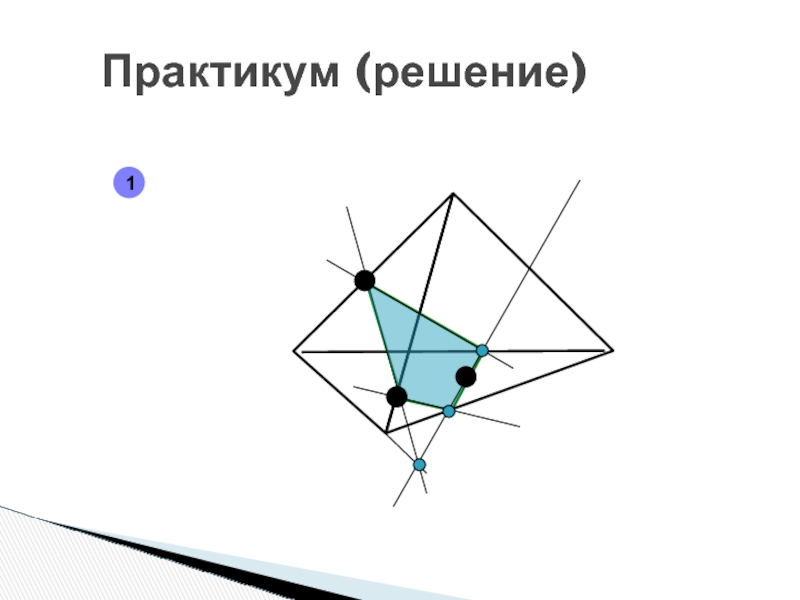
- 84. Практикум (решение)1
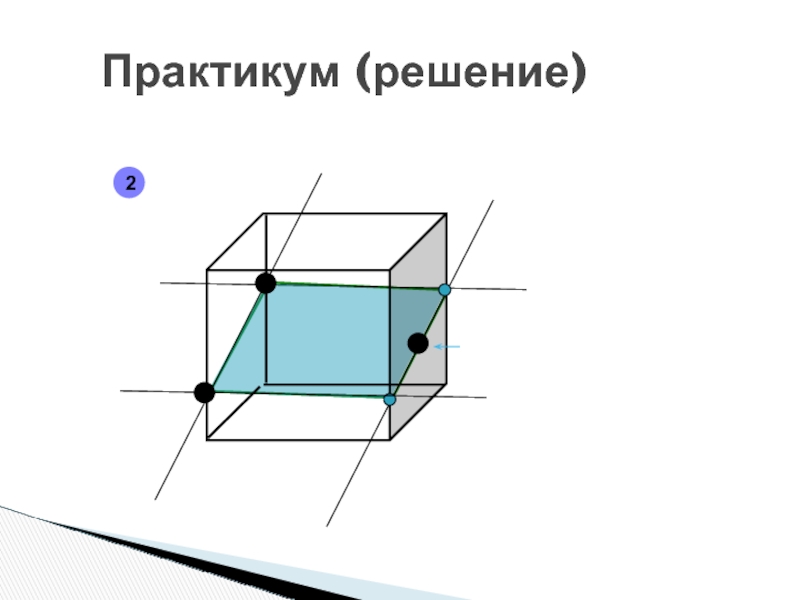
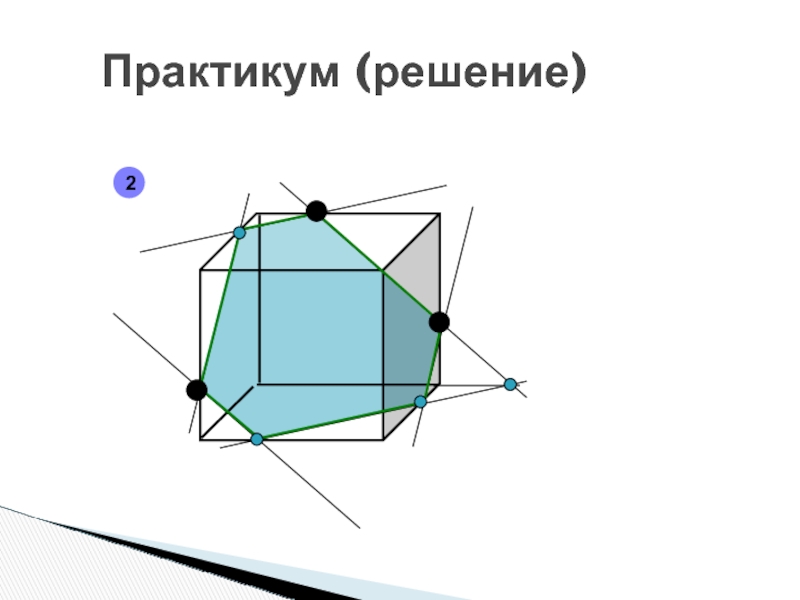
- 85. Практикум (решение)2
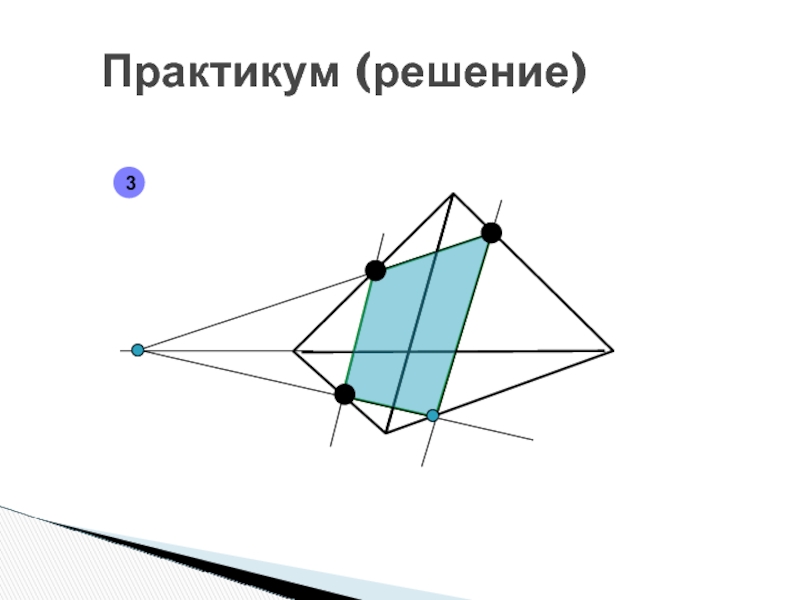
- 86. Практикум (решение)3
- 87. Практикум (решение)1
- 88. Практикум (решение)2
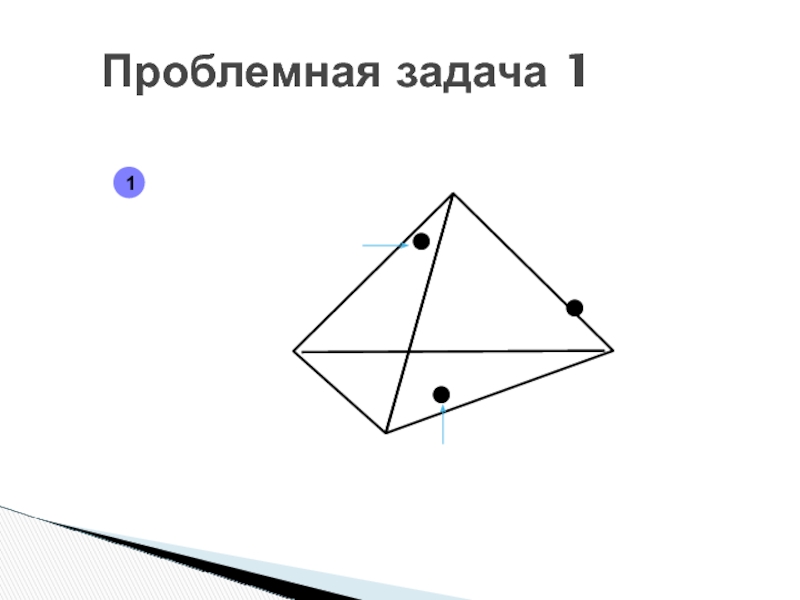
- 89. Проблемная задача 11
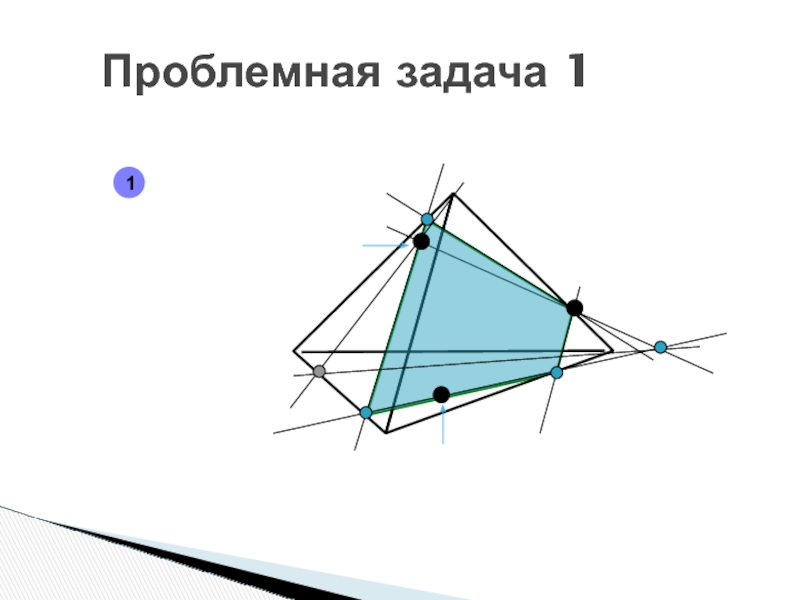
- 90. Проблемная задача 11
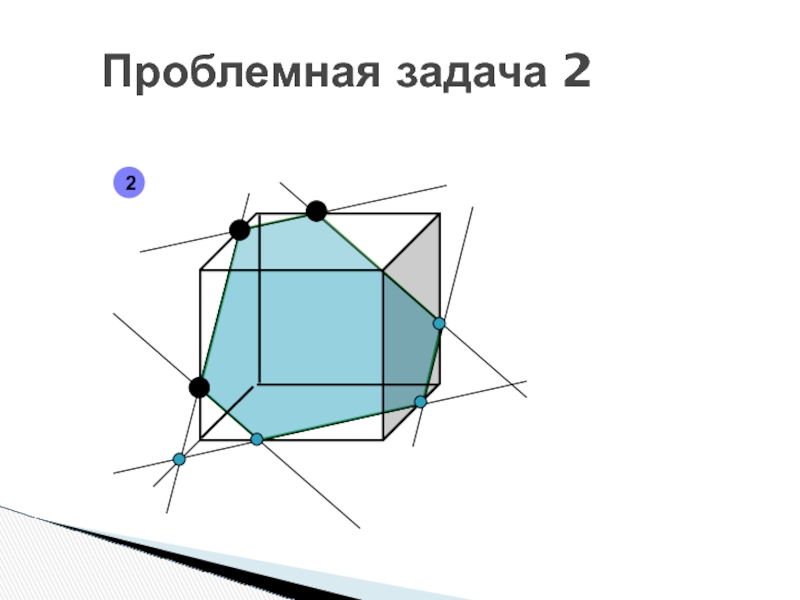
- 91. Проблемная задача 22
- 92. Проблемная задача 22
- 93. Спасибо за внимание!
- 94. Скачать презентанцию
ПЛАНИМЕТРИЯСТЕРЕОМЕТРИЯГЕОМЕТРИЯ на плоскостиГЕОМЕТРИЯ в пространстве«планиметрия» – наименование смешанного происхождения: от греч. metreo – измерять и лат. planum – плоская поверхность (плоскость)«стереометрия» – от греч. stereos – пространственный (stereon – объем). ГЕОМЕТРИИ
Слайды и текст этой презентации
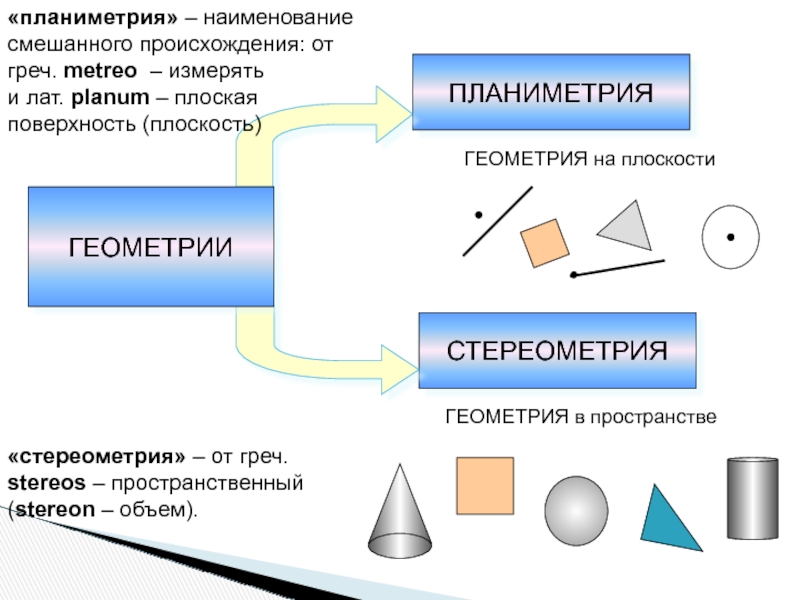
Слайд 2ПЛАНИМЕТРИЯ
СТЕРЕОМЕТРИЯ
ГЕОМЕТРИЯ на плоскости
ГЕОМЕТРИЯ в пространстве
«планиметрия» – наименование смешанного происхождения: от греч.
metreo – измерять
и лат. planum – плоская поверхность (плоскость)
«стереометрия» – от
греч. stereos – пространственный (stereon – объем). ГЕОМЕТРИИ
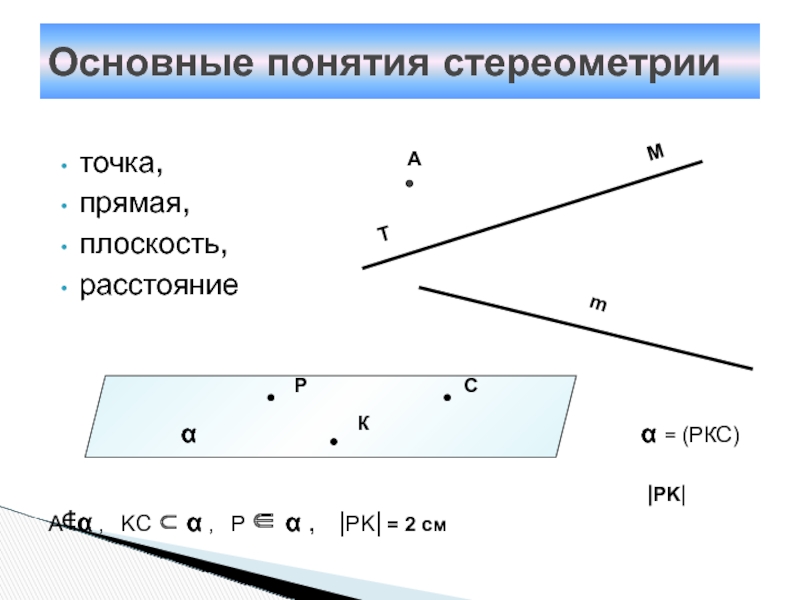
Слайд 3точка,
прямая,
плоскость,
расстояние
Основные понятия стереометрии
α = (РКС)
|PK|
A∉α , KC ⊂
α , P ∈ α , |PK| =
2 см
Слайд 4ВСПОМНИМ ПЛАНИМЕТРИЮ
Каково может быть взаимное расположение двух прямых на плоскости?
Какие
прямые в планиметрии называются параллельными?
Слайд 5
ВСПОМНИМ ПЛАНИМЕТРИЮ
Аксиома параллельных прямых - ?
Через точку, не лежащую на
данной прямой,
проходит прямая, параллельная данной и притом только одна
Слайд 6
ВСПОМНИМ ПЛАНИМЕТРИЮ
Следствия аксиомы параллельных прямых - ?
Если прямая пересекает одну
из параллельных прямых, то она пересекает и другую.
Если две прямые
параллельны третьей прямой, то они параллельны.
Слайд 7Аксиомы стереометрии
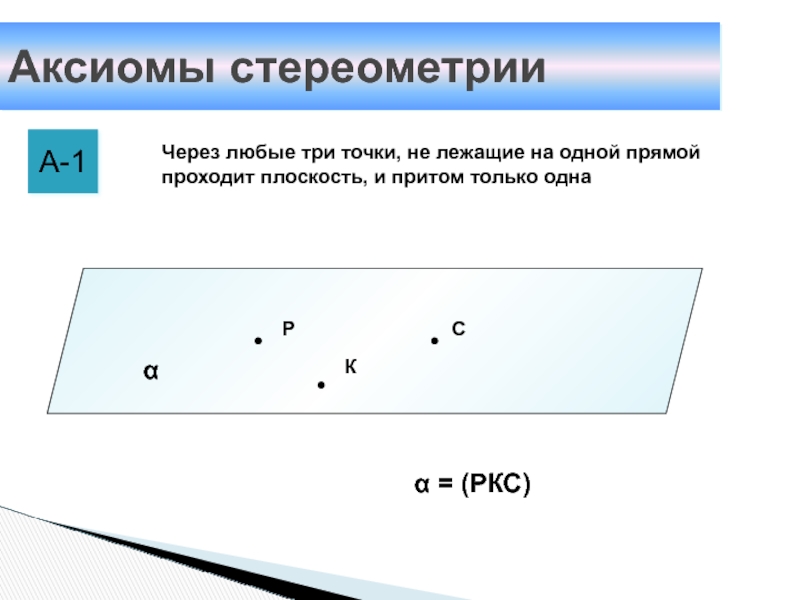
А-1
Через любые три точки, не лежащие на одной прямой
проходит плоскость, и притом только одна
α = (РКС)
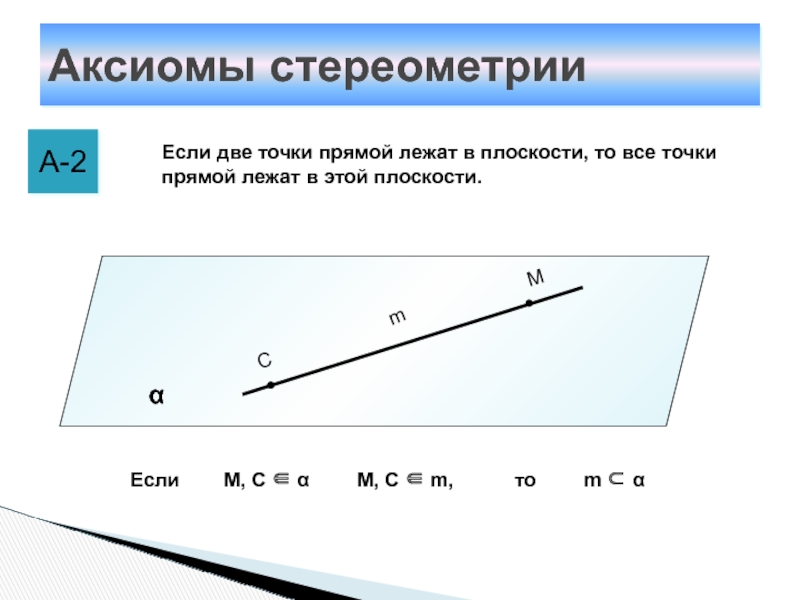
Слайд 8Аксиомы стереометрии
А-2
Если две точки прямой лежат в плоскости, то все
точки прямой лежат в этой плоскости.
m
М, C ∈ α
m
⊂ αМ, C ∈ m,
Если
то
Слайд 9Аксиомы стереометрии
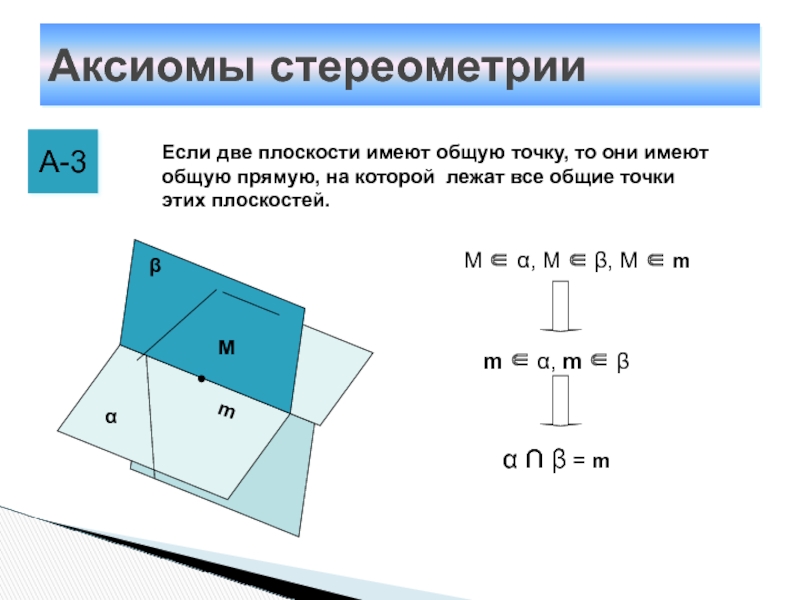
А-3
Если две плоскости имеют общую точку, то они имеют
общую прямую, на которой лежат все общие точки этих плоскостей.
М
∈ α, М ∈ β, М ∈ mm ∈ α, m ∈ β
α ∩ β = m
Слайд 10СЛЕДСТВИЯ ИЗ АКСИОМ
Т-1
Через любую прямую и не принадлежащую ей точку
можно провести плоскость, и притом только одну.
м
А
В
Дано: М∉m
Так как
М∉m, то точки А, В и M не принадлежат одной прямой.
По А-1 через точки А, В и M проходит только одна плоскость — плоскость (ABM), Обозначим её α. Прямая m имеет с ней две общие точки — точки A и B, следовательно, по аксиоме А-2 эта прямая лежит в плоскости α..
Таким образом, плоскость α проходит через прямую m и точку M и является искомой.
Докажем, что другой плоскости, проходящей через прямую m и точку M, не существует. Предположим, что есть другая плоскость — β, проходящая через прямую m и точку M. Тогда плоскости α и β проходят через точки А, В и M, не принадлежащие одной прямой, а значит, совпадают. Следовательно, плоскость α единственна.
Теорема доказана
Доказательство
Пусть точки A, B ∈ m.
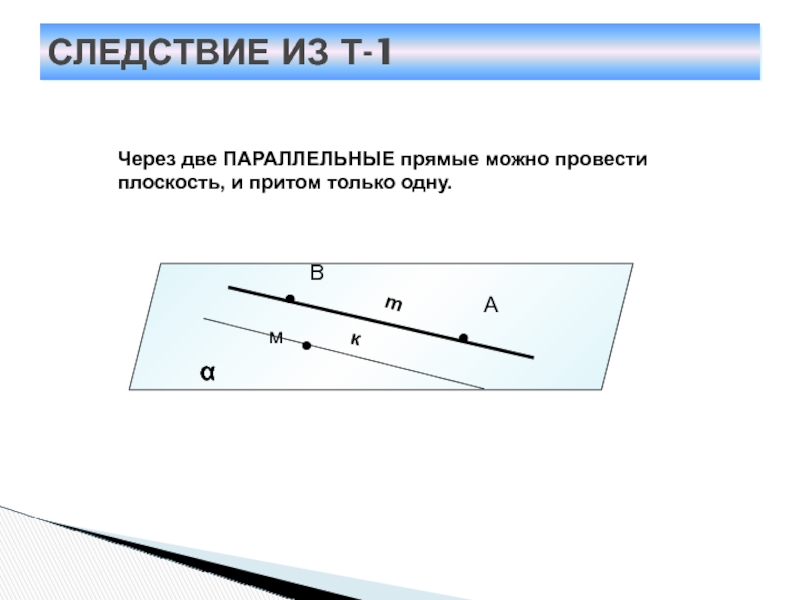
Слайд 11СЛЕДСТВИЕ ИЗ Т-1
Через две ПАРАЛЛЕЛЬНЫЕ прямые можно провести плоскость, и
притом только одну.
к
Слайд 12СЛЕДСТВИЯ ИЗ АКСИОМ
Т-2
Через любые две пересекающиеся прямые можно провести плоскость,
и притом только одну.
N
Дано: m ∩ n = M
Доказательство
Отметим
на прямой m произвольную точку N, отличную от М. Рассмотрим плоскость α =(n, N). Так как M∈ α и N∈α, то по А-2 m ⊂ α. Значит обе прямые m, n лежат в плоскости α и следовательно α, является искомой
Докажем единственность плоскости α. Допустим, что есть другая, отличная от плоскости α и проходящая через прямые m и n, плоскость β.
Так как плоскость β проходит через прямую n и не принадлежащую ей точку N, то по T-1 она совпадает с плоскостью α. Единственность плоскости α доказана.
Теорема доказана
Слайд 13По трем точкам, не лежащим на одной прямой
По прямой и
точке, не лежащей на этой прямой
По двум пересекающимся прямым
По двум
параллельным прямымВЫВОД
Как в пространстве можно однозначно задать плоскость?
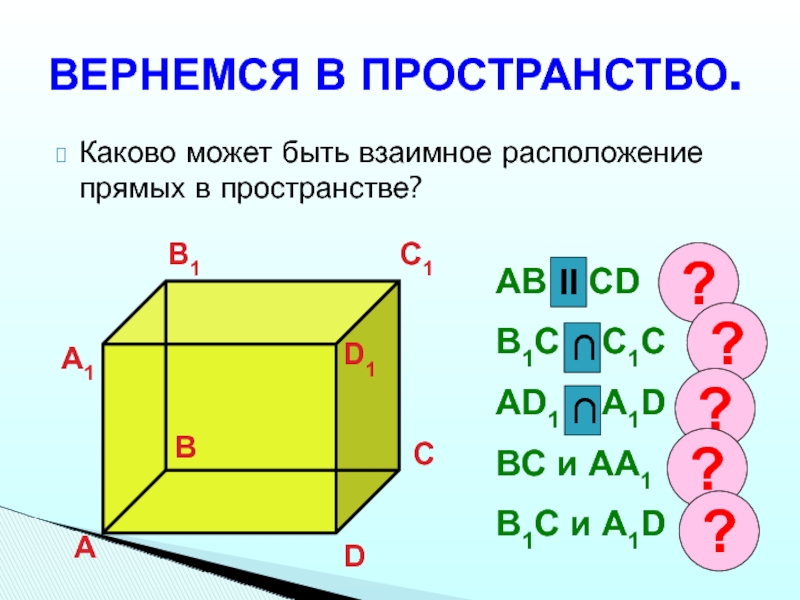
Слайд 14ВЕРНЕМСЯ В ПРОСТРАНСТВО.
Каково может быть взаимное расположение прямых в пространстве?
А
B
C
D
А1
B1
C1
D1
AB
и CD
B1C и C1C
AD1 и A1D
BC и AA1
B1C и A1D
II
?
∩
?
∩
?
?
?
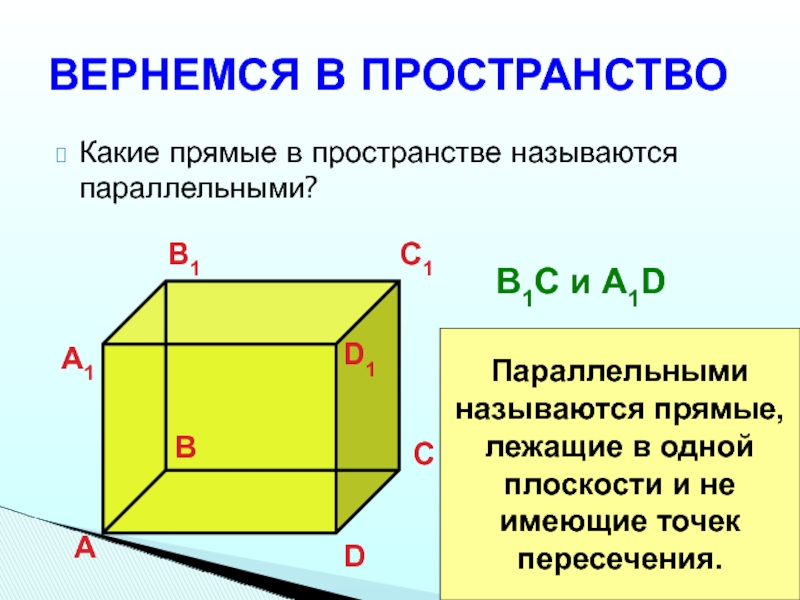
Слайд 15ВЕРНЕМСЯ В ПРОСТРАНСТВО
Какие прямые в пространстве называются параллельными?
А
B
C
D
А1
B1
C1
D1
B1C и A1D
Параллельными
называются прямые,
лежащие в одной
плоскости и не
имеющие точек
пересечения.
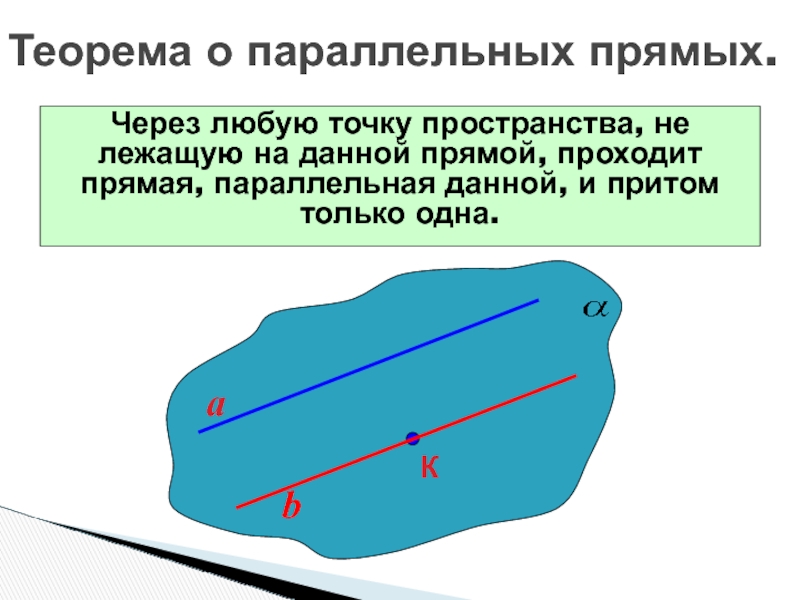
Слайд 16
Теорема о параллельных прямых.
Через любую точку пространства, не лежащую на
данной прямой, проходит прямая, параллельная данной, и притом только одна.
К
a
b
Слайд 17…они лежат на параллельных прямых
Отрезки в пространстве называются параллельными, если
…
Лучи в пространстве называются параллельными, если …
Параллельные отрезки,
параллельные лучи
в пространстве.
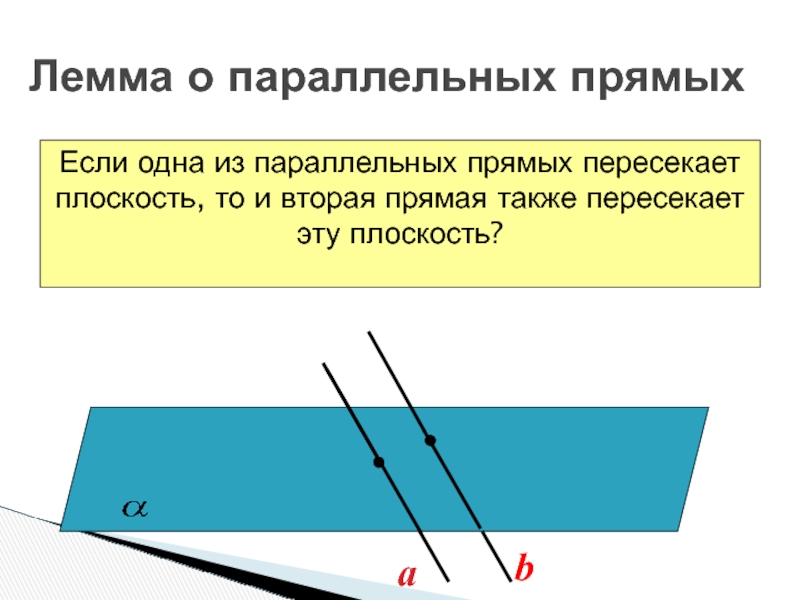
Слайд 18
Лемма о параллельных прямых
Если одна из параллельных прямых пересекает плоскость,
то и вторая прямая также пересекает эту плоскость?
a
b
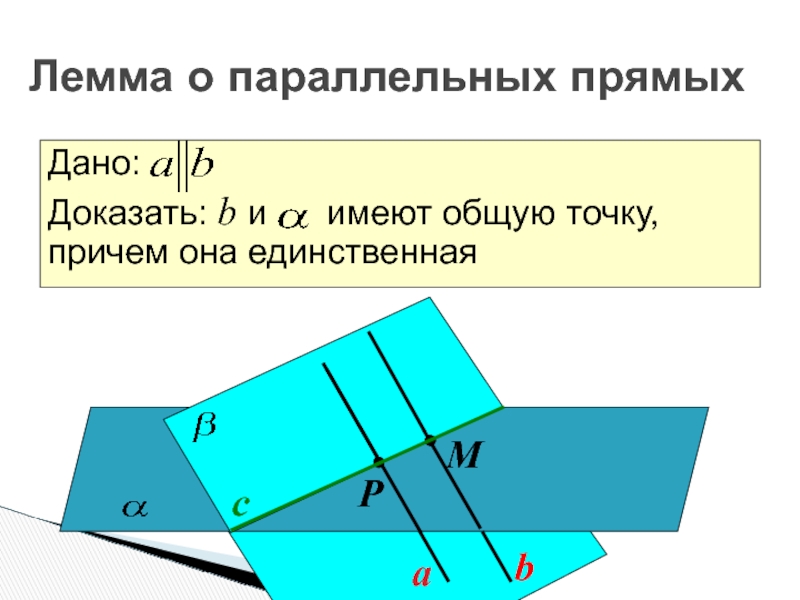
Слайд 20
a
b
с
Р
М
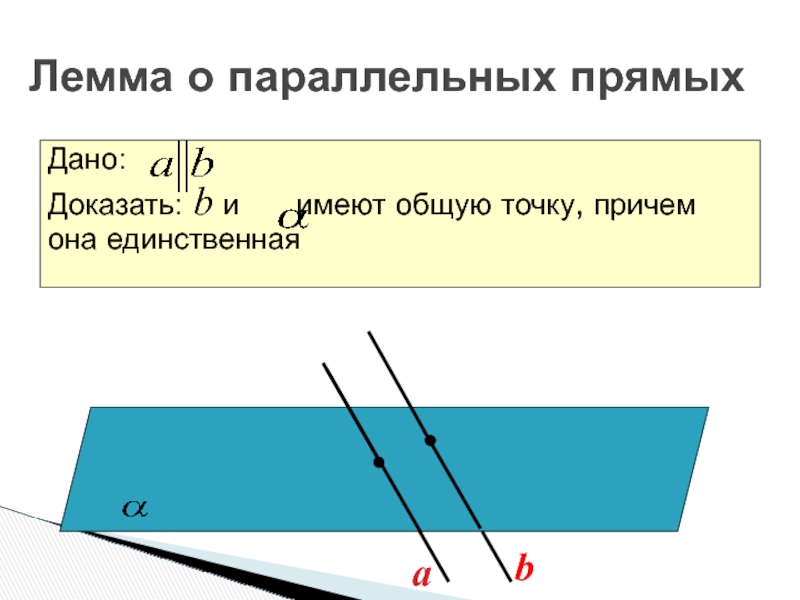
Дано:
Доказать: b и имеют общую точку, причем
она единственная
Лемма о параллельных прямых
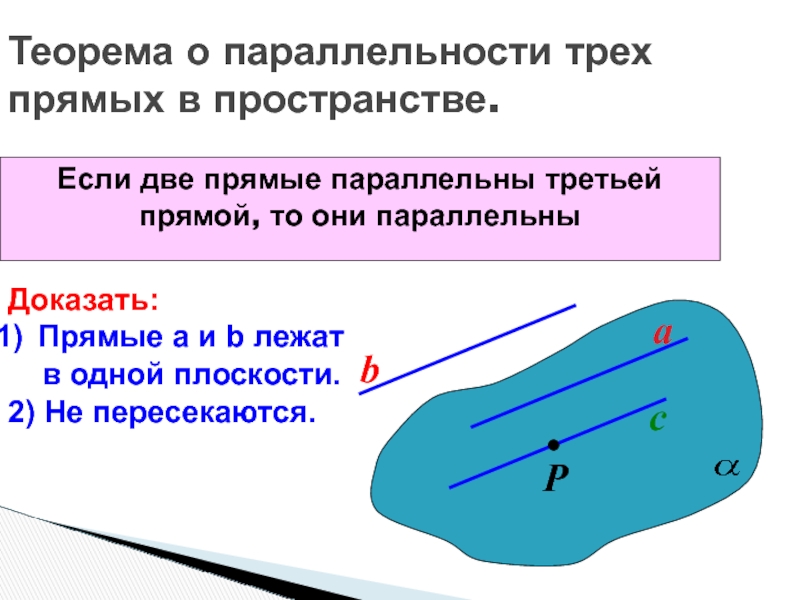
Слайд 21Теорема о параллельности трех прямых в пространстве.
Если две прямые параллельны
третьей прямой, то они параллельны
a
b
с
Дано:
Доказать:
и
Слайд 22Теорема о параллельности трех прямых в пространстве.
Если две прямые параллельны
третьей прямой, то они параллельны
a
b
с
Р
Доказать:
Прямые а и b лежат
в одной плоскости.2) Не пересекаются.
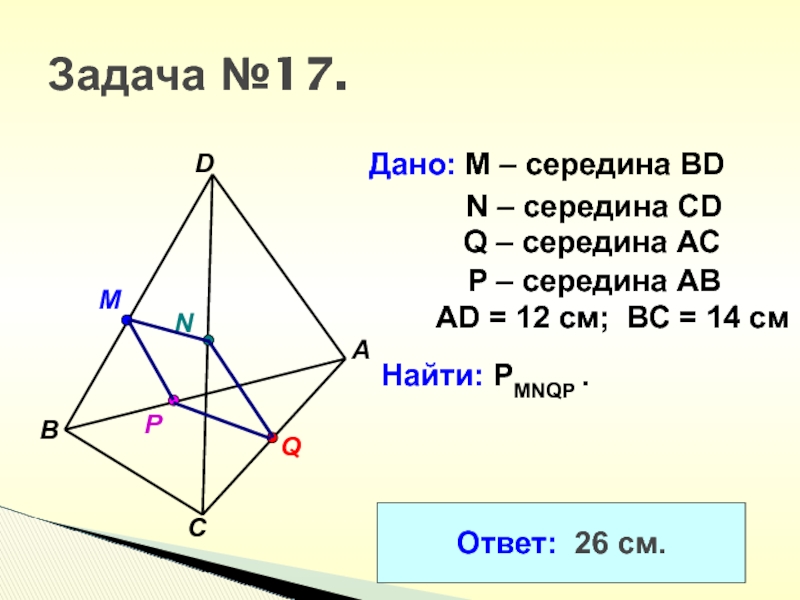
Слайд 23Задача №17.
Дано: М – середина BD
A
B
D
C
N
M
Р
Q
N – середина CD
Q
– середина АС
P – середина АВ
АD = 12 см; ВС
= 14 смНайти: PMNQP .
Ответ: 26 см.
Слайд 26Построение прямой, не пересекающей плоскость.
α
1. Проведем плоскость α.
2. В данной
плоскости
проведем прямую а1.
а1
3. Возьмем вне плоскости
т.АА
4. Через точку А и прямую а1
проведем плоскость β
β
5. В плоскости β через точку А
проведем прямую а парал-
лельную прямой а1.
а
а – искомая прямая.
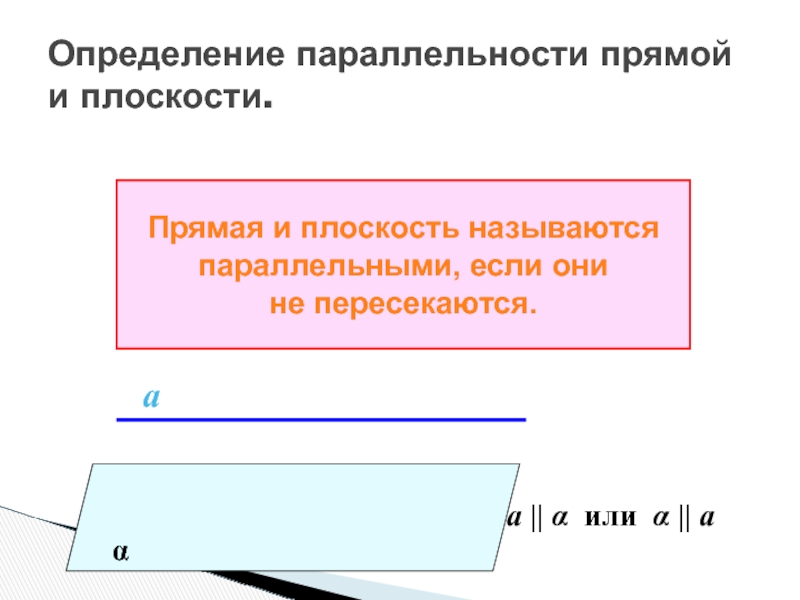
Слайд 27Построение прямой, не пересекающей плоскость.
α
а1
А
β
а
Доказательство:
1) Пусть а ∩ α =
B.
В
2) β ∩ α = а1
В
€ βВ € α
В € а1, т.е.
а ∩ а1=В, что
противоречит
построению
( а || а1 )
а и α не пересекаются.
ч.т.д.
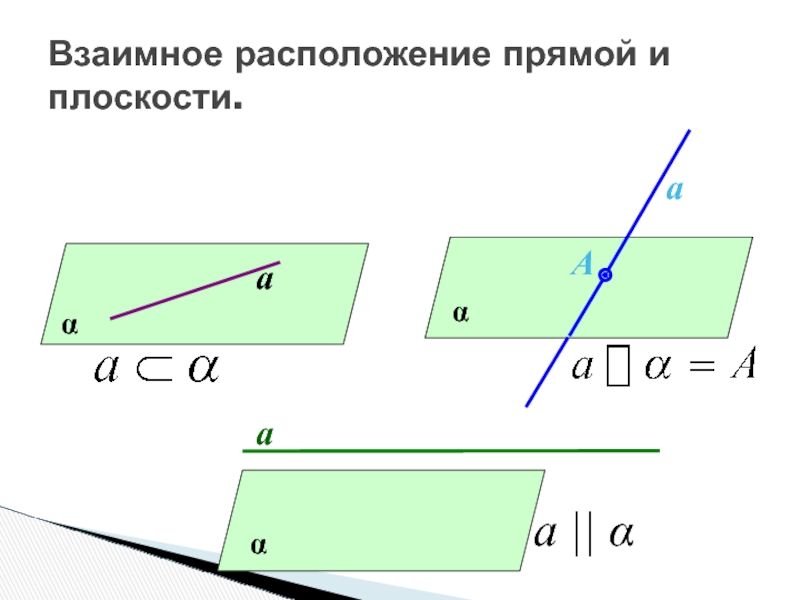
Слайд 28Определение параллельности прямой и плоскости.
Прямая и плоскость называются
параллельными, если
они
не пересекаются.
α
а
а || α или α || а
Слайд 30Построение параллельных прямой и плоскости.
а1
а
α
а || а1
а || α
Признак параллельности
прямой и плоскости.
Если прямая, не лежащая в данной
плоскости, параллельна какой-нибудь
прямой
в этой плоскости, то она параллельна и самой плоскости.
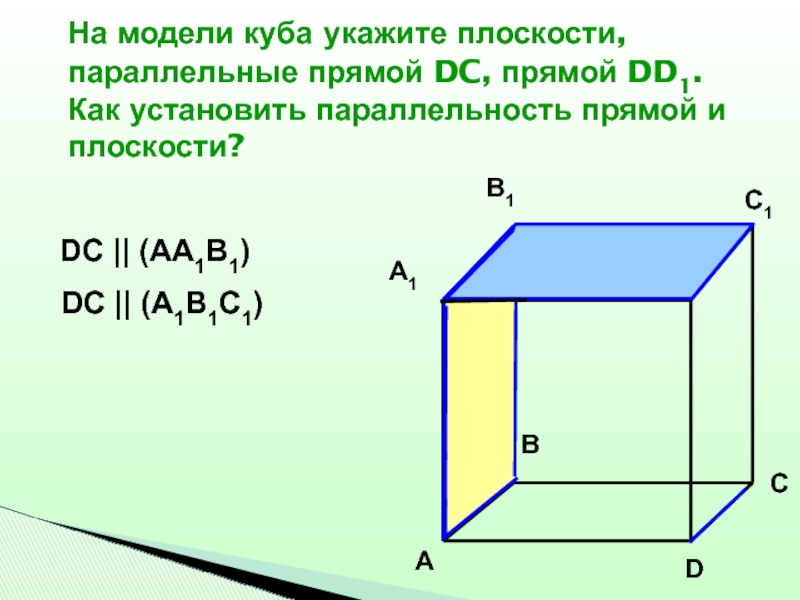
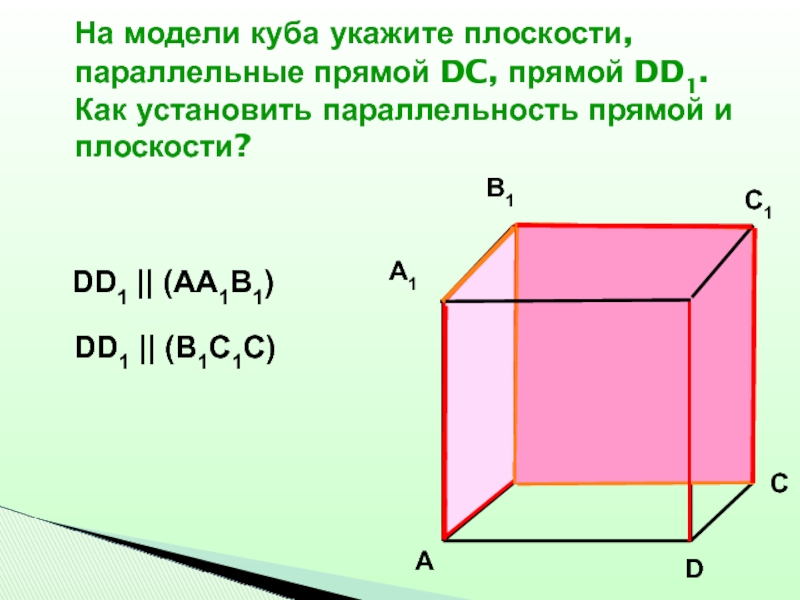
Слайд 31На модели куба укажите плоскости, параллельные прямой DC, прямой DD1. Как
установить параллельность прямой и плоскости?
C1
C
DC || (AA1B1)
DC || (A1B1C1)
Слайд 32На модели куба укажите плоскости, параллельные прямой DC, прямой DD1. Как
установить параллельность прямой и плоскости?
C1
C
DD1 || (AA1B1)
DD1 || (B1C1C)
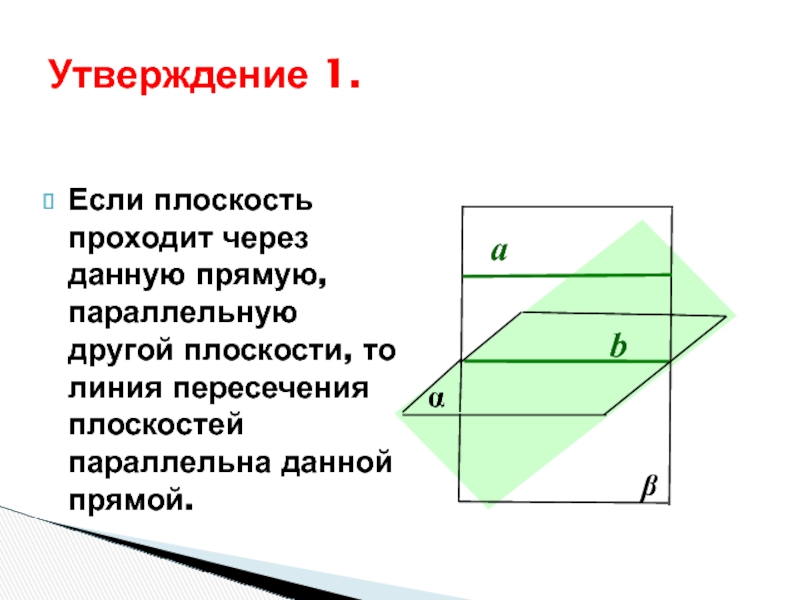
Слайд 33Если плоскость проходит через данную прямую, параллельную другой плоскости, то
линия пересечения плоскостей параллельна данной прямой.
Утверждение 1.
α
β
а
b
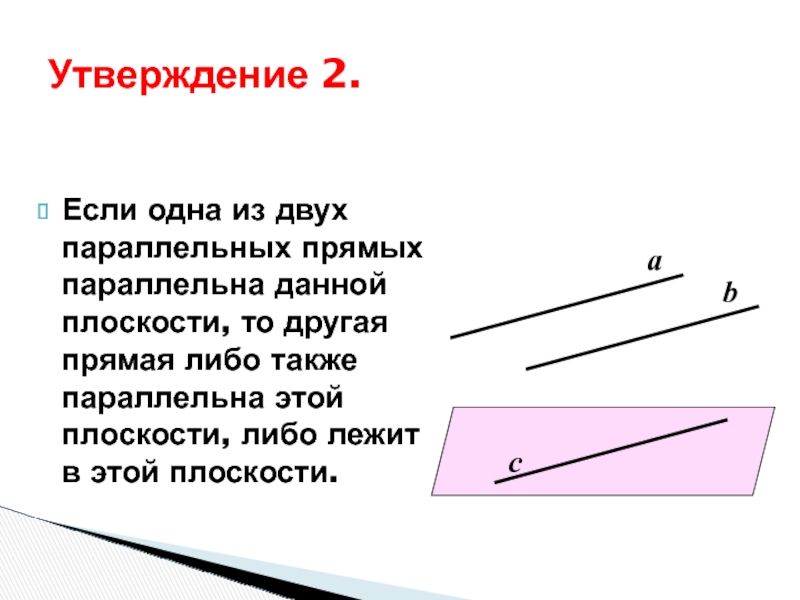
Слайд 34Если одна из двух параллельных прямых параллельна данной плоскости, то
другая прямая либо также параллельна этой плоскости, либо лежит в
этой плоскости.Утверждение 2.
а
b
с
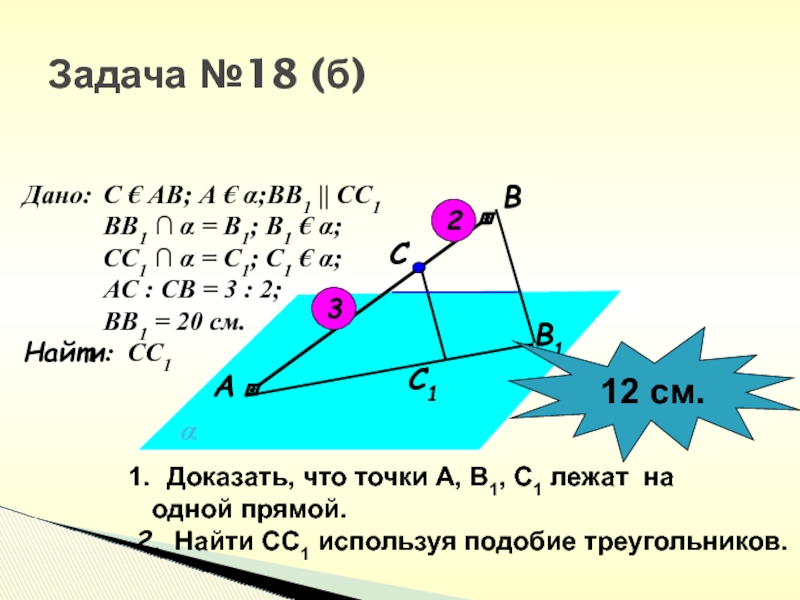
Слайд 35Задача №18 (б)
С1
В1
С
В
А
α
Доказать, что точки А, В1, С1 лежат на
одной прямой.
Дано: С € АВ; А € α;ВВ1 ||
СС1ВВ1 ∩ α = В1; В1 € α;
СС1 ∩ α = С1; С1 € α;
АС : СВ = 3 : 2;
ВВ1 = 20 см.
Найти: СС1
2. Найти СС1 используя подобие треугольников.
12 см.
3
2
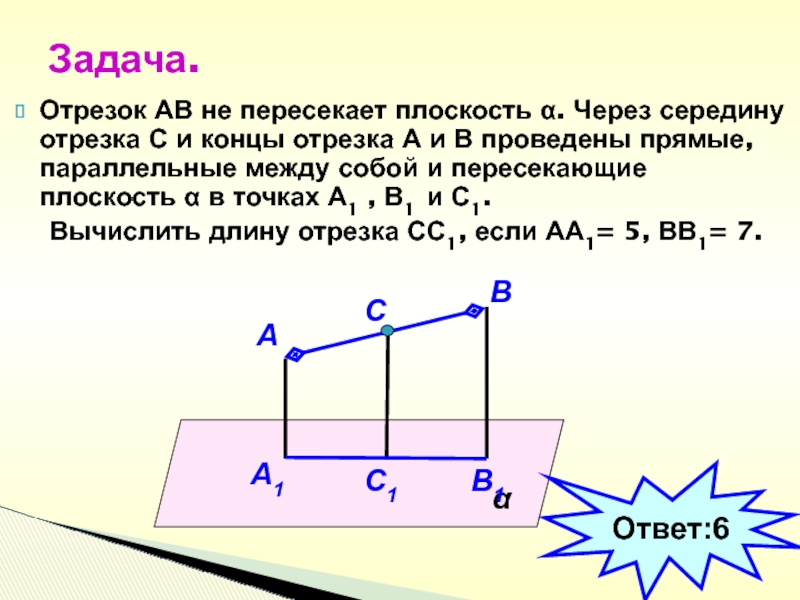
Слайд 37Отрезок АВ не пересекает плоскость α. Через середину отрезка С
и концы отрезка А и В проведены прямые, параллельные между
собой и пересекающие плоскость α в точках А1 , В1 и С1.Вычислить длину отрезка СС1, если АА1= 5, ВВ1= 7.
Задача.
α
А
В
С
А1
В1
С1
Ответ:6
Слайд 38Точка М лежит на отрезке АВ. Отрезок АВ пересекает плоскость
α в точке В. Через А и В проведены параллельные
прямые, пересекающие α в точках А1 и М1.Задача.
α
А
В
М
А1
М1
а) Докажите, что А1, М1 и В
лежат на одной прямой.
б) Найдите длину отрезка
АВ, если АА1 : ММ1 = 3 : 2,
АМ = 6.
Ответ:12
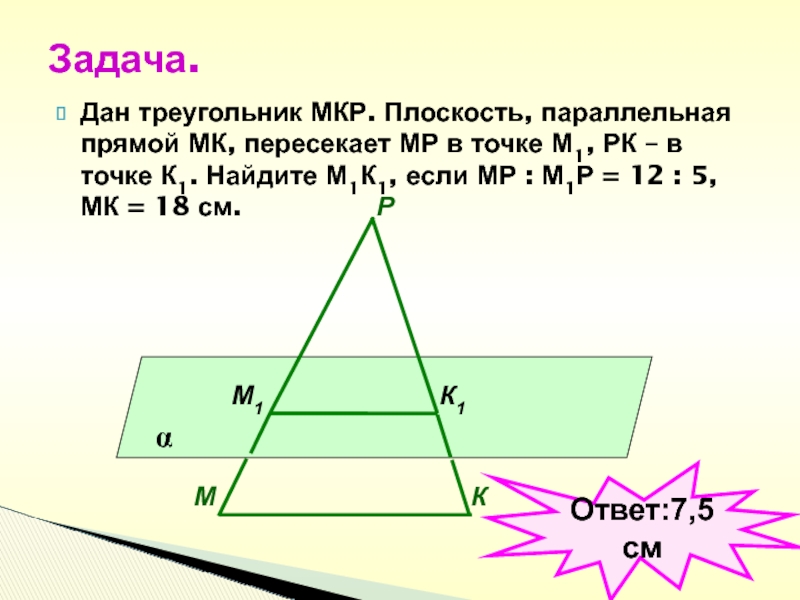
Слайд 39Дан треугольник МКР. Плоскость, параллельная прямой МК, пересекает МР в
точке М1, РК – в точке К1. Найдите М1К1, если
МР : М1Р = 12 : 5, МК = 18 см.Задача.
α
М
К
Р
М1
К1
Ответ:7,5 см
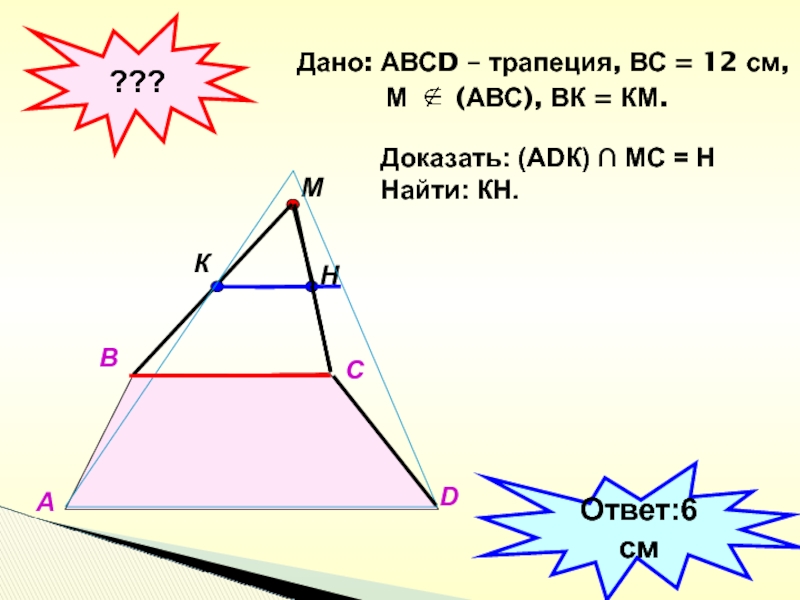
Слайд 40Дано: АВСD – трапеция, ВС = 12 см,
М (АВС), ВК =
КМ.???
А
В
С
D
М
К
Доказать: (АDК) ∩ МС = Н
Найти: КН.
Н
Ответ:6 см
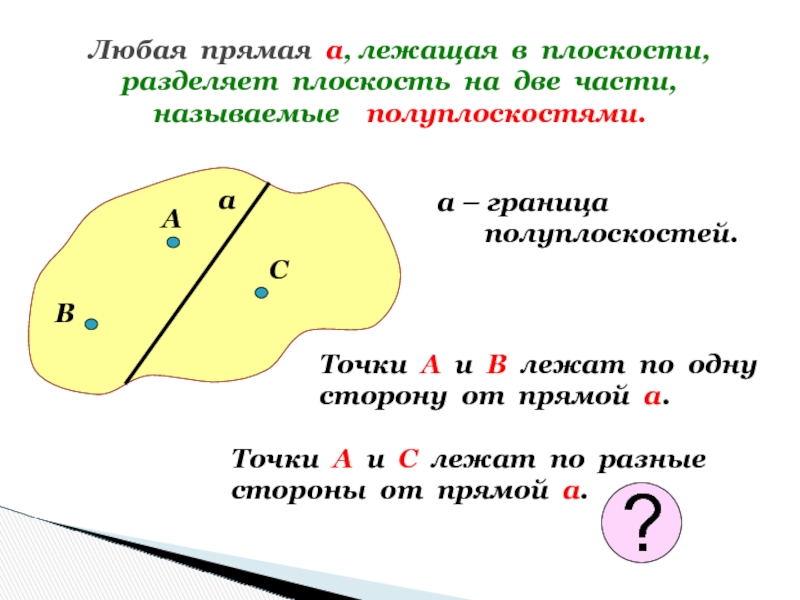
Слайд 47Любая прямая а, лежащая в плоскости, разделяет плоскость на две
части, называемые полуплоскостями.
а
а – граница
полуплоскостей.А
В
С
Точки А и В лежат по одну
сторону от прямой а.
Точки А и С лежат по разные
стороны от прямой а.
?
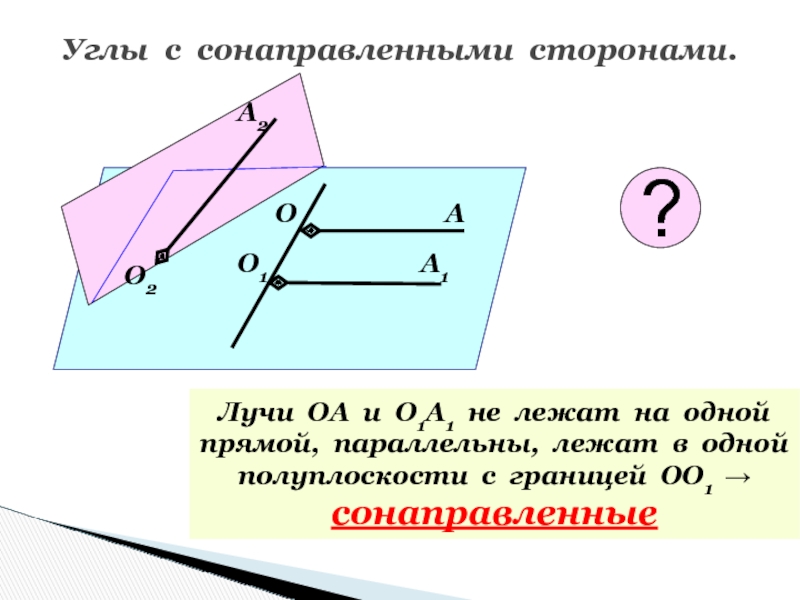
Слайд 48Углы с сонаправленными сторонами.
О
А
О1
А1
Лучи ОА и О1А1 не лежат на
одной
прямой, параллельны, лежат в одной
полуплоскости с границей ОО1 →
сонаправленные
А2
О2
?
Слайд 49Теорема об углах
с сонаправленными сторонами
Если стороны двух углов
соответственно
сонаправлены, то такие углы равны.
О1
О
А1
В1
В
А
Дано: угол О и угол
О1с сонаправленными
сторонами.
Доказать:
Слайд 50Теорема об углах
с сонаправленными сторонами
О1
О
А1
В1
В
А
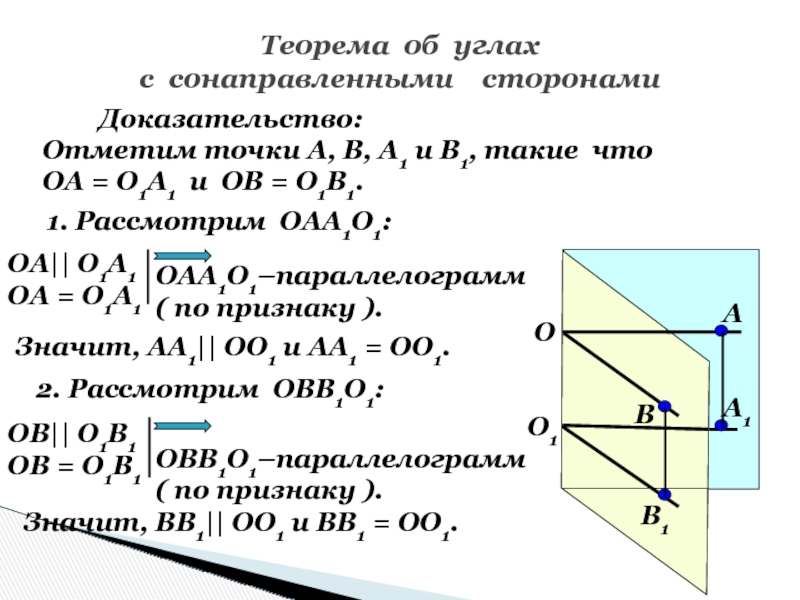
Доказательство:
Отметим точки А, В,
А1 и В1, такие что
ОА = О1А1 и ОВ =
О1В1.1. Рассмотрим ОАА1О1:
ОА|| О1А1
ОА = О1А1
ОАА1О1–параллелограмм
( по признаку ).
2. Рассмотрим ОВВ1О1:
Значит, АА1|| ОО1 и АА1 = ОО1.
ОВ|| О1В1
ОВ = О1В1
ОВВ1О1–параллелограмм
( по признаку ).
Значит, ВВ1|| ОО1 и ВВ1 = ОО1.
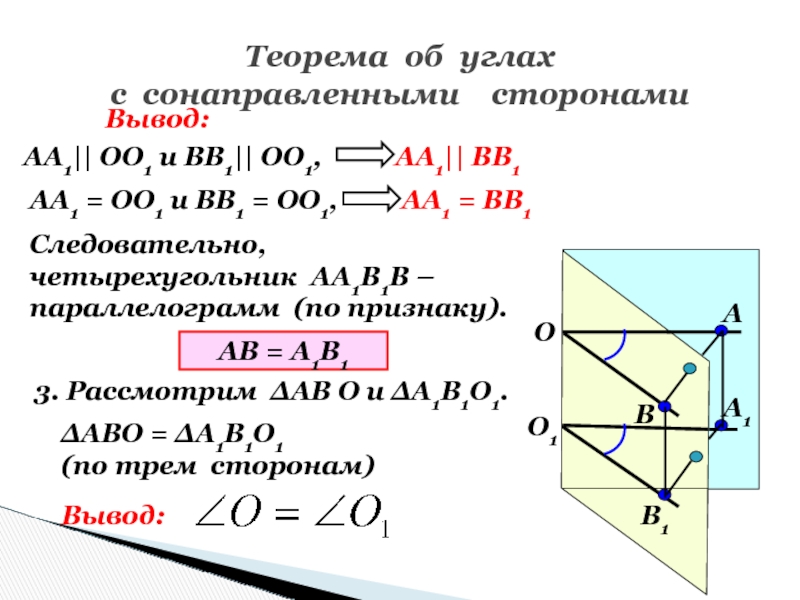
Слайд 51Теорема об углах
с сонаправленными сторонами
О1
О
А1
В1
В
А
Вывод:
АА1|| ОО1 и ВВ1||
ОО1,
АА1|| ВВ1
АА1 = ОО1 и ВВ1 = ОО1,
АА1
= ВВ1Следовательно,
четырехугольник АА1В1В –
параллелограмм (по признаку).
АВ = А1В1
3. Рассмотрим ∆АВ О и ∆А1В1О1.
∆АВО = ∆А1В1О1
(по трем сторонам)
Вывод:
Слайд 52Угол между скрещивающимися прямыми.
α
1800 - α
00 < α
900
1.
2.
Угол междускрещивающимися
прямыми АВ и СD
определяется как угол
между пересекающимися
прямыми А1В1 и С1D1,
при этом А1В1|| АВ и С1D1|| CD.
А
В
D
С
А1
В1
С1
D1
α
М1
Слайд 53Практическое задание.
Выбрать любую точку М2.
Построить А2В2|| АВ и С2D2|| CD.
Ответить
на вопросы:
1. Почему А2В2|| А1В1 и С2D2|| C1D1?
2. Являются ли
углы А1М1D1 и А2М2D2 углами с соответственно
параллельными сторонами?
?
Вывод:
1.
Величина угла между скрещивающимися
прямыми не зависит от выбора точки.
3.
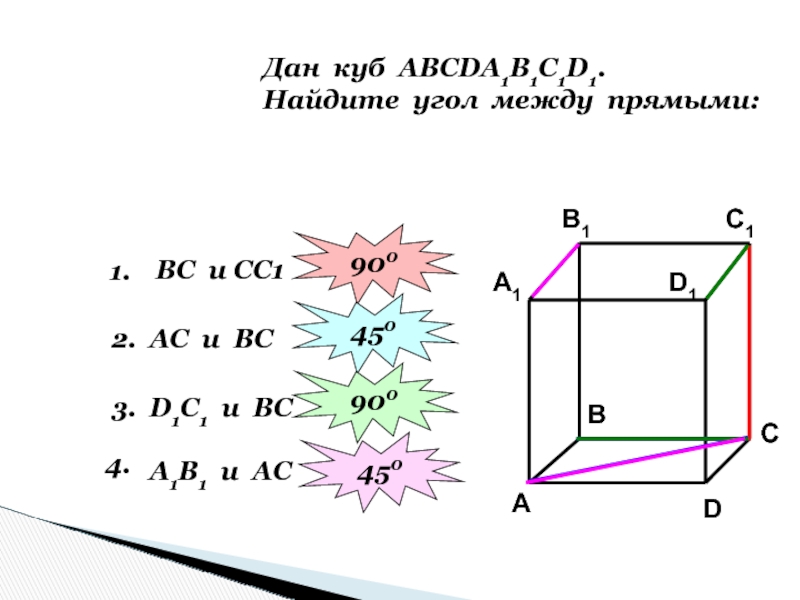
Слайд 54Дан куб АВСDА1В1С1D1.
Найдите угол между прямыми:
1.
ВС и СС1
2.
900
АС и ВС
450
3.
D1С1
и ВС
900
4.
А1В1 и АС
450
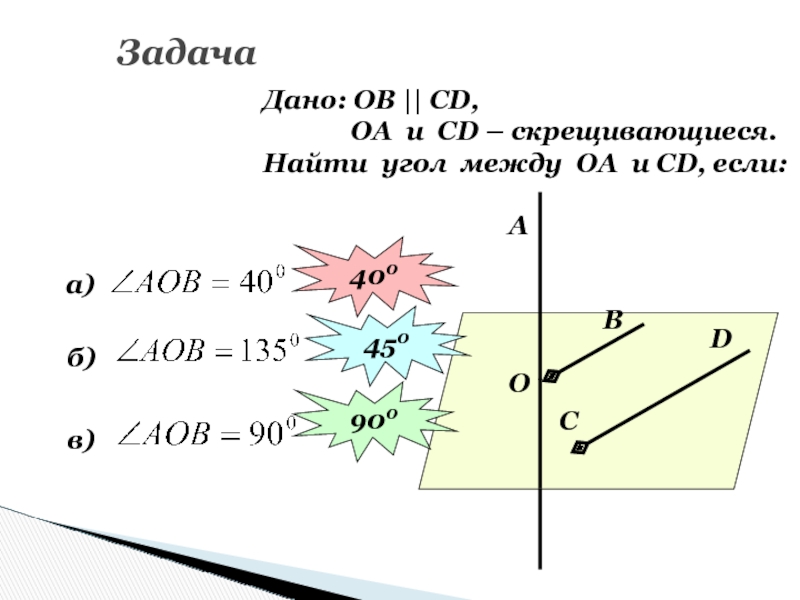
Слайд 55Задача
Дано: ОВ || СD,
ОА и СD – скрещивающиеся.
Найти угол между ОА и СD,
если:О
В
C
D
A
а)
400
б)
450
в)
900
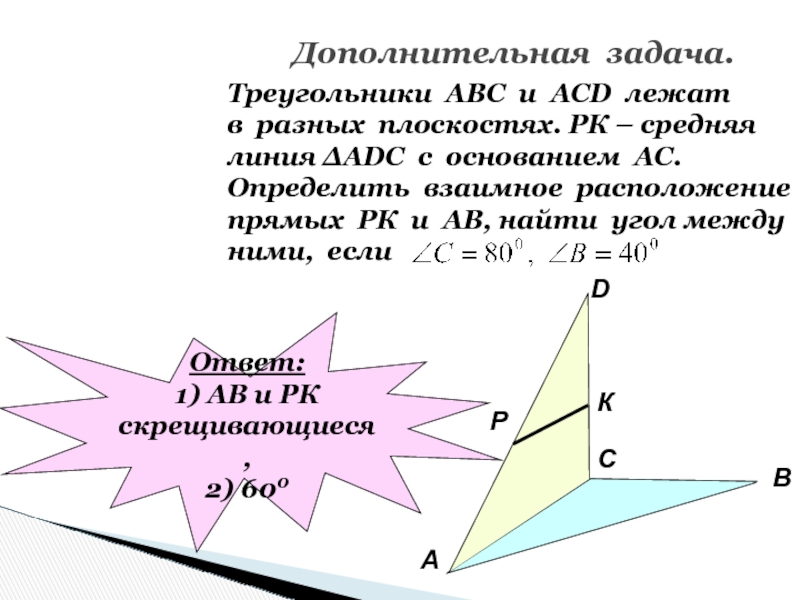
Слайд 56Дополнительная задача.
Треугольники АВС и АСD лежат
в разных плоскостях. РК –
средняя
линия ∆АDC с основанием АС.
Определить взаимное расположение
прямых РК и АВ,
найти угол междуними, если
А
В
С
D
P
К
Ответ:
1) АВ и РК скрещивающиеся,
2) 600
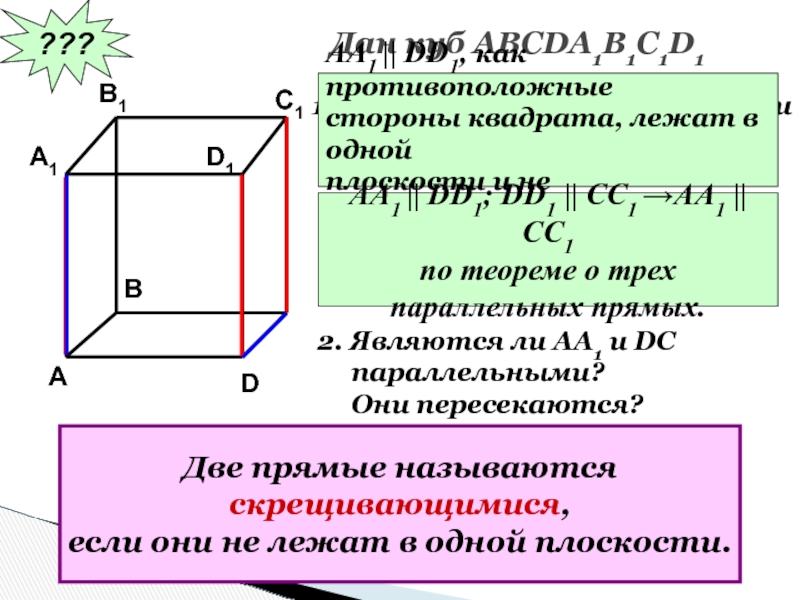
Слайд 59???
Дан куб АВСDA1B1C1D1
Являются ли параллельными
прямые АА1 и DD1;
АА1 и СС1 ?
Почему?
АА1 || DD1, как противоположные
стороны
квадрата, лежат в однойплоскости и не пересекаются.
АА1 || DD1; DD1 || CC1 →AA1 || CC1
по теореме о трех
параллельных прямых.
2. Являются ли АА1 и DC
параллельными?
Они пересекаются?
Две прямые называются
скрещивающимися,
если они не лежат в одной плоскости.
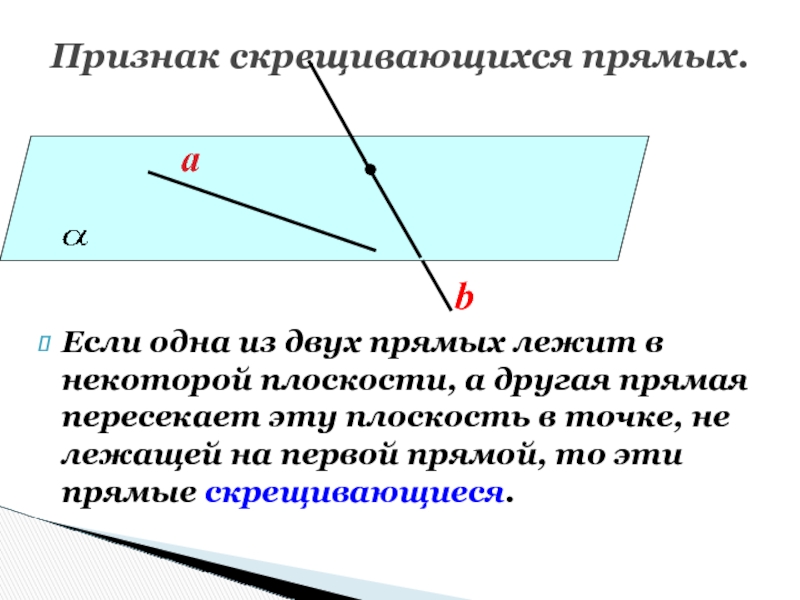
Слайд 60Признак скрещивающихся прямых.
Если одна из двух прямых лежит в некоторой
плоскости, а другая прямая пересекает эту плоскость в точке, не
лежащей на первой прямой, то эти прямые скрещивающиеся.a
b
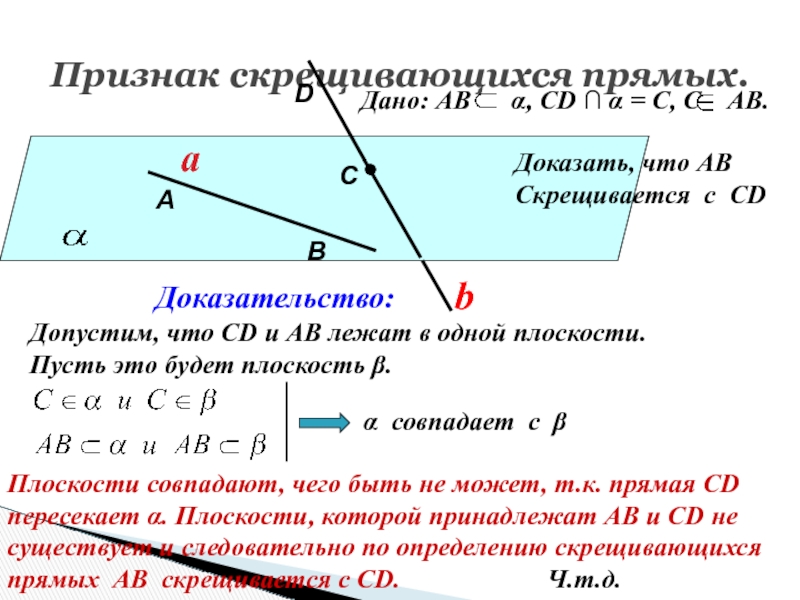
Слайд 61Признак скрещивающихся прямых.
Дано: АВ α, СD ∩ α
= С, С АВ.
a
b
Доказательство:
Допустим, что СD и АВ лежат
в одной плоскости. Пусть это будет плоскость β.
Доказать, что АВ
Скрещивается с СD
А
В
С
D
α совпадает с β
Плоскости совпадают, чего быть не может, т.к. прямая СD
пересекает α. Плоскости, которой принадлежат АВ и СD не
существует и следовательно по определению скрещивающихся
прямых АВ скрещивается с СD. Ч.т.д.
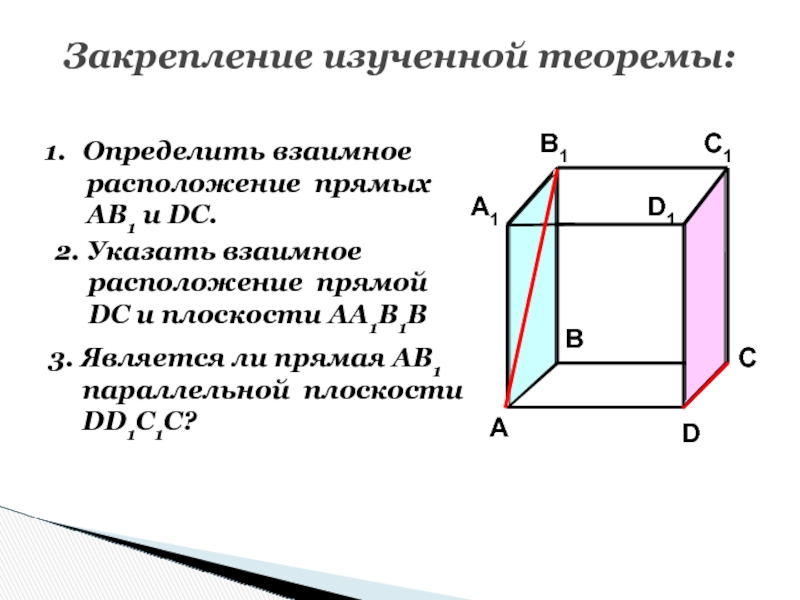
Слайд 62Закрепление изученной теоремы:
Определить взаимное
расположение прямых
АВ1 и DC.
2. Указать взаимное
расположение прямой
DC и плоскости АА1В1В3. Является ли прямая АВ1
параллельной плоскости
DD1С1С?
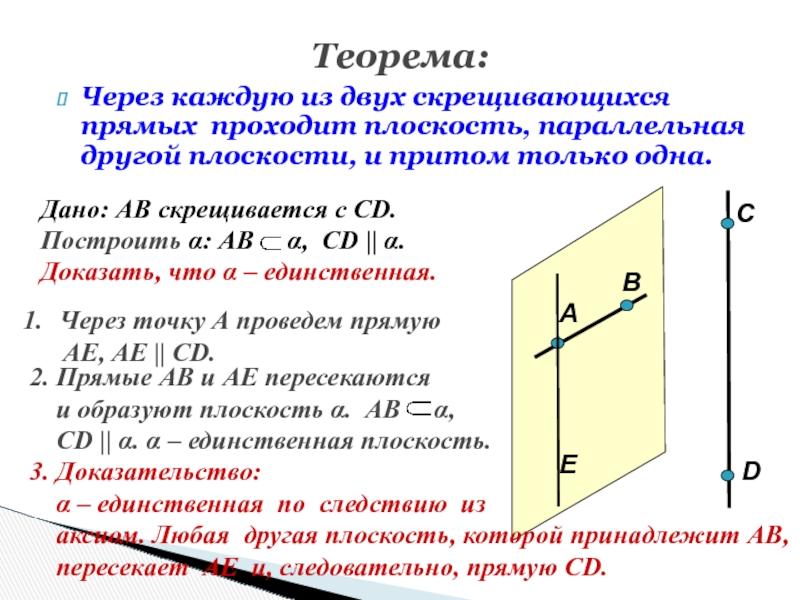
Слайд 63Теорема:
Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой
плоскости, и притом только одна.
Дано: АВ скрещивается с СD.
Построить α:
АВ α, СD || α.А
В
C
D
Через точку А проведем прямую
АЕ, АЕ || СD.
Е
2. Прямые АВ и АЕ пересекаются
и образуют плоскость α. АВ α,
СD || α. α – единственная плоскость.
Доказать, что α – единственная.
3. Доказательство:
α – единственная по следствию из
аксиом. Любая другая плоскость, которой принадлежит АВ,
пересекает АЕ и, следовательно, прямую СD.
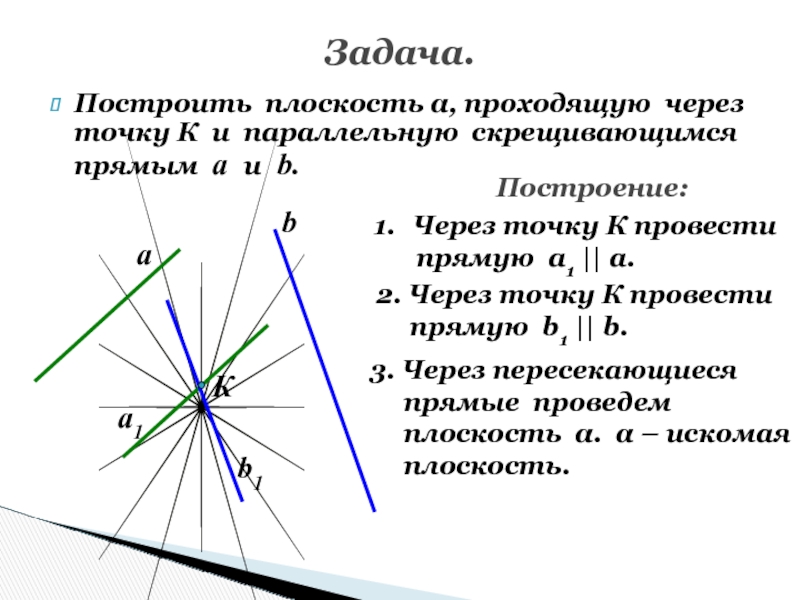
Слайд 64Задача.
Построить плоскость α, проходящую через точку К и параллельную скрещивающимся
прямым а и b.
Построение:
Через точку К провести
прямую
а1 || а.2. Через точку К провести
прямую b1 || b.
а
b
К
а1
b1
3. Через пересекающиеся
прямые проведем
плоскость α. α – искомая
плоскость.
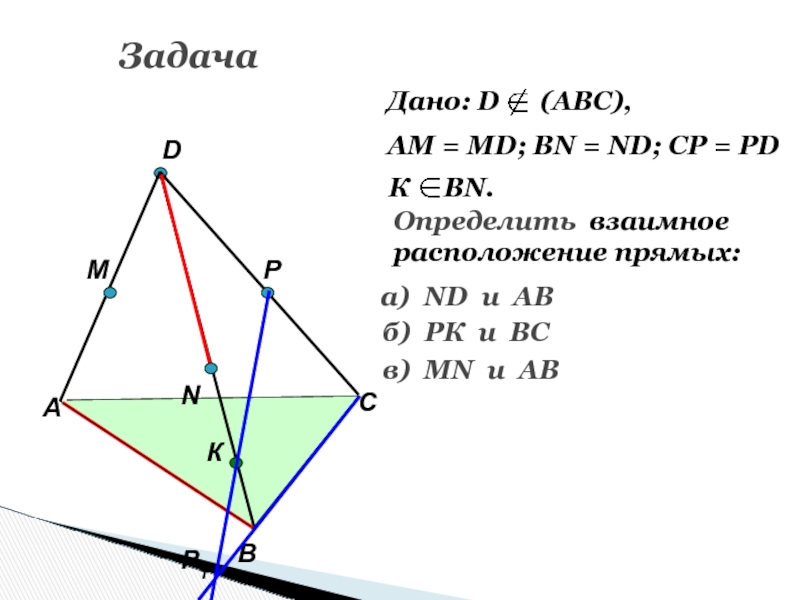
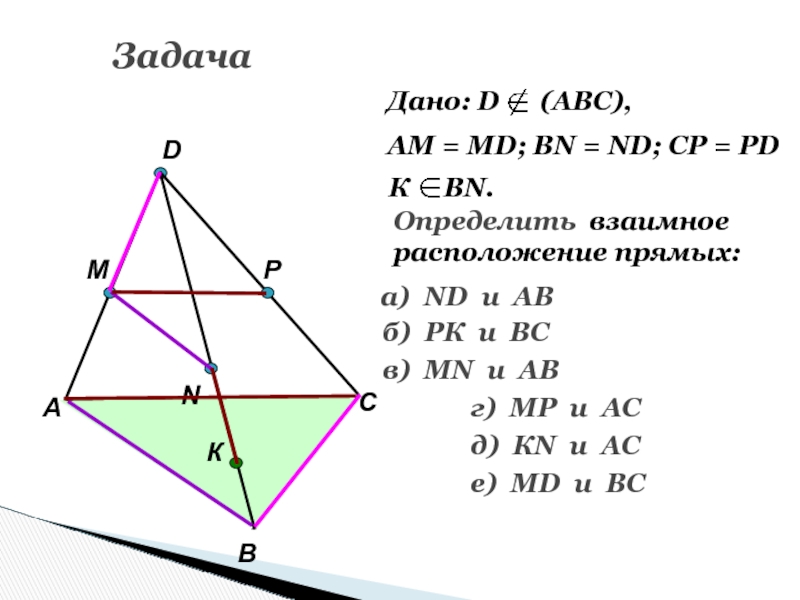
Слайд 65Задача
А
В
С
D
M
N
P
Р1
К
Дано: D (АВС),
АМ = МD; ВN = ND;
CP = PD
К ВN.
Определить взаимное
расположение прямых:
а) ND
и ABб) РК и ВС
в) МN и AB
Слайд 66Задача
А
В
С
D
M
N
P
К
Дано: D (АВС),
АМ = МD; ВN = ND;
CP = PD
К ВN.
Определить взаимное
расположение прямых:
а) ND
и ABб) РК и ВС
в) МN и AB
г) МР и AС
д) КN и AС
е) МD и BС
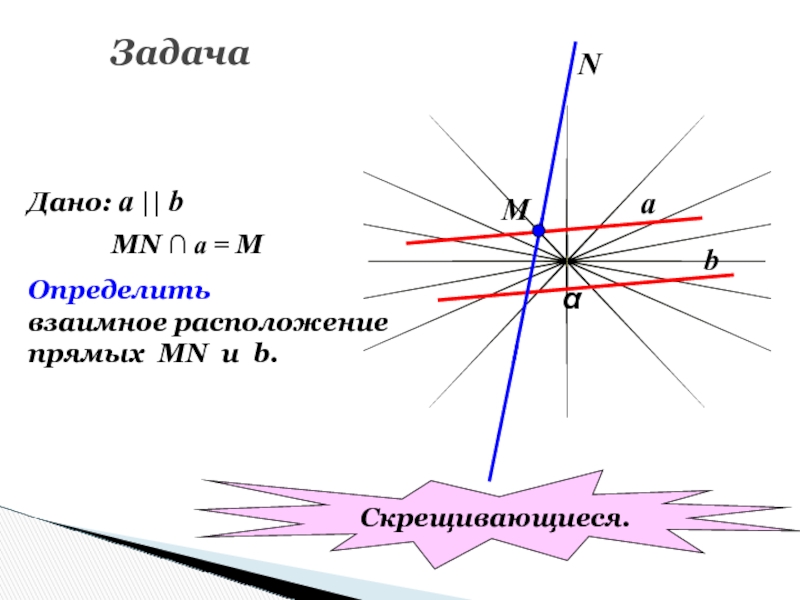
Слайд 67Задача
α
a
b
М
N
Дано: a || b
MN ∩ a = M
Определить
взаимное расположение
прямых MN
u b.
Скрещивающиеся.
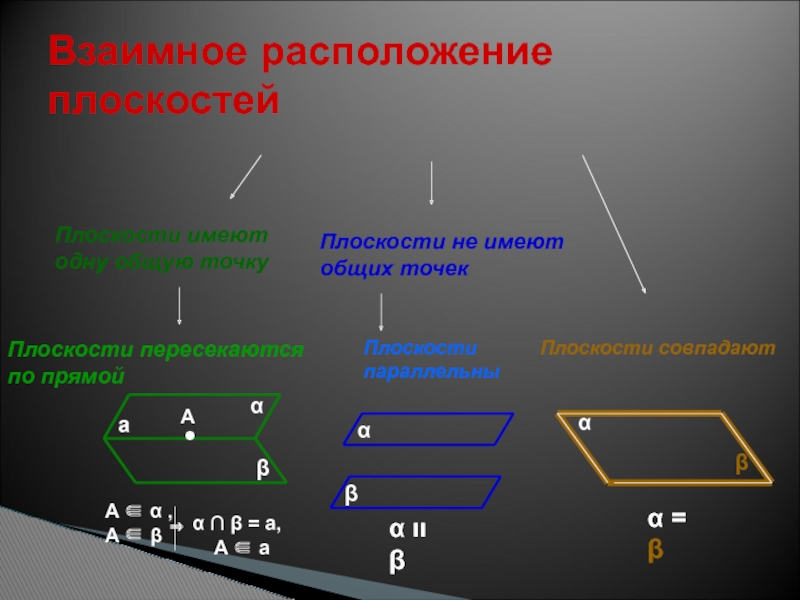
Слайд 68Взаимное расположение плоскостей
Плоскости имеют одну общую точку
Плоскости пересекаются по прямой
Плоскости
параллельны
α
β
a
.
A
A ∈ α ,
A ∈ β
α ∩
β = a,A ∈ a
α
β
α װ β
Плоскости не имеют общих точек
Плоскости совпадают
β
α
α = β
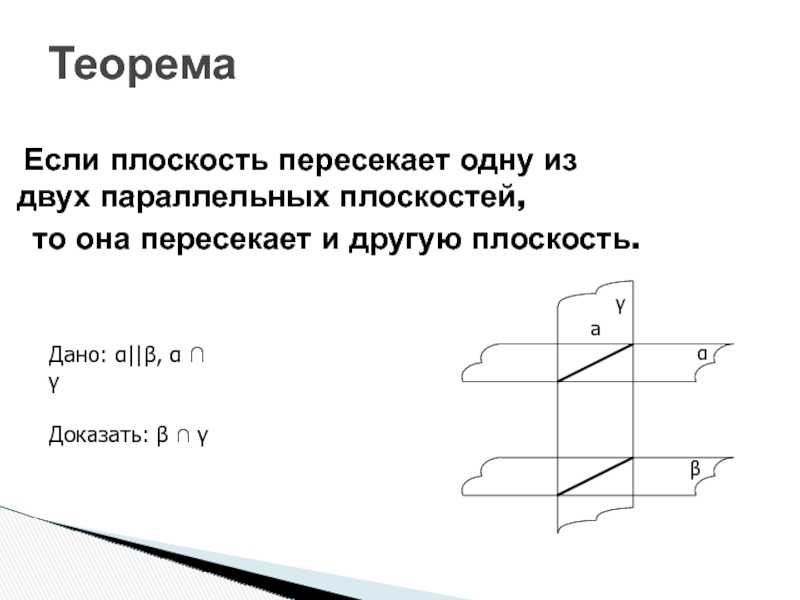
Слайд 70Теорема
Если плоскость пересекает одну из двух параллельных плоскостей,
то она пересекает и другую плоскость.
α
γ
β
а
Дано: α||β, α
∩ γДоказать: β ∩ γ
Слайд 71Доказательство
Проведём в плоскости γ прямую а, пересекающую плоскость α
в некоторой точке В.
Тогда по теореме: если
прямая пересекает одну из параллельных плоскостей, то она пересекает и другую плоскость. Значит прямая а пересекает β в некоторой точке А. Следовательно, плоскости β и γ
имеют общую точку А, т.е. пересекаются.
Теорема доказана
α
γ
β
В
А
а
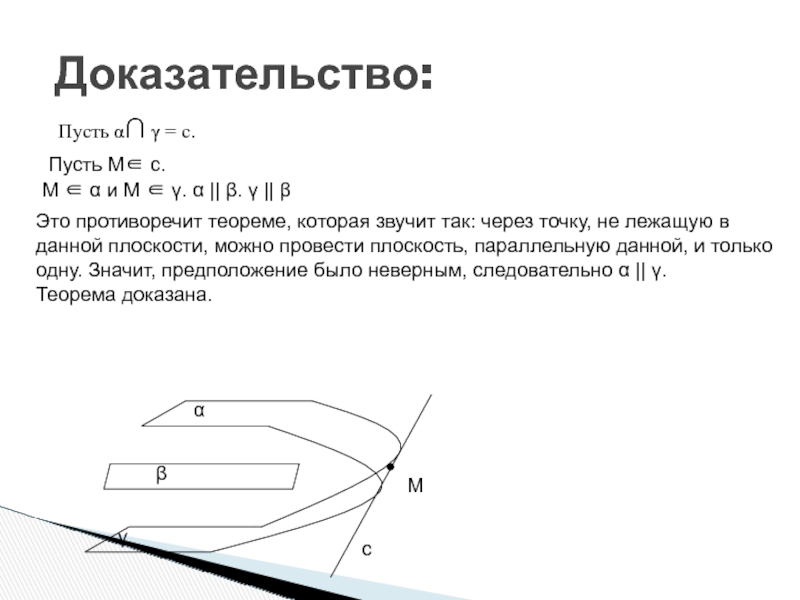
Слайд 73Доказательство:
Пусть α∩ γ = с.
с
α
β
γ
Пусть М∈ с.
М ∈ α
и М ∈ γ. α || β. γ || β
Это
противоречит теореме, которая звучит так: через точку, не лежащую в данной плоскости, можно провести плоскость, параллельную данной, и только одну. Значит, предположение было неверным, следовательно α || γ. Теорема доказана.
М
Слайд 74
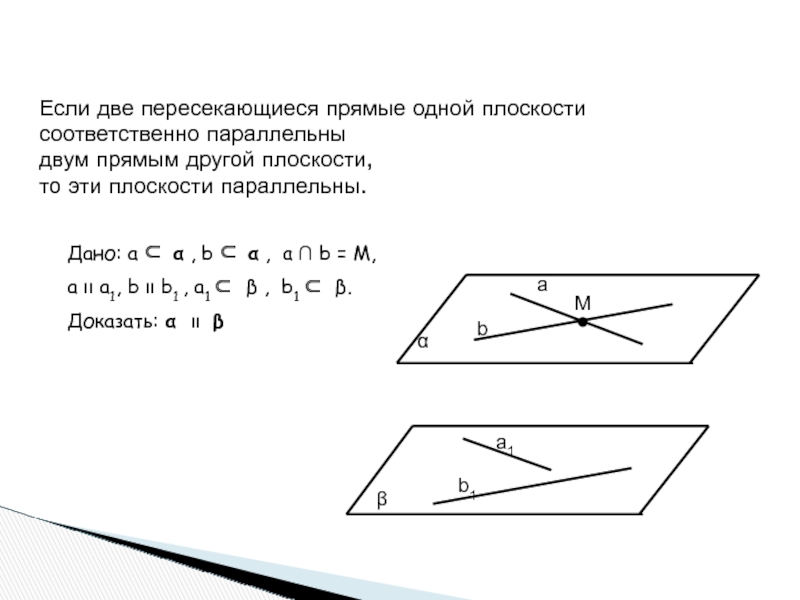
Если две пересекающиеся прямые одной плоскости
соответственно параллельны
двум прямым другой
плоскости,
то эти плоскости параллельны.
М
a
b
α
a1
b1
β
Дано: a ⊂ α , b ⊂ α , a ∩ b = M,
a װ a1, b װ b1 , a1 ⊂ β , b1 ⊂ β.
Доказать: α װ β
Слайд 75
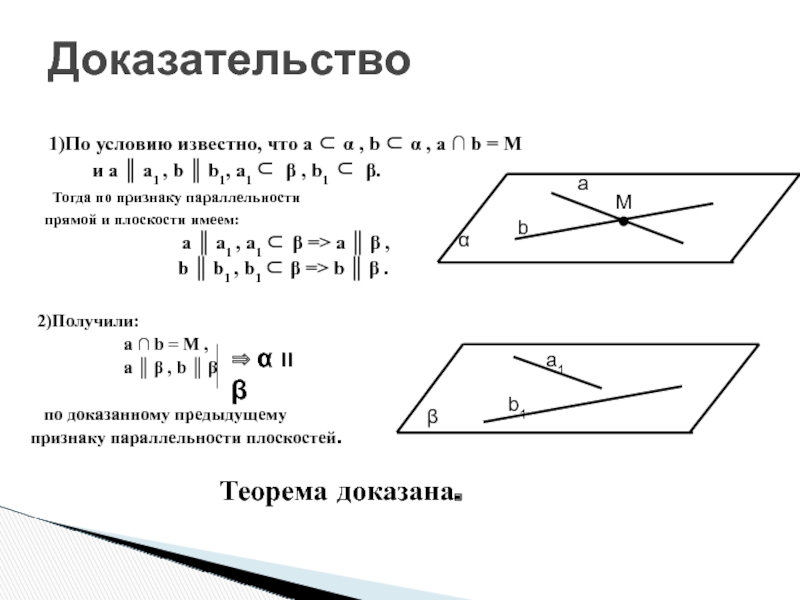
Доказательство
1)По условию известно, что a ⊂ α
, b ⊂ α , a ∩ b = M
и a ║ a1 , b ║ b1, a1 ⊂ β , b1 ⊂ β. Тогда по признаку параллельности
прямой и плоскости имеем:
a ║ a1 , a1 ⊂ β => a ║ β ,
b ║ b1 , b1 ⊂ β => b ║ β .
2)Получили:
a ∩ b = M ,
a ║ β , b ║ β
по доказанному предыдущему
признаку параллельности плоскостей.
Теорема доказана.
М
a
b
α
a1
b1
β
⇒ α װ β
Слайд 78Свойства тетраэдра
Правильный Тетраэдр
Тетра́эдр — многогранник с четырьмя треугольными гранями, в
каждой из вершин которого сходятся по 3 грани. У тетраэдра
4 грани, 4 вершины и 6 рёбер.Параллельные плоскости, проходящие через пары скрещивающихся рёбер тетраэдра, определяют описанный около тетраэдра параллелепипед.
Отрезок, соединяющий вершину тетраэдра с точкой пересечения медиан противоположной грани, называется его медианой, опущенной из данной вершины.
Отрезок, соединяющий середины скрещивающихся рёбер тетраэдра, называется его бимедианой, соединяющей данные рёбра.
Отрезок, соединяющий вершину тетраэдра с точкой противоположной грани и перпендикулярный этой грани, называется его высотой, опущенной из данной вершины.
Теорема. Все медианы и бимедианы тетраэдра пересекаются в одной точке. Эта точка делит медианы в отношении 3:1, считая от вершины. Эта точка делит бимедианы пополам.
Слайд 79Параллелепипед
Свойства
Параллелепипед симметричен относительно середины его диагонали, соединяющей противоположные вершины.
Диагонали параллелепипеда
пересекаются в одной точке и делятся этой точкой пополам.
Противолежащие грани
параллелепипеда параллельны и равны.Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений.
Слайд 81
Геометрические утверждения
Если две точки одной прямой лежат в плоскости, то
и
вся прямая лежит в этой плоскости.
Слайд 82Геометрические утверждения
Если две параллельные плоскости пересечены третьей, то
линии их
пересечения параллельны.
