Различие геометрии Евклида от геометрии Лобачевского.

Орджоникидзе
г. Клинцы Брянская область
Исследовательская работа
Направление: точные науки
Тема:
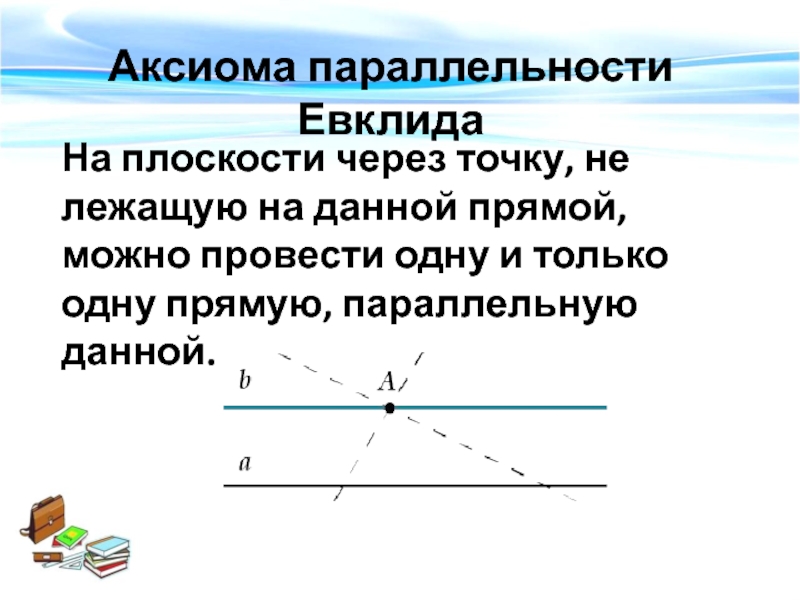
«РАЗЛИЧИЕ ГЕОМЕТРИИ Евклида
и

геометрии Лобачевского»

Выполнил: Сардак Анатолий,
учащийся 10 класса МБОУ-СОШ №3
г. Клинцы

Руководитель: Ломарева Галина Ивановна
учитель математики МБОУ-СОШ №3
г. Клинцы

Клинцы 2018 г.

Евклида и современного ученого Лобачевского.
Задачи:
1. Провести обзор литературы

(книг, научных журналов, форумов) по теме: «Различия Евклидовой геометрии от неевклидовой».
2. Изучить постулаты евклидовой геометрии.
3. Изучить постулаты геометрии Лобачевского.
4. Найти актуальные примеры применения неевклидовой геометрии в современной жизни.
5. Провести опрос «Могут ли пересекаться параллельные прямые? Кто такой Лобачевский? В чем отличия геометрии Лобачевского от геометрии Евклида?»
6. Сформулировать применение постулатов геометрии Лобачевского в современном мире.
7. Сделать выводы об их различии.

Цель и задачи исследования

Казани

прямой, можно провести одну и только одну прямую, параллельную данной.

по крайней мере, две прямые, лежащие с данной прямой в

одной плоскости и не пересекающие её.

геометрии Лобачевского от геометрии Евклида?
Сформулируйте постулат параллельных прямых.

на плоскости.
2. Неевклидова геометрия включает теории Римана и Лобачевского. В

первом случае моделью выступает сфера (например, глобус), параллели на которой пересекаются - меридианы сходятся у полюсов.
Во втором случае теория работает на гиперболическом пространстве, где параллельные прямые не пересекаются.
3. Геометрия Лобачевского нашла применение не только в научных трудах, но и в строительстве, архитектуре, живописи и астрономии.
Работа рассматривает лишь один из аспектов проблемы. Исследования в этом направлении не окончены и будут в дальнейшем продолжены, а результаты будут применены на факультативе по геометрии.