Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Решение неравенств с параметром
Содержание
- 1. Решение неравенств с параметром
- 2. МОУ Огнеупорненская СОШЦель: ознакомить учителей с опытом обучения учащихся решению неравенств с параметром
- 3. МОУ Огнеупорненская СОШплан1. Графики уравнения с двумя
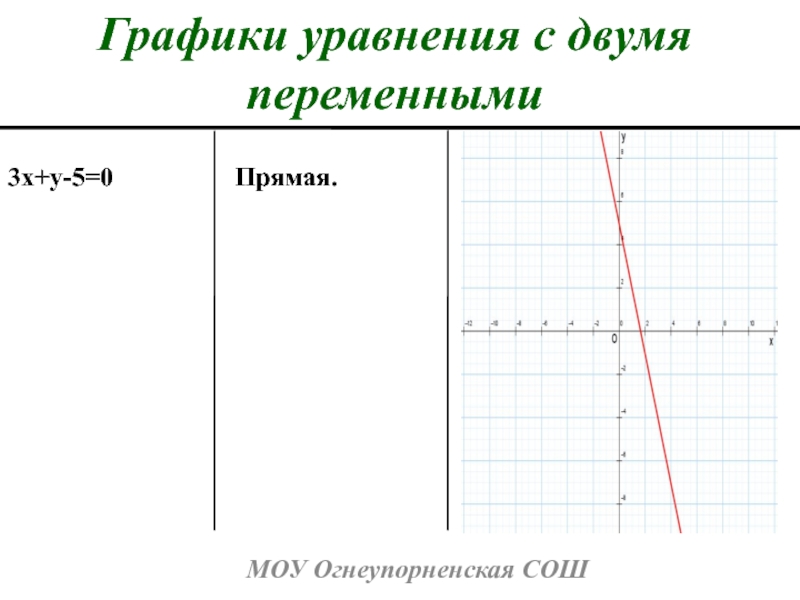
- 4. МОУ Огнеупорненская СОШГрафики уравнения с двумя переменными3x+y-5=0Прямая.
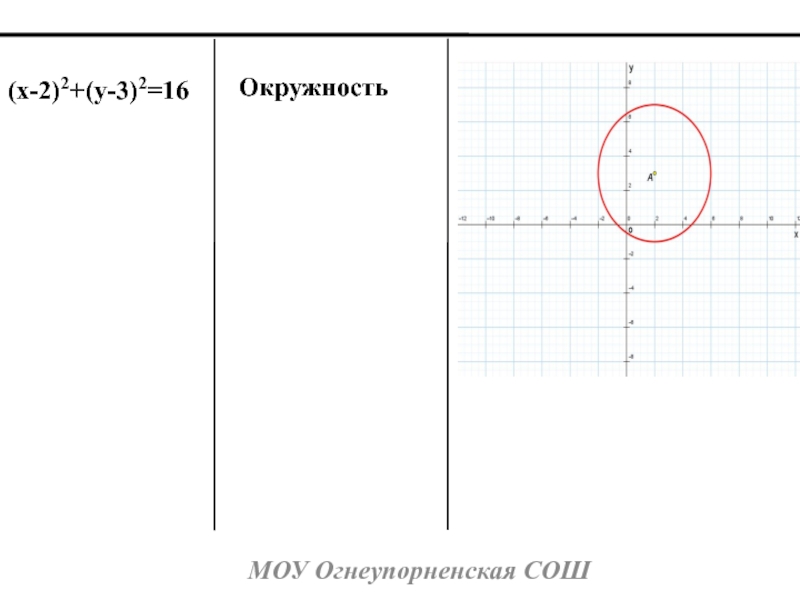
- 5. МОУ Огнеупорненская СОШ(x-2)2+(y-3)2=16Окружность
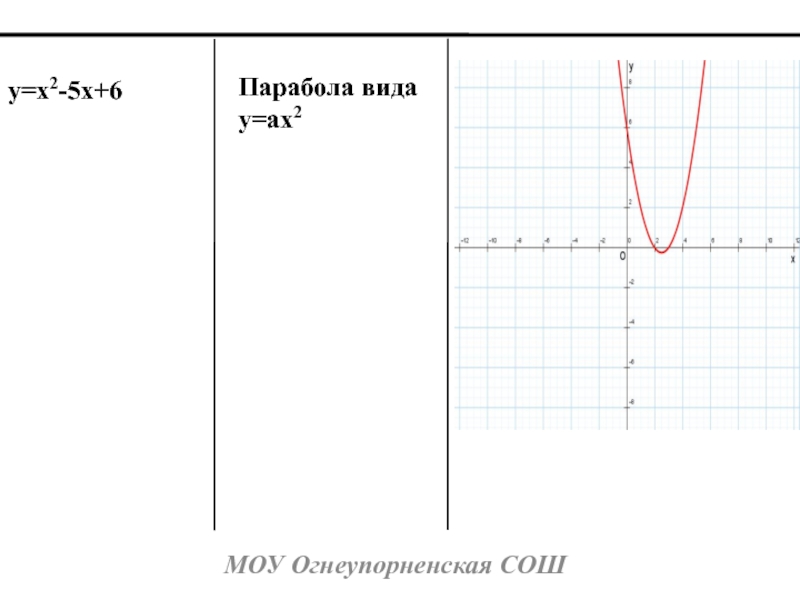
- 6. МОУ Огнеупорненская СОШy=x2-5x+6Парабола видаy=ax2
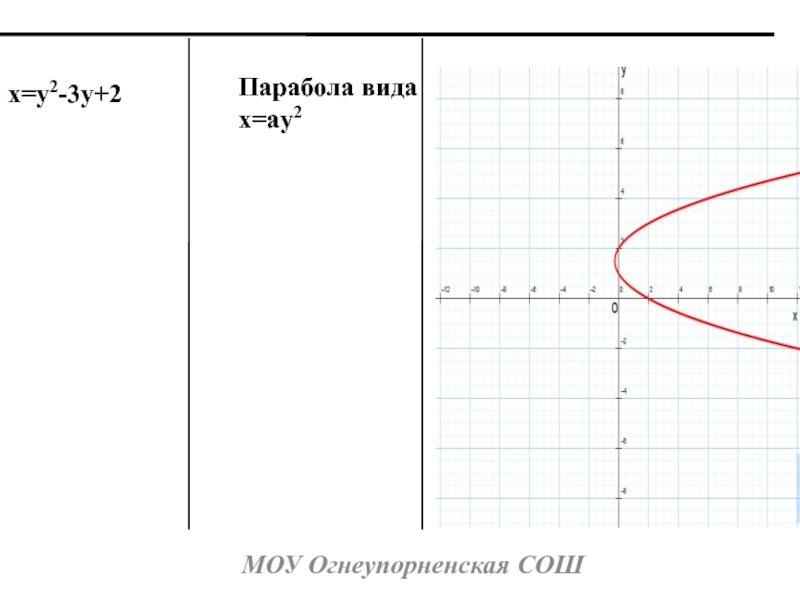
- 7. МОУ Огнеупорненская СОШПарабола видаx=ay2x=y2-3y+2
- 8. МОУ Огнеупорненская СОШГипербола вида(x-2)(y-3)=6
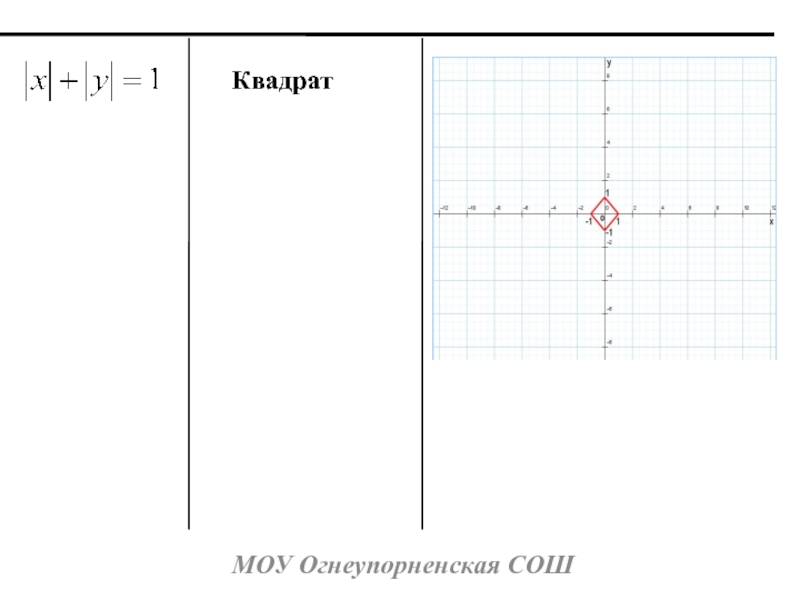
- 9. МОУ Огнеупорненская СОШКвадрат
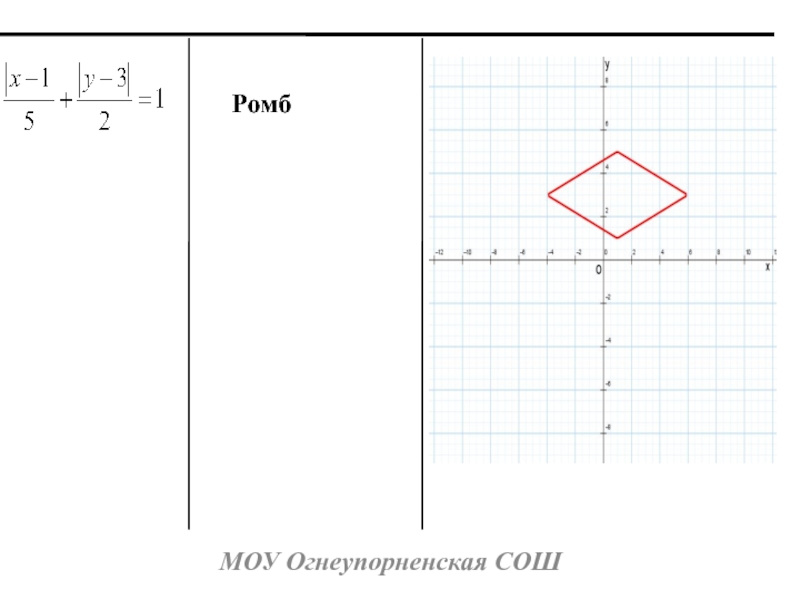
- 10. МОУ Огнеупорненская СОШРомб
- 11. МОУ Огнеупорненская СОШПараллелограмм
- 12. МОУ Огнеупорненская СОШ
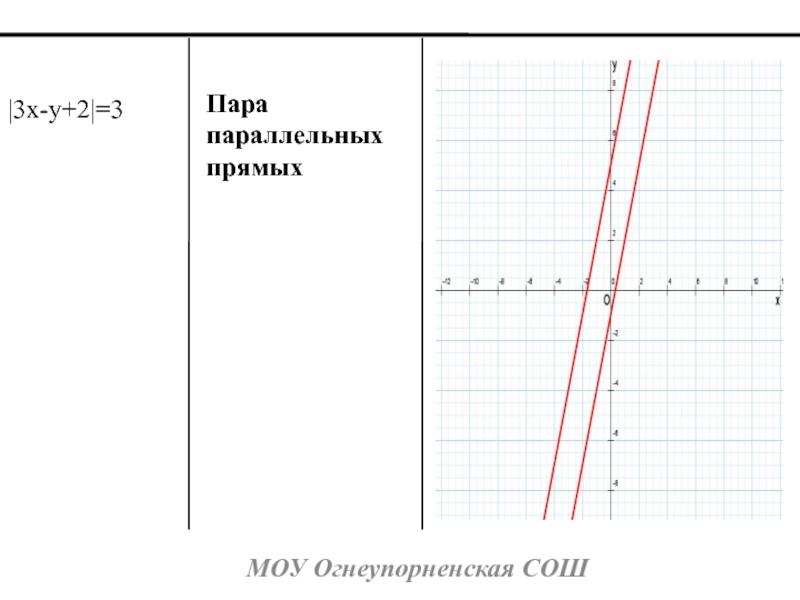
- 13. МОУ Огнеупорненская СОШПара параллельных прямых3x-y+2=3
- 14. Метод областей Пусть F(x;y)=F1(x;y)F2(x;y) …Fn(x;y)
- 15. Обобщенный метод областейПусть
- 16. Решение неравенств с двумяПеременными методом областейПусть дано
- 17. Решить графически неравенство (y+x)(x-y-1)(x+2)0.Решение. F(x;y)=(y+x)(x-y-1)(x+2)2. ОДЗ: xR,
- 18. 2. Решить графически неравенство (y+x-1) 3(2x-3y+8) 20.Решение.
- 19. - 1- 111ху0
- 20. 4.Найти все значения параметра р, при каждом из которыхмножество решений неравенства (p-x2)(p+x-2)
- 21. Рационализация неравенствF(x;y)∨0 G(x;y)∨0 ; a>0, a1; h>0, h1; f>0, g>0МОУ Огнеупорненская СОШ
- 22. МОУ Огнеупорненская СОШУтверждение:u+vh u+vhu-vh
- 23. МОУ Огнеупорненская СОШ5. Найти все значения параметра
- 24. МОУ Огнеупорненская СОШ6. Найти все значения, которые
- 25. МОУ Огнеупорнепрнская СОШ7. Для каждого значения а,
- 26. МОУ Огнеупорненская СОШ7. Записать неравенство, которое задает множество точек плоскости, показанное штриховкой на рисунке.
- 27. Скачать презентанцию
МОУ Огнеупорненская СОШЦель: ознакомить учителей с опытом обучения учащихся решению неравенств с параметром
Слайды и текст этой презентации
Слайд 1Решение неравенств
С параметром
МАСТЕР- КЛАСС
МОУ Огнеупорненская СОШ
Учитель математики абубакиров ж.а.
2011 год
Слайд 2МОУ Огнеупорненская СОШ
Цель: ознакомить учителей с опытом обучения учащихся решению
неравенств с параметром
Слайд 3МОУ Огнеупорненская СОШ
план
1. Графики уравнения с двумя переменными.
2. Метод областей.
3.
Решение неравенств с двумя переменными.
4. Рационализация неравенств.
5. Решение неравенств с
параметрами.6. Творческая лаборатория.
7. Итоги
Слайд 14Метод областей
Пусть F(x;y)=F1(x;y)F2(x;y) …Fn(x;y)
(1)
где Fi(x;y)=pix+qiy+ri, причем прямые pix+qiy+ri=0 и pjx+qjy+rj=0
попарно различны.
Выражению (1)
соответствует разбиение плоскости на области прямыми линиями pix+qiy+ri=0 . Точки пересечения прямых называют особыми точками границы области, другие точки- обыкновенными. Метод областей опирается на следующее свойство чередования знака выражения (1):.
.
При переходе через обыкновенную точку прямой pix+qiy+ri=0 из одной области в смежную знак значения выражения (1) меняется на противоположный
МОУ Огнеупорненская СОШ
Слайд 15Обобщенный метод областей
Пусть
(2)
где Fi(x;y)=pix+qiy+ri, причем прямые pix+qiy+ri=0 и pjx+qjy+rj=0
попарно различны.
Обобщенный метод областей опирается на следующее свойство чередования знака выражения (2):
При переходе через обыкновенную точку прямой pix+qiy+ri=0 из одной области в смежную знак значения выражения (2) меняется на противоположный, если ki – нечетное число, и не меняется, если ki – четное число.
МОУ Огнеупорненская СОШ
Слайд 16Решение неравенств с двумя
Переменными методом
областей
Пусть дано неравенство F(x;y)∨0,где символ
∨ заменяет один из знаков , , , .
Найти ОДЗ.
Построить график уравнения F(x;y)=0.График уравнения разбивает плоскость xOy на области, в каждой из которых выражение F(x;y) сохраняет постоянный знак.
Определить знак выражения F(x;y) в каждой из этих областей.
Записать ответ.
МОУ Огнеупорненская СОШ
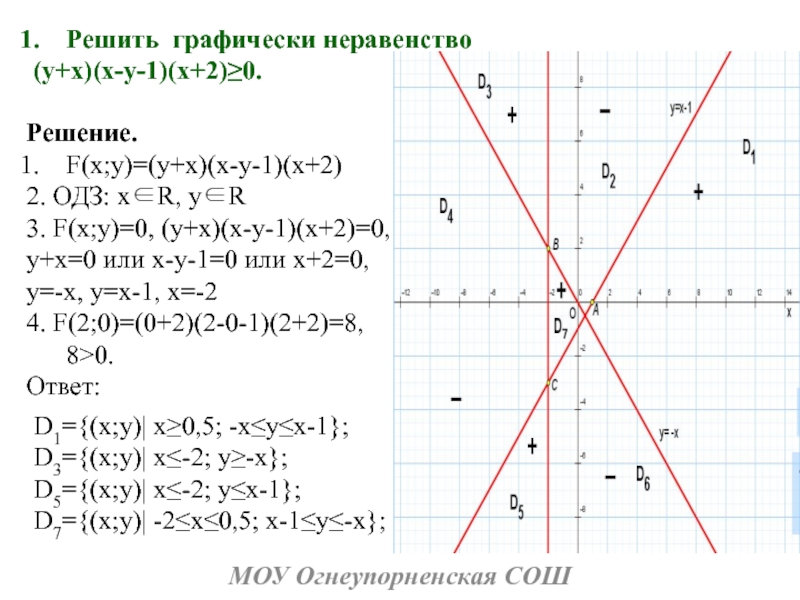
Слайд 17Решить графически неравенство
(y+x)(x-y-1)(x+2)0.
Решение.
F(x;y)=(y+x)(x-y-1)(x+2)
2. ОДЗ: xR, yR
3. F(x;y)=0, (y+x)(x-y-1)(x+2)=0,
y+x=0
или x-y-1=0 или x+2=0,
y=-x, y=x-1, x=-2
4. F(2;0)=(0+2)(2-0-1)(2+2)=8, 8>0.
Ответ:
D1=(x;y) x0,5; -xyx-1;
D3=(x;y)
x-2; y-x;D5=(x;y) x-2; yx-1;
D7=(x;y) -2x0,5; x-1y-x;
МОУ Огнеупорненская СОШ
Слайд 182. Решить графически неравенство
(y+x-1) 3(2x-3y+8) 20.
Решение.
F(x;y)= (y+x-1) 3(2x-3y+8)
2
2. ОДЗ: xR, yR
3. F(x;y)=0, (y+x-1) 3(2x-3y+8) 2 =0,
y+x-1=0 или
2x-3y+8=0 ,y=1-x,
4. F(0;2)= (2+0-1) 3(20-32+8) 2 =4, 4>0.
Ответ:
(x;y) xR, y1-x
МОУ Огнеупорненская СОШ
Слайд 19
- 1
- 1
1
1
х
у
0
3. Решить
графически неравенство
.
1.
2. ОДЗ: x2+y21
3. F(x;y)=0, x2-y2=0, x=y и x2+y2 =1
4. F(0;3)=- 1,125, 1,125>0
D1
D2
D3
D4
D5
D6
D7
D8
МОУ Огнеупорненская СОШ
Ответ: D1=(x;y) x2+y2 >1;-yxy;
D7=(x;y) x2+y2 <1;-1
D5=(x;y) x2+y2 <1;0x<1; -xyx;
Слайд 204.Найти все значения параметра р, при каждом из которых
множество решений
неравенства (p-x2)(p+x-2)
F(x;p)=(p-x2)(p+x-2)
Из полученного множества
исключим решения неравенства
x21. Получим p0, p3.
Ответ: p0, p3.
2. F(x;p)=0, (p-x2)(p+x-2)=0,
p= x2 или p=-x+2
р = 3
р = 0
0
2
2
-1
1
3
1
-
+
-
+
3. F(3;1)=(1-9)(1+3-2)=-16, -16<0
-
D1
D2
D3
D4
D5
Решение.
МОУ Огнеупорненская СОШ
Слайд 21 Рационализация неравенств
F(x;y)∨0 G(x;y)∨0 ; a>0, a1; h>0, h1;
f>0, g>0
МОУ Огнеупорненская СОШ
Слайд 23МОУ Огнеупорненская СОШ
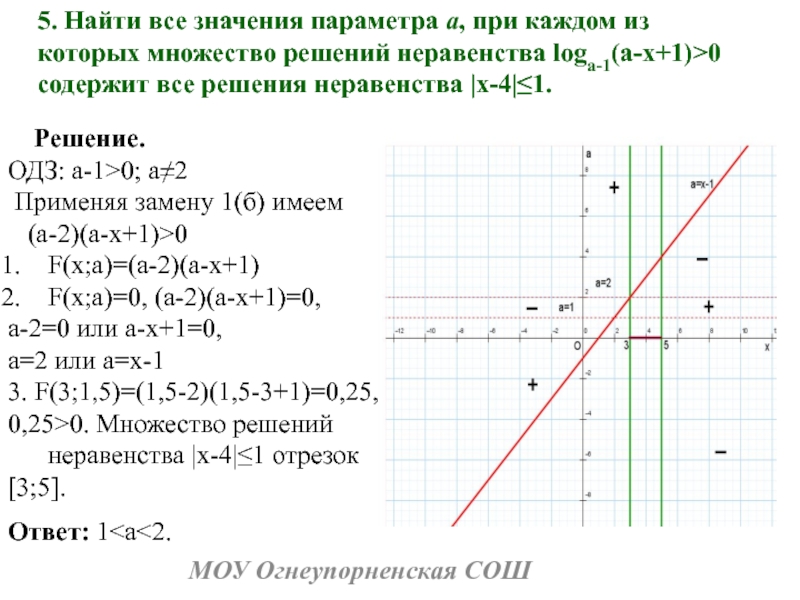
5. Найти все значения параметра a, при каждом
из которых множество решений неравенства loga-1(a-x+1)>0 содержит все решения неравенства
x-41.Решение.
ОДЗ: a-1>0; a2
Применяя замену 1(б) имеем
(a-2)(a-x+1)>0
F(x;a)=(a-2)(a-x+1)
F(x;a)=0, (a-2)(a-x+1)=0,
a-2=0 или a-x+1=0,
a=2 или a=x-1
3. F(3;1,5)=(1,5-2)(1,5-3+1)=0,25,
0,25>0. Множество решений неравенства x-41 отрезок
3;5.
Ответ: 1
Слайд 24МОУ Огнеупорненская СОШ
6. Найти все значения, которые может принимать сумма
x+a при условии 2x+4-2a+x-2+a3.
Решение.
2x+4-2a+x-2+a3
3x-a+23
x-3a+63
3x-a+2=3, 3x-a+2=3 или
3x-a+2=-3, a=3x-1
или a=3x+52. x-3a+6=3, x-3a+6=3 или
x-3a+6=-3, или
Наибольшее значение x+a равно 1,5+3,5=5.
Наименьшее значение x+a равно -1,5+0,5=-1.
Ответ: -1;5
Слайд 25МОУ Огнеупорнепрнская СОШ
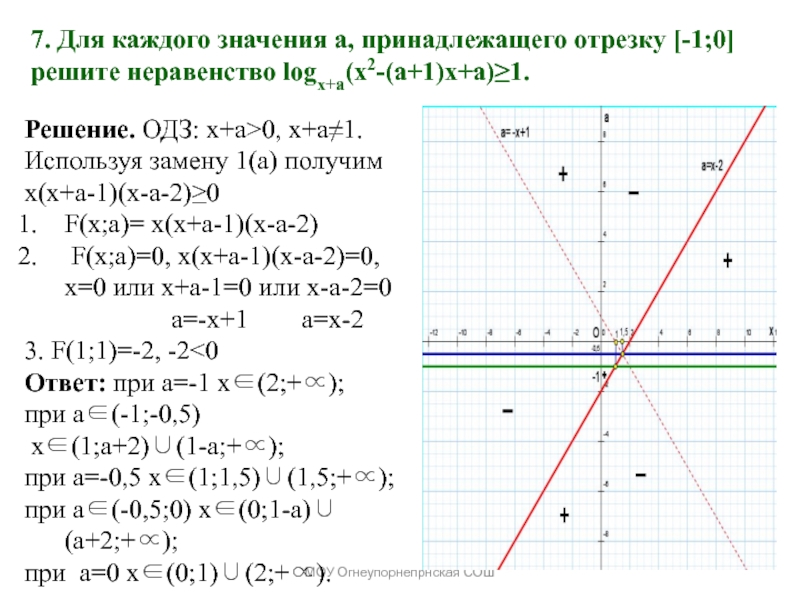
7. Для каждого значения а, принадлежащего отрезку -1;0
решите неравенство logx+a(x2-(a+1)x+a)1.
Решение. ОДЗ: x+a>0, x+a1.
Используя замену 1(а) получим x(x+a-1)(x-a-2)0
F(x;a)=
x(x+a-1)(x-a-2)F(x;a)=0, x(x+a-1)(x-a-2)=0, x=0 или x+a-1=0 или x-a-2=0
a=-x+1 a=x-2
3. F(1;1)=-2, -2<0
Ответ: при а=-1 x(2;+);
при а(-1;-0,5)
x(1;a+2)(1-a;+);
при а=-0,5 x(1;1,5)(1,5;+);
при а(-0,5;0) x(0;1-a)(а+2;+);
при а=0 x(0;1)(2;+).
Слайд 26МОУ Огнеупорненская СОШ
7. Записать неравенство, которое задает множество точек плоскости,
показанное штриховкой на рисунке.
