Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Функции и их графики на ОГЭ
Содержание
- 1. Функции и их графики на ОГЭ
- 2. Обобщить и систематизировать знания, умения, навыки по
- 3. 1. График какой функции изображён на рисунке:y=2x+4y=-2x+4y=x²-4y=-x²+4420
- 4. 2. Какая из следующих парабол отсутствует на рисунке?y=(x-2)² y=(x+2)²y=x²+2y=x²-2
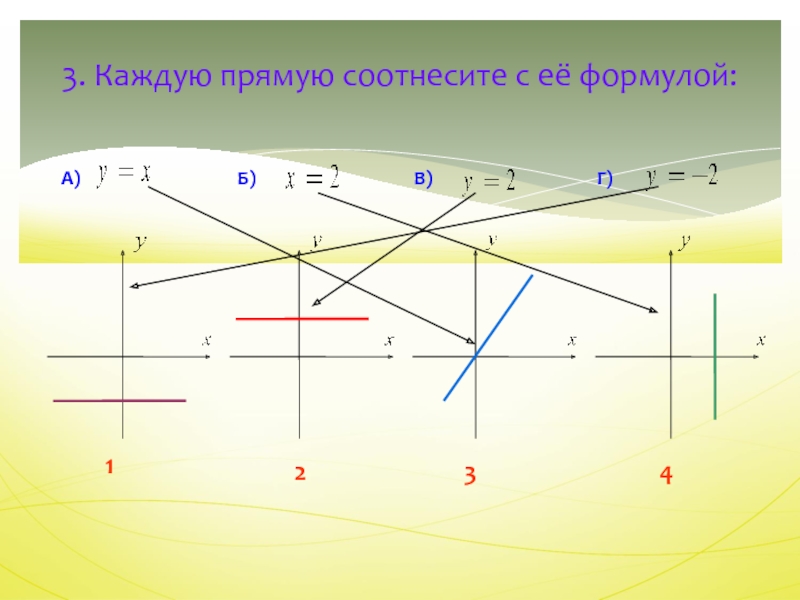
- 5. 3. Каждую прямую соотнесите с её формулой:А)Б)В)Г)1234
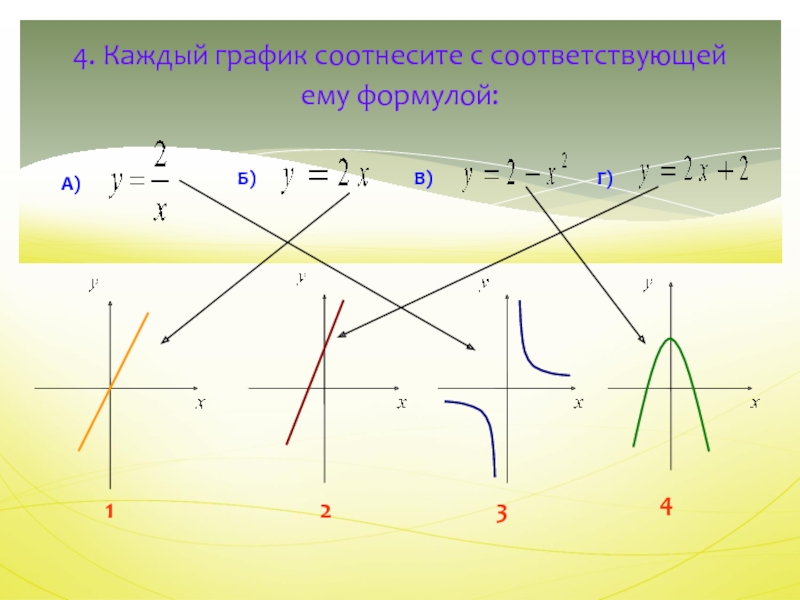
- 6. 4. Каждый график соотнесите с соответствующей ему формулой: А)Б)В)Г)1234
- 7. 5. Используя график функции y=f(x), определите, какое утверждение верно:f(-1)
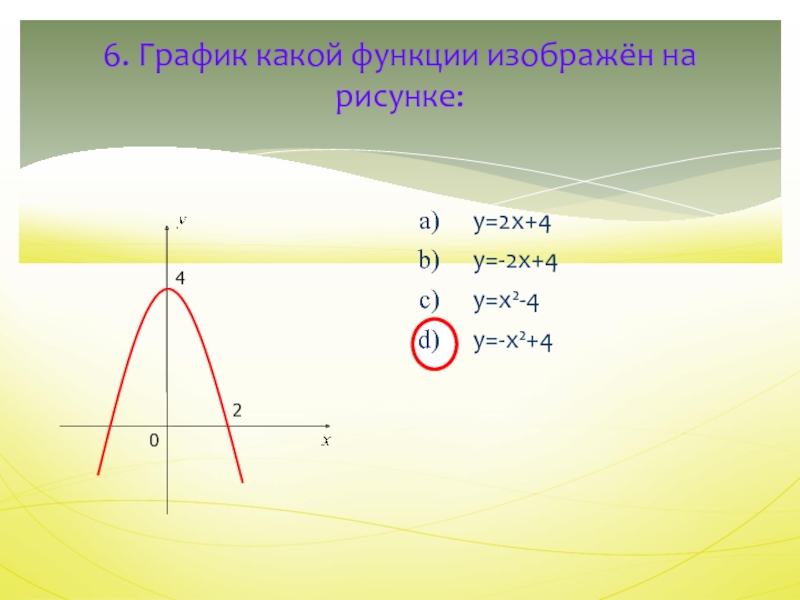
- 8. 6. График какой функции изображён на рисунке:y=2x+4y=-2x+4y=x²-4y=-x²+4420
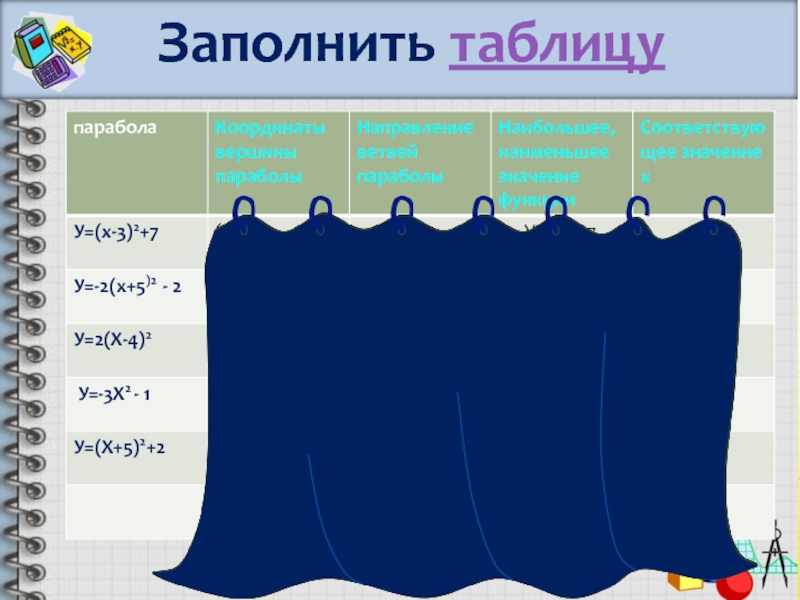
- 9. Заполнить таблицу
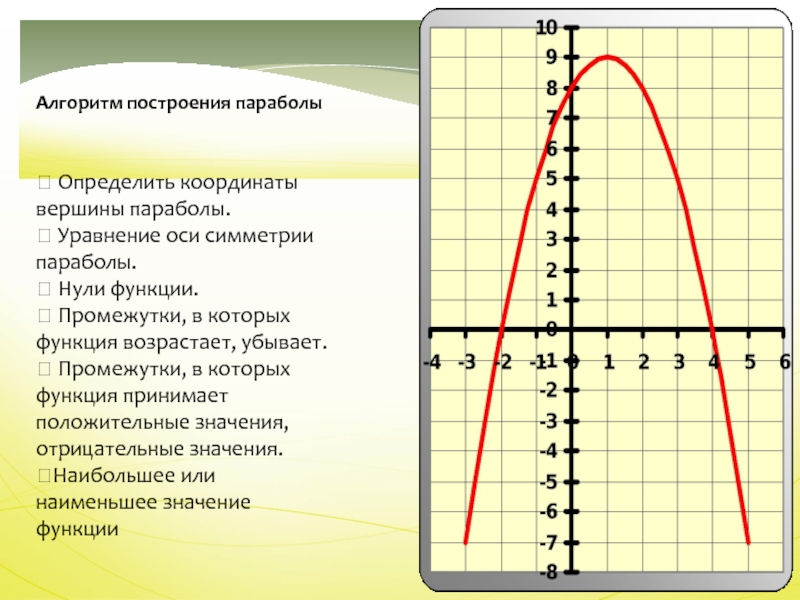
- 10. Алгоритм построения параболы⮚ Определить координаты вершины параболы.⮚
- 11. Вершина параболы:
- 12. С Ох: у=0
- 13. УУУУстановите соответствие:
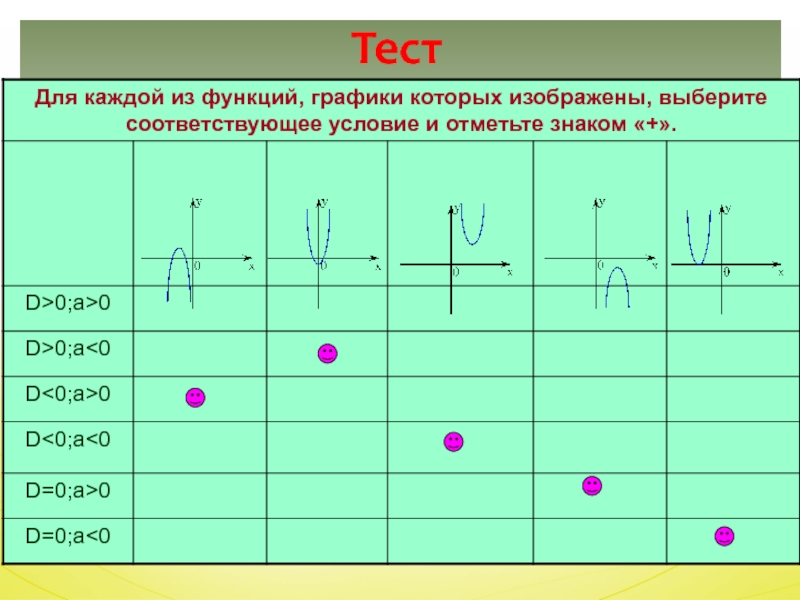
- 14. Найти знаки a и D
- 15. Тест
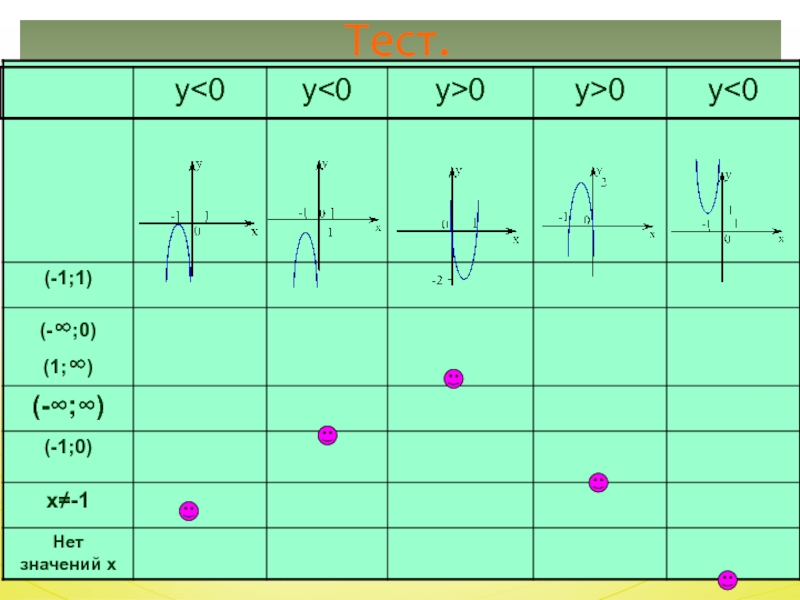
- 16. Тест.
- 17. У = -х2-6х-8Построить график функции и по графику выяснить ее свойства.Свойства функции:у>0 на промежуткеу
- 18. План построенияyx1) Построить вершину параболы -7-12) Построить
- 19. Задание 1
- 20. Задание 2 На
- 21. Задание 3 На
- 22. Задание 4 На каком рисунке изображён
- 23. у= 2х22134Параболу, построенную в координатной плоскости, соотнесите с ее уравнением у= –х2у= х2у= х2 – 1ПОДУМАЙ!ВЕРНО!ПОДУМАЙ!ПОДУМАЙ!
- 24. 1 2 3 4
- 25. 1 2 3 4
- 26. ВЕРНО!у=3х2+4х+14213Какая из функций является ограниченной сверху? у=(–х–2)2+1у=(х+2)2–1у=–(х+2)2–1ПОДУМАЙ!ПОДУМАЙ!ПОДУМАЙ!
- 27. ВЕРНО!1243Какая из функций является ограниченной снизу? у=(–х–1)2+2у=–2х2+1у=–2(х–1)2–2ПОДУМАЙ!ПОДУМАЙ!ПОДУМАЙ!у=–(х–1)2+2у=(–х–1)2 +2=(–(х+1))2 +2 = (х+1)2 +2 a > 0
- 28. у = х2 – 7х +
- 29. у = х2 – 7х +
- 30. 134По графику функции найдите промежутки ее возрастания.
- 31. Выберите график, соответствующий функции у = (х – 1)2 – 1342ПОДУМАЙ!ПОДУМАЙ!00хуухххуу001-111-1-1-111Верно! ПОДУМАЙ!
- 32. 134Какую из функций можно назвать обратной пропорциональностью? ПОДУМАЙ!ВЕРНО!ПОДУМАЙ!ПОДУМАЙ!2
- 33. прямая, проходящая через II и IV координатные четвертиКакая линия является графиком функции3214прямая, проходящая через начало координатПОДУМАЙ!ПОДУМАЙ!ПОДУМАЙ!гиперболапараболаВЕРНО!
- 34. График какой из приведенных ниже функций изображен на рисунке?
- 35. Какой из графиков функций, представленных на рисунке является гиперболой?342ПОДУМАЙ!ПОДУМАЙ!00хуухххуу001-111-1-1-111гипербола ПОДУМАЙ!
- 36. Нахождение значения коэффициента а по графику квадратичной
- 37. Найдите значение а по графику функции
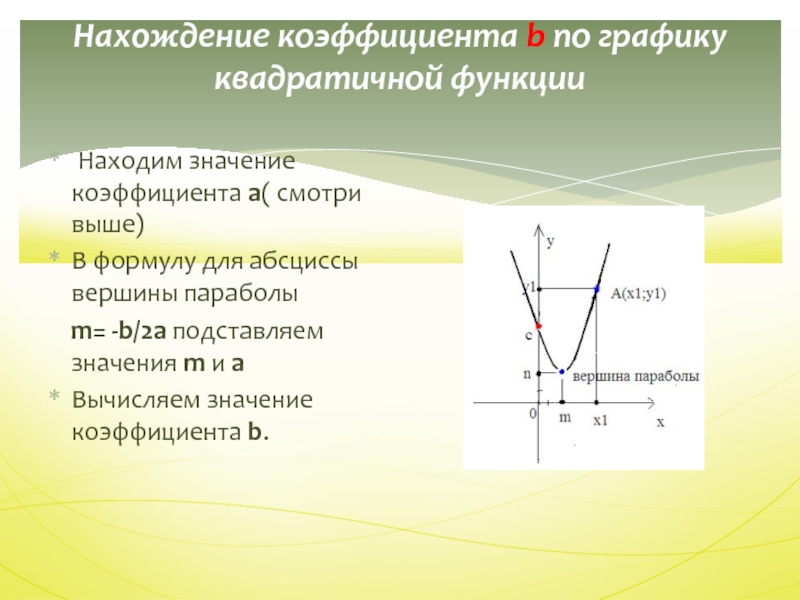
- 38. Нахождение коэффициента b по графику квадратичной функции
- 39. Найдите значение b по графику функции
- 40. Нахождение коэффициента с по графику квадратичной
- 41. Найдите значение с по графику функции
- 42. Найдите значение коэффициентов а,b,с по графику функции
- 43. Найдите значение а по графику функции у
- 44. Найдите значение b по графику функции у
- 45. Найдите значение c по графику функции у
- 46. Список литературы:1. "Алгебра. Учебник для 8 кл. общеобразовательных учреждений" Ю.Н. Макарычев
- 47. Скачать презентанцию
Обобщить и систематизировать знания, умения, навыки по теме урокаПродолжить работу по подготовке к ОГЭРазвивать логическое мышление, речь, память, вниманиеВоспитывать аккуратность, самостоятельностьЦели урока:
Слайды и текст этой презентации
Слайд 2Обобщить и систематизировать знания, умения, навыки по теме урока
Продолжить работу
по подготовке к ОГЭ
Развивать логическое мышление, речь, память, внимание
Воспитывать аккуратность,
самостоятельностьЦели урока:
Слайд 7
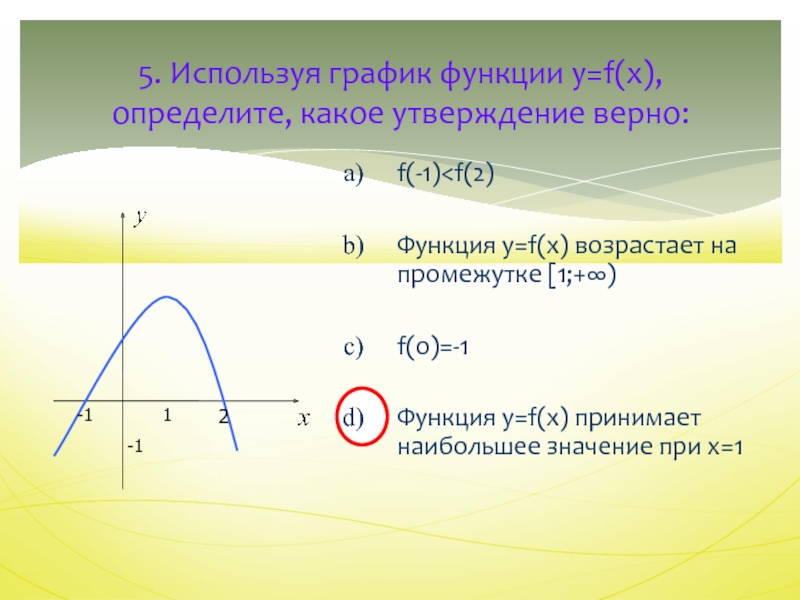
5. Используя график функции y=f(x), определите, какое утверждение верно:
f(-1)
возрастает на промежутке [1;+∞)
f(0)=-1
Функция y=f(x) принимает наибольшее значение при x=1
-1
1
2
-1
Слайд 10
Алгоритм построения параболы
⮚ Определить координаты
вершины параболы.
⮚ Уравнение оси симметрии
параболы.
⮚ Нули функции.
⮚ Промежутки, в которых функция возрастает, убывает.
⮚ Промежутки,
в которых функция принимает положительные значения, отрицательные значения.⮚Наибольшее или наименьшее значение функции
Слайд 11Вершина параболы:
Задание.
Найти
координаты вершины параболы:
1) у = х 2 -4х-5 2) у=-5х 2+3Ответ:(2;-9) Ответ:(0;3)
Уравнение оси симметрии: х=х0
Слайд 12С Ох: у=0 ах2+bх+с=0
С Оу: х=0
у=с
Задание.
Найти координаты точек пересечения параболы с
осями координат:1)у=х2-х; 2)у=х2+3; 3)у=5х2-3х-2
(0;0);(1;0) (0;3) (1;0);(-0,4;0);(0;2)
Координаты точек пересечения параболы с осями координат.
Слайд 17У = -х2-6х-8
Построить график функции и по графику выяснить ее
свойства.
Свойства функции:
у>0 на промежутке
у
на промежуткеНаибольшее значение функции равно
(-4;-2)
(-∞;-4)U(-2;∞)
(-∞;-3]
[-3;∞)
1, при х=-3
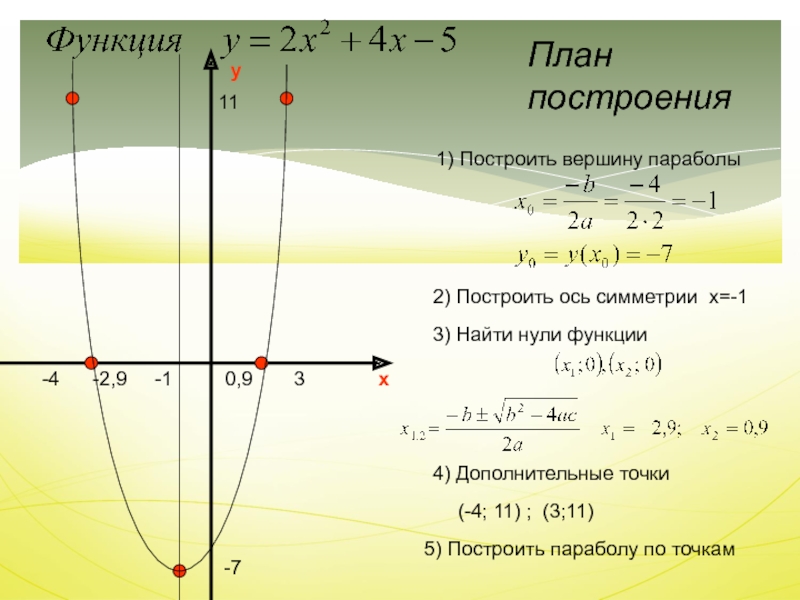
Слайд 18
План построения
y
x
1) Построить вершину параболы
-7
-1
2) Построить ось симметрии x=-1
3)
Найти нули функции
-2,9
0,9
4) Дополнительные точки
11
-4
3
(-4; 11) ; (3;11)
5) Построить параболу по точкам
Слайд 19Задание 1
На рисунке изображен
график квадратичной функции. Какая из перечисленных формул задает эту функцию?
Слайд 20Задание 2
На рисунке изображен график
квадратичной функции. Какая из перечисленных формул задает эту функцию?
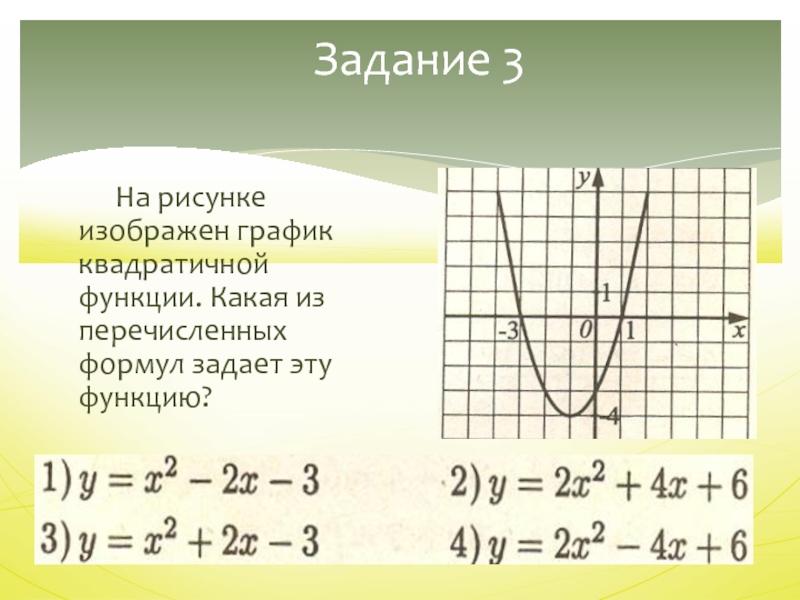
Слайд 21Задание 3
На рисунке изображен график
квадратичной функции. Какая из перечисленных формул задает эту функцию?
Слайд 22Задание 4
На каком рисунке изображён график функции y=f(x),
обладающий свойствами:f(0)=2 и функция убывает на промежутке
(- ; 1]?
Слайд 23у= 2х2
2
1
3
4
Параболу, построенную в координатной плоскости, соотнесите с ее уравнением
у= –х2
у= х2
у= х2 – 1
ПОДУМАЙ!
ВЕРНО!
ПОДУМАЙ!
ПОДУМАЙ!
Слайд 24
1 2 3 4 5 6
7
-7 -6 -5 -4 -3 -2 -1
7
6
5
4
3
2
1
-1
-2
-3
-4
-5
-6
-7
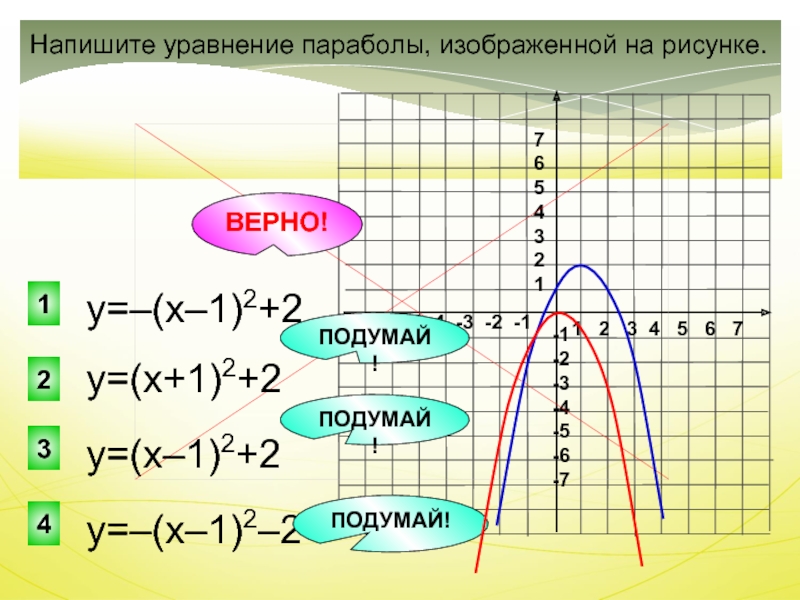
у=(х+1)2+2
1
2
3
4
ВЕРНО!
Напишите уравнение параболы,
изображенной на рисунке. у=–(х–1)2+2
у=(х–1)2+2
у=–(х–1)2–2
ПОДУМАЙ!
ПОДУМАЙ!
ПОДУМАЙ!
Слайд 25
1 2 3 4 5 6
7
-7 -6 -5 -4 -3 -2 -1
7
6
5
4
3
2
1
-1
-2
-3
-4
-5
-6
-7
1
3
2
1
4
ВЕРНО!
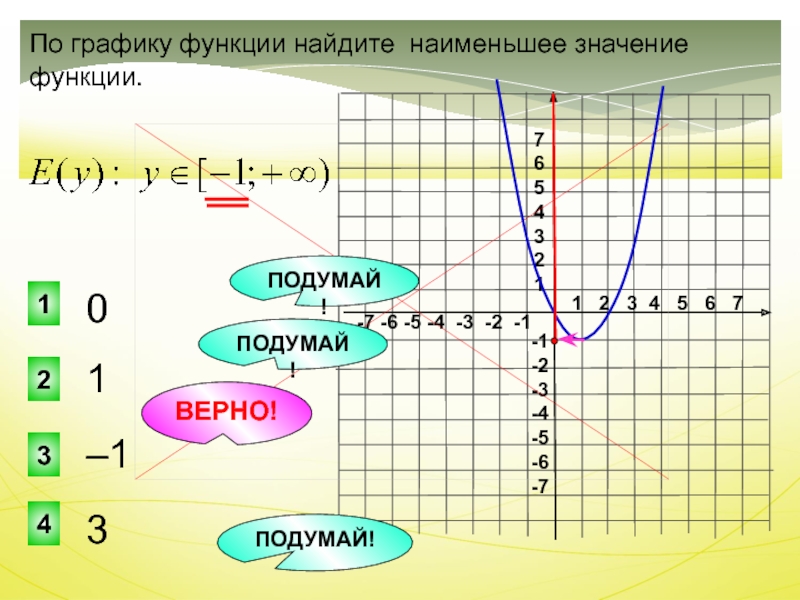
По графику функции
найдите наименьшее значение функции. 0
–1
3
ПОДУМАЙ!
ПОДУМАЙ!
ПОДУМАЙ!
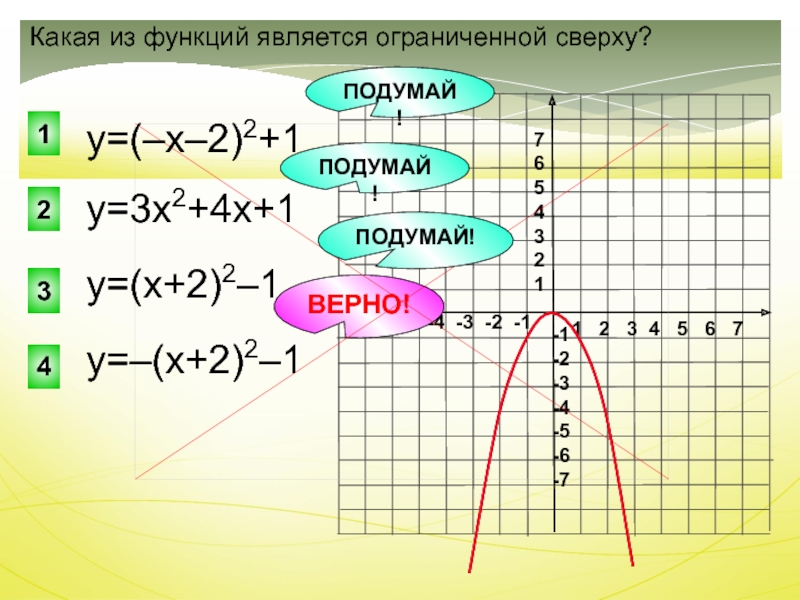
Слайд 26ВЕРНО!
у=3х2+4х+1
4
2
1
3
Какая из функций является ограниченной сверху?
у=(–х–2)2+1
у=(х+2)2–1
у=–(х+2)2–1
ПОДУМАЙ!
ПОДУМАЙ!
ПОДУМАЙ!
Слайд 27ВЕРНО!
1
2
4
3
Какая из функций является ограниченной снизу?
у=(–х–1)2+2
у=–2х2+1
у=–2(х–1)2–2
ПОДУМАЙ!
ПОДУМАЙ!
ПОДУМАЙ!
у=–(х–1)2+2
у=(–х–1)2 +2
=(–(х+1))2 +2
=
(х+1)2 +2
a > 0
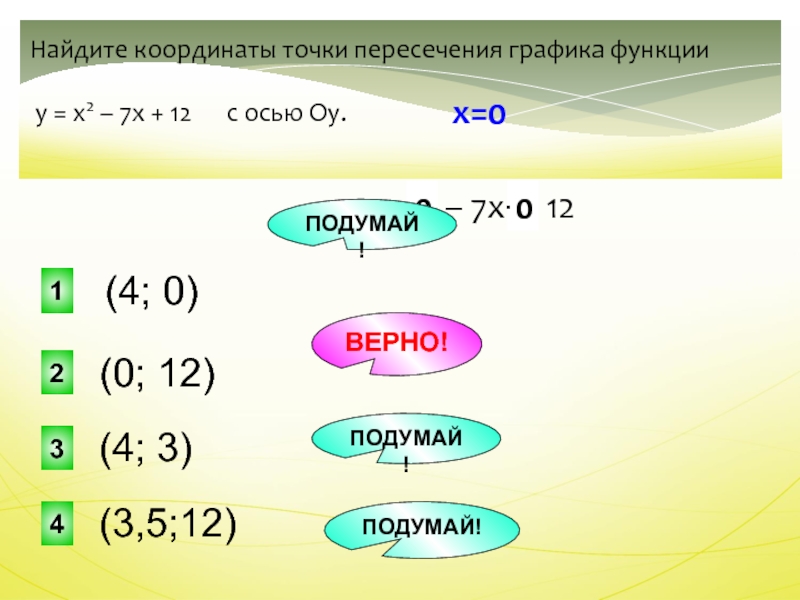
Слайд 28 у = х2 – 7х + 12
(0; 12)
Найдите координаты
точки пересечения графика функции
у = х2 – 7х +
12 с осью Оу.0
2
1
3
4
(4; 0)
(4; 3)
(3,5;12)
ПОДУМАЙ!
ВЕРНО!
ПОДУМАЙ!
ПОДУМАЙ!
х=0
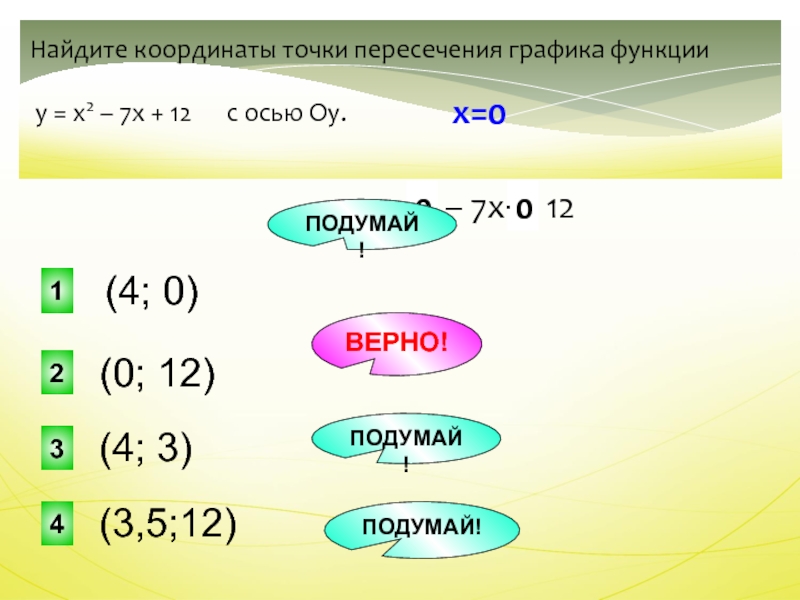
Слайд 29 у = х2 – 7х + 12
(0; 12)
Найдите координаты
точки пересечения графика функции
у = х2 – 7х +
12 с осью Оу.0
2
1
3
4
(4; 0)
(4; 3)
(3,5;12)
ПОДУМАЙ!
ВЕРНО!
ПОДУМАЙ!
ПОДУМАЙ!
х=0
Слайд 301
3
4
По графику функции найдите промежутки ее возрастания.
1 2
3 4 5 6 7
-7 -6
-5 -4 -3 -2 -17
6
5
4
3
2
1
-1
-2
-3
-4
ПОДУМАЙ!
ВЕРНО!
ПОДУМАЙ!
ПОДУМАЙ!
2
(– ;–1]
8
[–3; 1]
Слайд 31Выберите график, соответствующий функции
у = (х – 1)2 –
1
3
4
2
ПОДУМАЙ!
ПОДУМАЙ!
0
0
х
у
у
х
х
х
у
у
0
0
1
-1
1
1
-1
-1
-1
1
1
Верно!
ПОДУМАЙ!
Слайд 321
3
4
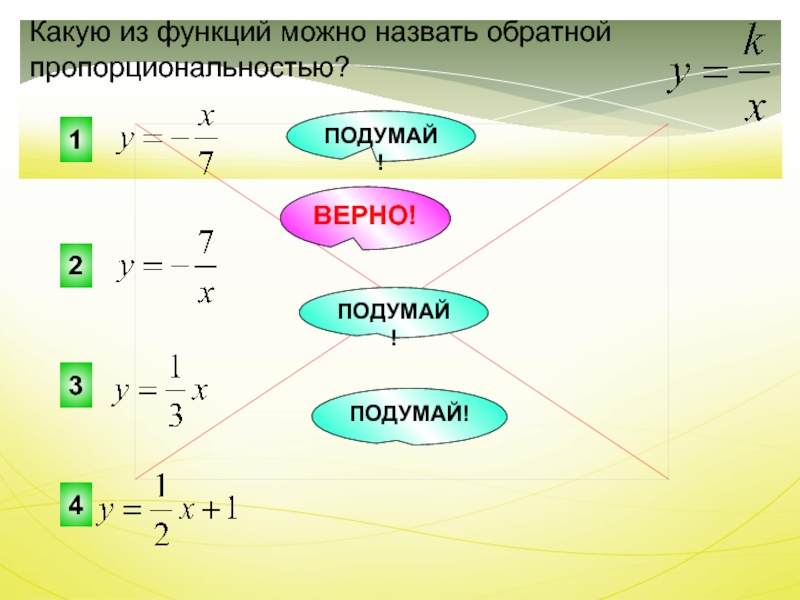
Какую из функций можно назвать обратной пропорциональностью?
ПОДУМАЙ!
ВЕРНО!
ПОДУМАЙ!
ПОДУМАЙ!
2
Слайд 33
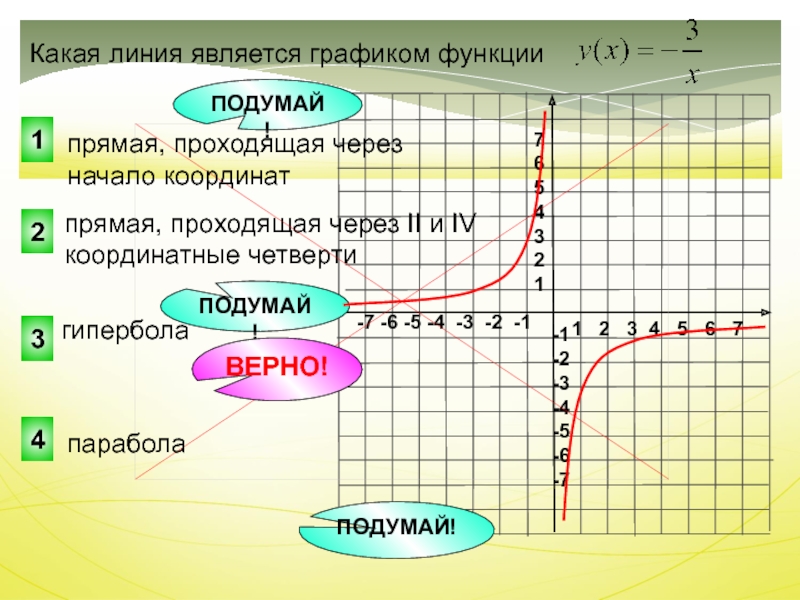
прямая, проходящая через II и IV координатные четверти
Какая линия является
графиком функции
3
2
1
4
прямая, проходящая через начало координат
ПОДУМАЙ!
ПОДУМАЙ!
ПОДУМАЙ!
гипербола
парабола
ВЕРНО!
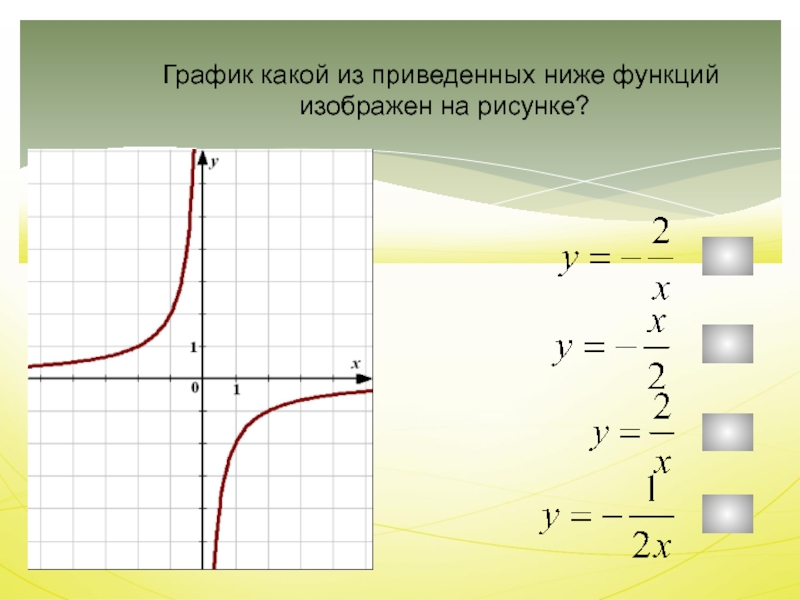
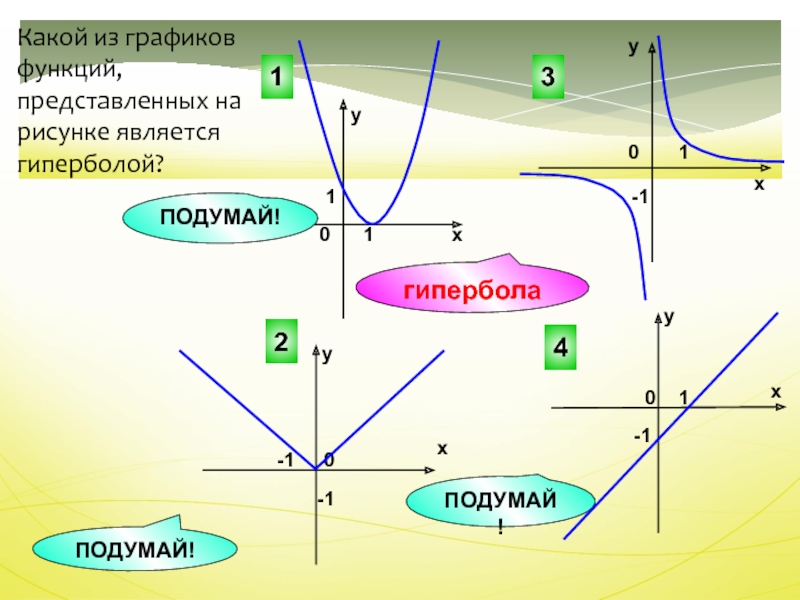
Слайд 35Какой из графиков функций, представленных на рисунке является гиперболой?
3
4
2
ПОДУМАЙ!
ПОДУМАЙ!
0
0
х
у
у
х
х
х
у
у
0
0
1
-1
1
1
-1
-1
-1
1
1
гипербола
ПОДУМАЙ!
Слайд 36Нахождение значения коэффициента а по графику квадратичной функции
1) по
графику определяем координаты вершины (m,n)
2) по графику определяем
координаты любой точки А (х1;у1)3) подставляем эти значения в формулу квадратичной функции, заданной в виде:
У=a(х-m)2+n
4) решаем полученное уравнение.
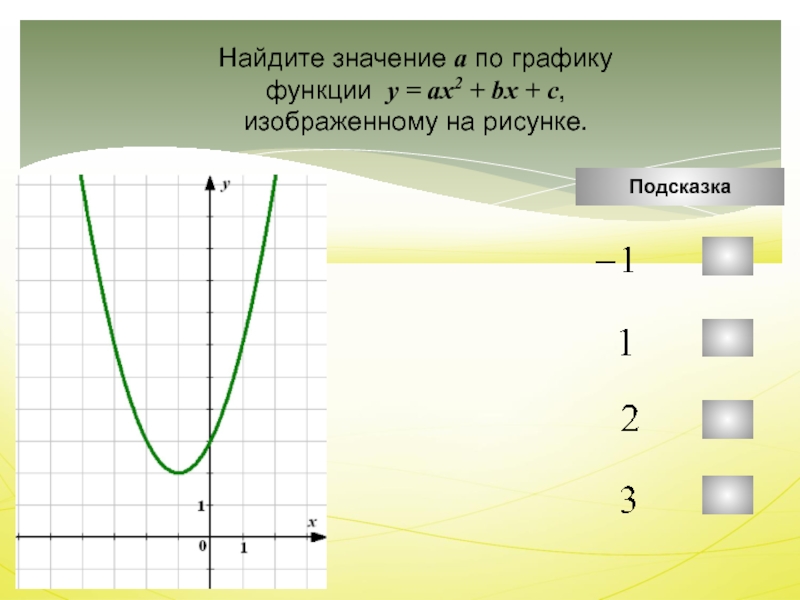
Слайд 37
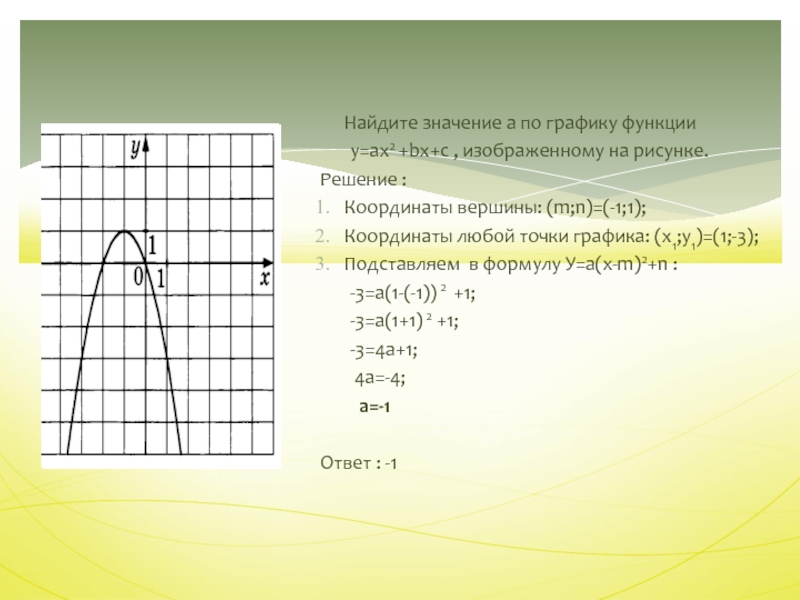
Найдите значение а по графику функции
у=ax2
+bx+c , изображенному на рисунке.
Решение :
Координаты вершины: (m;n)=(-1;1);
Координаты любой точки
графика: (х1;у1)=(1;-3);Подставляем в формулу У=a(х-m)2+n :
-3=а(1-(-1)) 2 +1;
-3=а(1+1) 2 +1;
-3=4а+1;
4а=-4;
а=-1
Ответ : -1
Слайд 38Нахождение коэффициента b по графику квадратичной функции
Находим значение коэффициента
a( смотри выше)
В формулу для абсциссы вершины параболы
m=
-b/2a подставляем значения m и a Вычисляем значение коэффициента b.
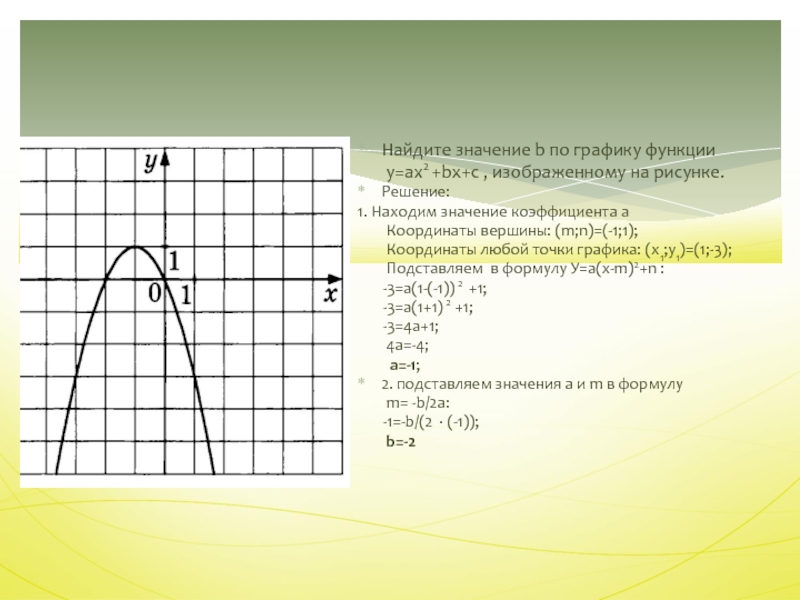
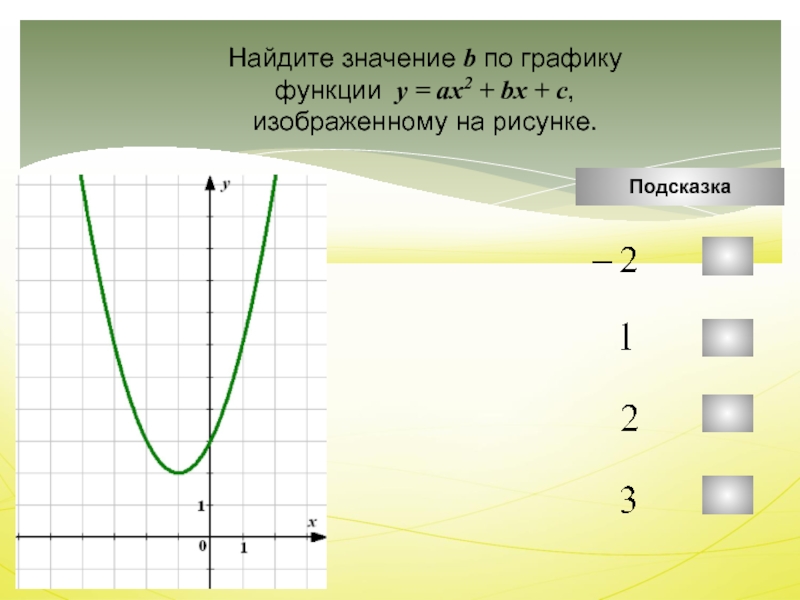
Слайд 39
Найдите значение b по графику функции
у=ax2
+bx+c , изображенному на рисунке.
Решение:
1. Находим значение коэффициента а
Координаты вершины: (m;n)=(-1;1);Координаты любой точки графика: (х1;у1)=(1;-3);
Подставляем в формулу У=a(х-m)2+n :
-3=а(1-(-1)) 2 +1;
-3=а(1+1) 2 +1;
-3=4а+1;
4а=-4;
а=-1;
2. подставляем значения а и m в формулу
m= -b/2a:
-1=-b/(2 · (-1));
b=-2
Слайд 40 Нахождение коэффициента с по графику квадратичной функции
Находим ординату точки
пересечения графика с осью Оу, это значение равно коэффициенту с,
т.е. точка (0;с)-точка пересечения параболы с осью Оу.Если по графику невозможно найти точку пересечения с осью Оу, то находим коэффициенты a;b
Подставляем найденные значения a, b , координаты А(х1 ;у1) в уравнение
у=ax2 +bx+c и находим с.
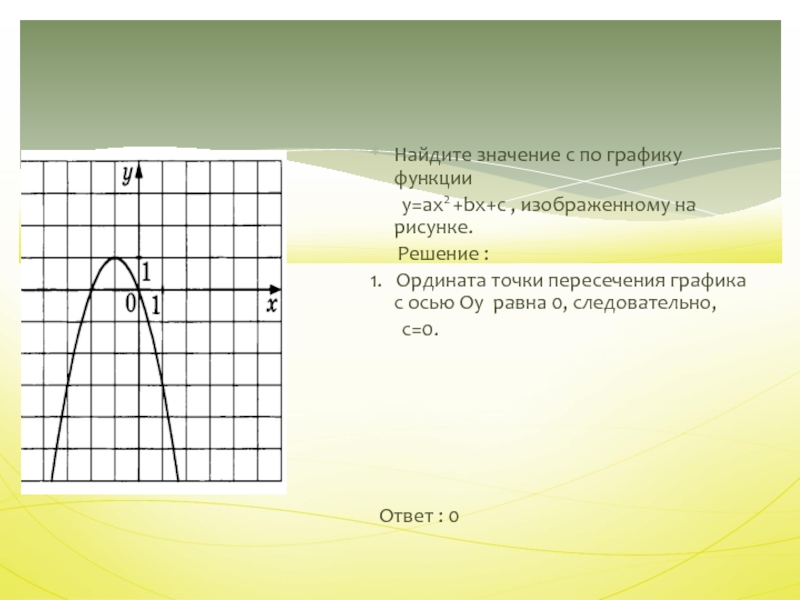
Слайд 41
Найдите значение с по графику функции
у=ax2
+bx+c , изображенному на рисунке.
Решение :
1.
Ордината точки пересечения графика с осью Оу равна 0, следовательно, с=0.
Ответ : 0
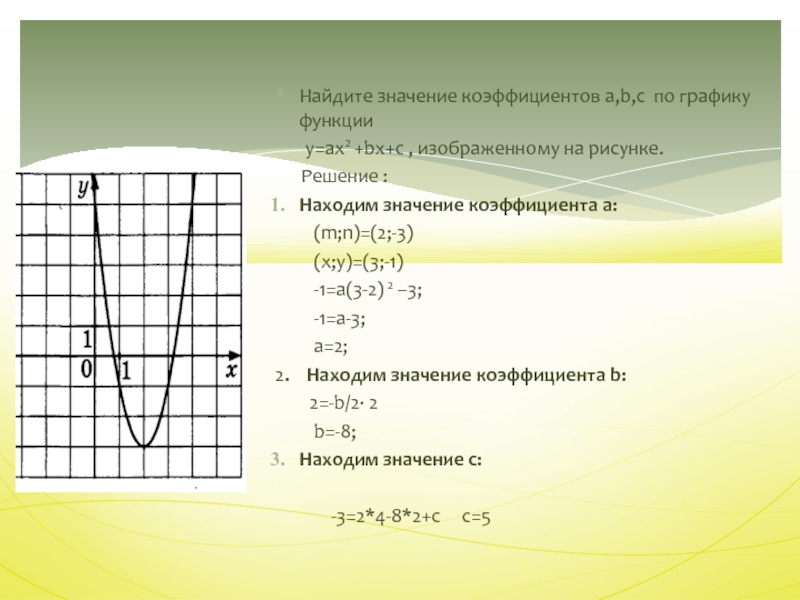
Слайд 42
Найдите значение коэффициентов а,b,с по графику функции
у=ax2 +bx+c , изображенному на рисунке.
Решение :
Находим
значение коэффициента а:(m;n)=(2;-3)
(х;у)=(3;-1)
-1=а(3-2) 2 –3;
-1=а-3;
а=2;
2. Находим значение коэффициента b:
2=-b/2· 2
b=-8;
Находим значение с:
-3=2*4-8*2+с с=5
Слайд 46Список литературы:
1. "Алгебра. Учебник для 8 кл. общеобразовательных учреждений" Ю.Н. Макарычев и др., изд-во
«Просвещение», 2014.;
2. "Алгебра. Учебник для 9 кл. общеобразовательных учреждений" Ю.Н. Макарычев и др., изд-во
«Просвещение», 2011.;3. ОГЭ, Математика, 3000 задач с ответами, Часть 1, 2014.Семенов А.Л., Ященко И.В., 2013.
