Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Решение неравенств второй степени с одной переменной
Содержание
- 1. Решение неравенств второй степени с одной переменной
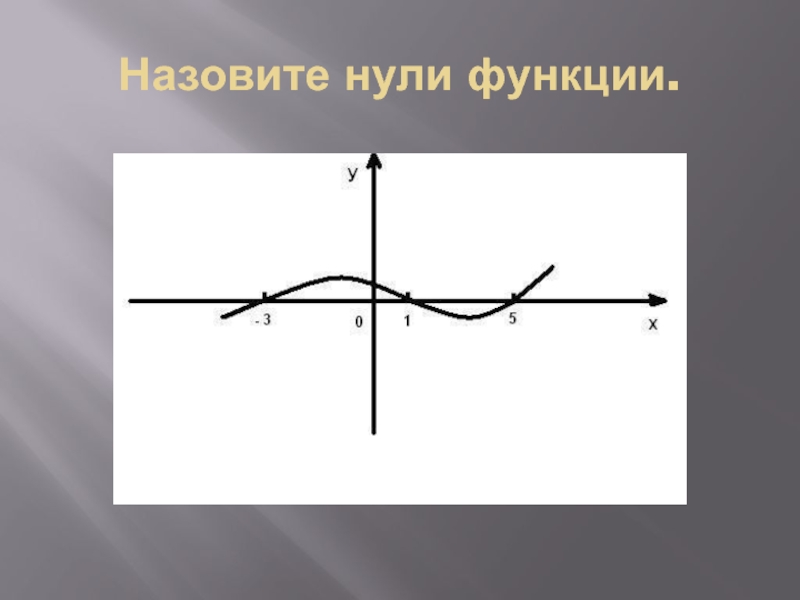
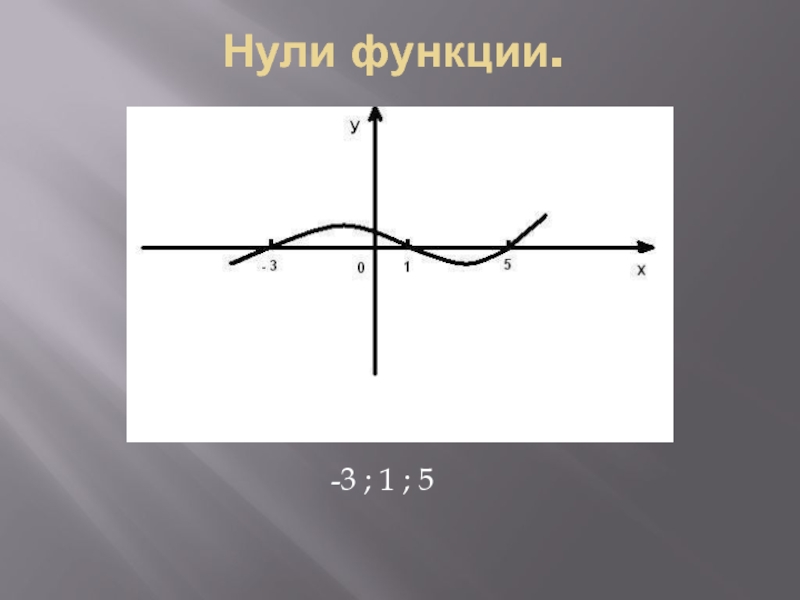
- 2. Назовите нули функции.
- 3. Нули функции. -3 ; 1 ; 5
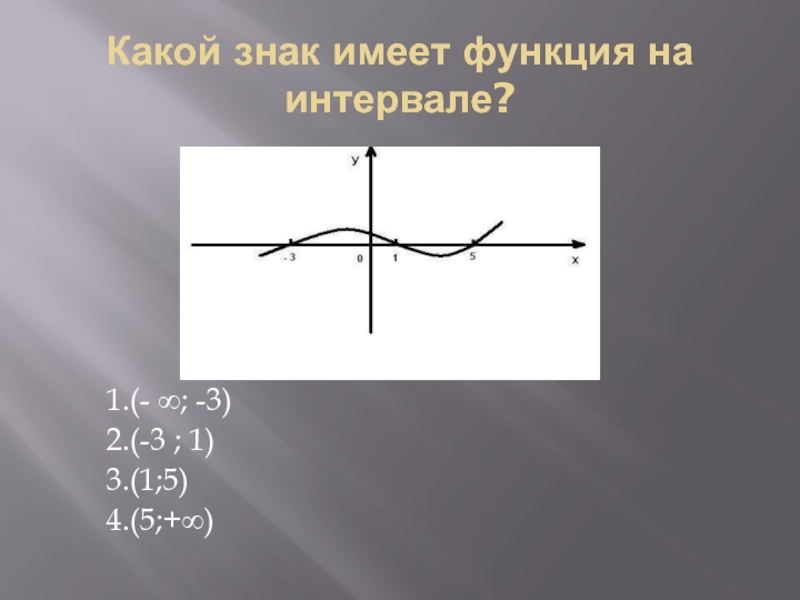
- 4. Какой знак имеет функция на интервале?1.(- ∞; -3)2.(-3 ; 1)3.(1;5)4.(5;+∞)
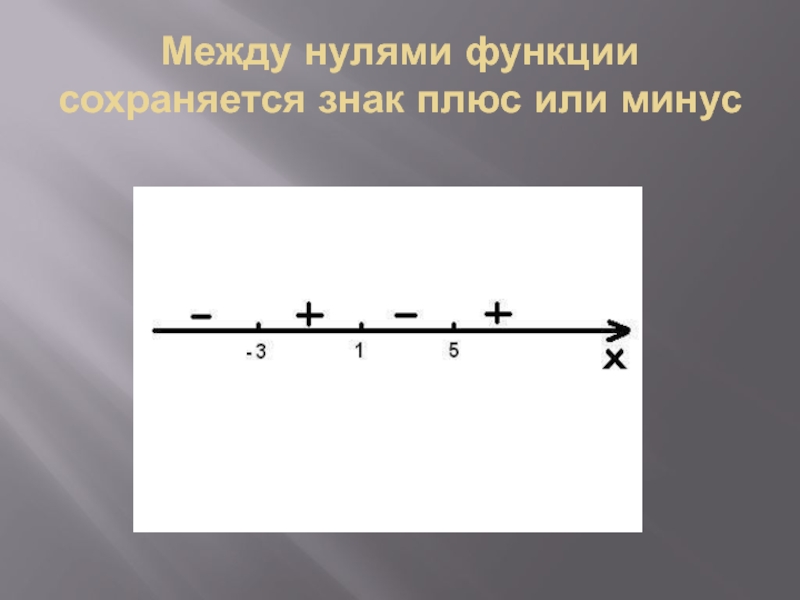
- 5. Между нулями функции сохраняется знак плюс или минус
- 6. Решите неравенство:x² - 4 ≥ 0Какую функцию нам необходимо рассмотреть?
- 7. Решите неравенство:x² - 4 ≥ 0Какую функцию нам необходимо рассмотреть?f (x)=x² - 4
- 8. Решите неравенство:x² - 4 ≥ 0Назовите нули функции.
- 9. Решите неравенство:x² - 4 ≥ 0Назовите нули функции.x = 2x = - 2
- 10. Решите неравенство:x² - 4 ≥ 0Нанесём нули
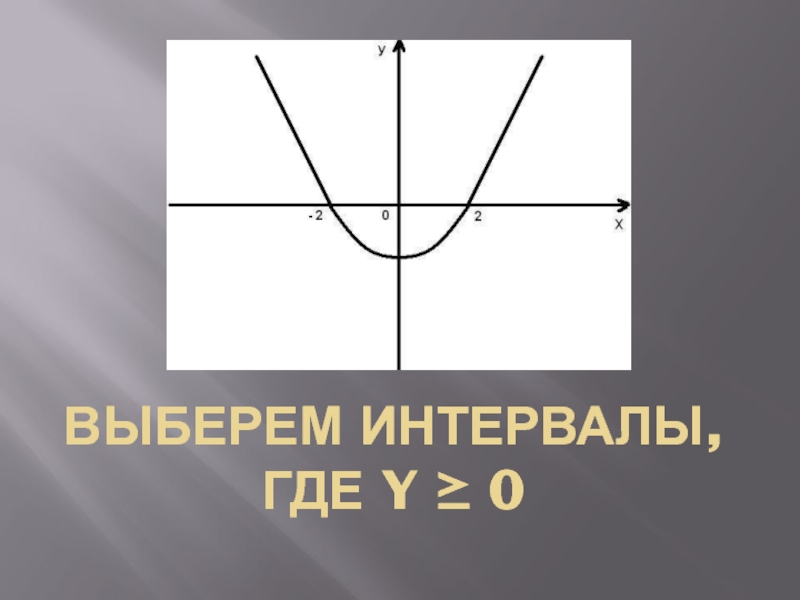
- 11. Выберем интервалы, где y ≥ 0
- 12. Выберем интервалы, где y ≥ 0 xϵ(-∞; -2] U [2;+∞).
- 13. Всё решение.x² - 4 ≥ 0f (x)=x²
- 14. Решите методом интервалов неравенство.
- 15. Решите методом интервалов неравенство.
- 16. Решите методом интервалов неравенство.
- 17. Решите методом интервалов неравенство.
- 18. Решите методом интервалов неравенство.
- 19. Решите методом интервалов неравенство.
- 20. Решите методом интервалов неравенство.
- 21. Решите методом интервалов неравенство.
- 22. Скачать презентанцию
Назовите нули функции.
Слайды и текст этой презентации
Слайд 1Решение неравенств второй степени с одной переменной. 9 класс. Рыжкова Л.А. школа 1502
при МЭИ
Слайд 10Решите неравенство:
x² - 4 ≥ 0
Нанесём нули функции на координатную
плоскость и определим какие промежутки нужно выбрать.
![Выберем интервалы, где y ≥ 0 xϵ(-∞; -2] U [2;+∞).](/img/thumbs/20b5170f7f84c63ea0f7267a91cc0c3b-800x.jpg "Решение неравенств второй степени с одной переменной Выберем интервалы, где y ≥ 0 xϵ(-∞; -2] U [2;+∞).")
Слайд 16
Решите методом интервалов неравенство.
(
x – 5 )( 4 – 2x ) ≥ 0f (x)=( x – 5 )( 4 – 2x )
( x – 5 )( 4 – 2x ) = 0
Слайд 17
Решите методом интервалов неравенство.
(
x – 5 )( 4 – 2x ) ≥ 0f (x)=( x – 5 )( 4 – 2x )
( x – 5 )( 4 – 2x ) = 0
x = 5 x = 2
Слайд 18
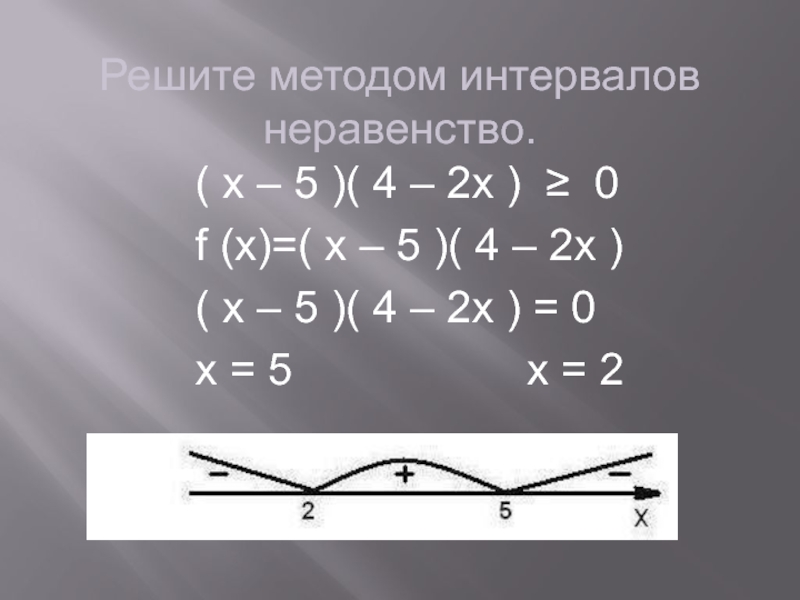
Решите методом интервалов неравенство.
(
x – 5 )( 4 – 2x ) ≥ 0f (x)=( x – 5 )( 4 – 2x )
( x – 5 )( 4 – 2x ) = 0
x = 5 x = 2
Нанесём нули функции на координатную прямую, и вспомним правило расстановки знаков внутри
промежутков.
Слайд 19
Решите методом интервалов неравенство.
(
x – 5 )( 4 – 2x ) ≥ 0f (x)=( x – 5 )( 4 – 2x )
( x – 5 )( 4 – 2x ) = 0
x = 5 x = 2
Слайд 20
Решите методом интервалов неравенство.
(
x – 5 )( 4 – 2x ) ≥ 0f (x)=( x – 5 )( 4 – 2x )
( x – 5 )( 4 – 2x ) = 0
x = 5 x = 2
Слайд 21
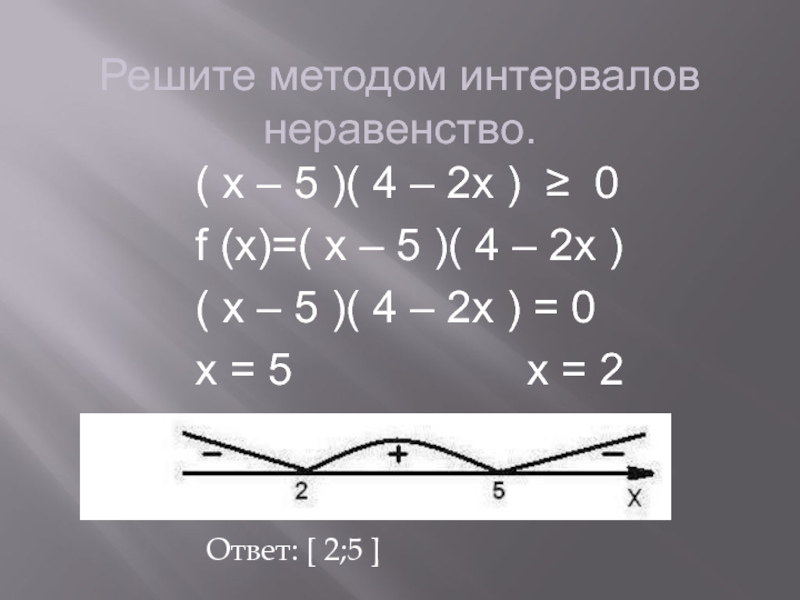
Решите методом интервалов неравенство.
(
x – 5 )( 4 – 2x ) ≥ 0f (x)=( x – 5 )( 4 – 2x )
( x – 5 )( 4 – 2x ) = 0
x = 5 x = 2
Ответ: [ 2;5 ]
