Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теорема Пифагора
Содержание
- 1. Теорема Пифагора
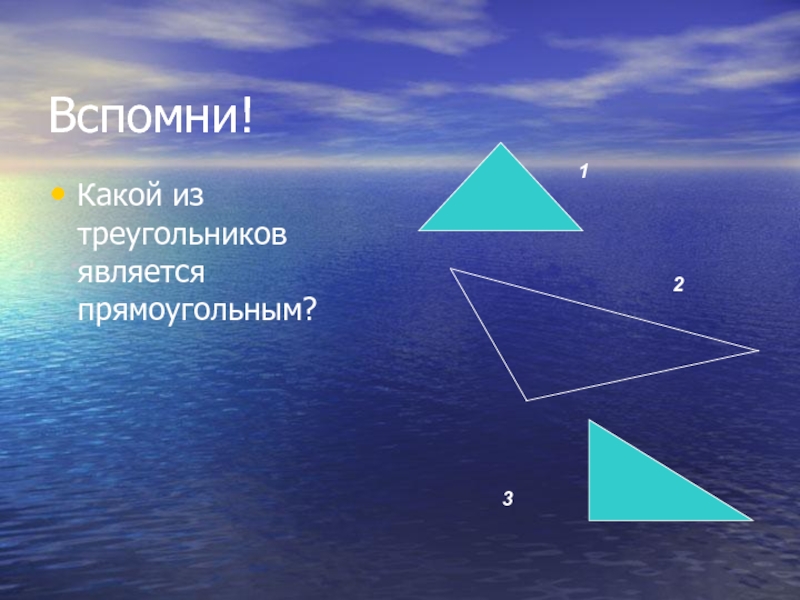
- 2. Вспомни!Какой из треугольников является прямоугольным?123
- 3. Какая из сторон прямоугольного треугольника является гипотенузой?123
- 4. Какой из отрезков является высотой прямоугольного треугольника?2 13
- 5. Какие отрезки являются проекциями катетов на гипотенузу?123
- 6. Какие из соотношений справедливы в прямоугольном треугольнике?1.
- 7. В прямоугольном треугольнике квадрат гипотенузы равен сумме
- 8. В прямоугольном треугольнике квадрат гипотенузы равен сумме
- 9. Историческая справкаПифагор жил в Древней Греции (родился
- 10. Найди АВ90о12Х АВДЕ
- 11. Реши задачу:Над озером тихим, с полфута размером,
- 12. Решение задачи:ВСДХСД – глубина озера, обозначим ее
- 13. Теорема ПифагораРефлексия:Значение теоремы ПифагораАктуализация Теорема Пифагора и ее доказательствоИсторическая справкаПонимание
- 14. Скачать презентанцию
Вспомни!Какой из треугольников является прямоугольным?123
Слайды и текст этой презентации
Слайд 1Теорема Пифагора
План:
Значение теоремы Пифагора
Актуализация
Теорема Пифагора и ее доказательство
Историческая справка
Понимание
Слайд 6Какие из соотношений справедливы в прямоугольном треугольнике?
1. а2= а1 с
2.
b2 = b1 с
3. с2 = а1 b1
b1
а1
с
b
а
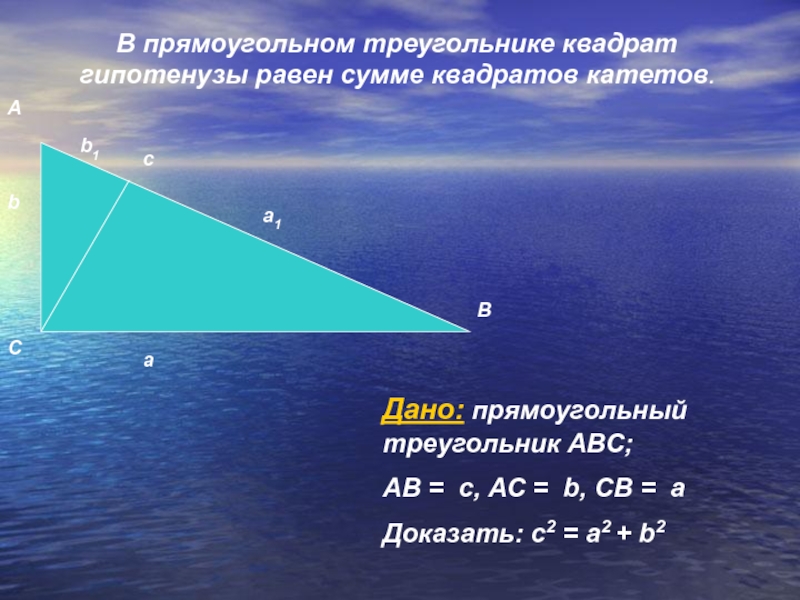
Слайд 7В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
b1
а1
с
а
b
В
С
А
Дано: прямоугольный
треугольник АВС;
АВ = с, АС = b, СВ = а
Доказать:
с2 = а2 + b2
Слайд 8В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
b1
а1
с
а
b
В
С
А
Дано: прямоугольный
треугольник АВС;
АВ = с, АС = b, СВ = а
Доказать:
с2 = а2 + b2Доказательство: по теореме о соотношениях в прямоугольном треугольнике справедливы следующие равенства: а2= а1 с
b2 = b1 с
Сложим почленно эти выражения:
b2+ а2 = с b1 + а1 c = с(b1 + а1) = с2
Вывод: с2= а2+ b2
Слайд 9Историческая справка
Пифагор жил в Древней Греции (родился он около 580
г до н.э. , а умер в 500 г. до
н.э.)http://www.1september.ru/ru/mat/2001/24/no24_01.htm
http://center.fio.ru/works_student/TerentevAV/b_p2.htm
Слайд 11Реши задачу:
Над озером тихим, с полфута размером, высился лотоса цвет.
Он
рос одиноко. И ветер порывом
Отнес его в сторону. Нет
Боле цветка
над водой.Нашел же рыбак его ранней весной
В двух футах от места, где рос.
Итак, предложу я вопрос:
Как озера вода здесь глубока.
Слайд 12Решение задачи:
В
С
Д
Х
СД – глубина озера, обозначим ее Х.
Тогда по теореме
Пифагора имеем:
ВД2 – Х2 = ВС2, т.е.
(Х + 1/2)2 –
Х2 = 22,Х2 + Х + ¼ - Х2 = 4,
Х = 3 ¾ (фут).
Слайд 13Теорема Пифагора
Рефлексия:
Значение теоремы Пифагора
Актуализация
Теорема Пифагора и ее доказательство
Историческая справка
Понимание
