Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация к уроку на тему "Пирамида"
Содержание
- 1. Презентация к уроку на тему "Пирамида"
- 2. Евклид ок. 300 г. до н. э
- 3. Герон I-II вв. н. э.
- 4. Это многогранник, у которого
- 5. Лежандр 1752-1833 Это телесная фигура, образованная треугольниками,
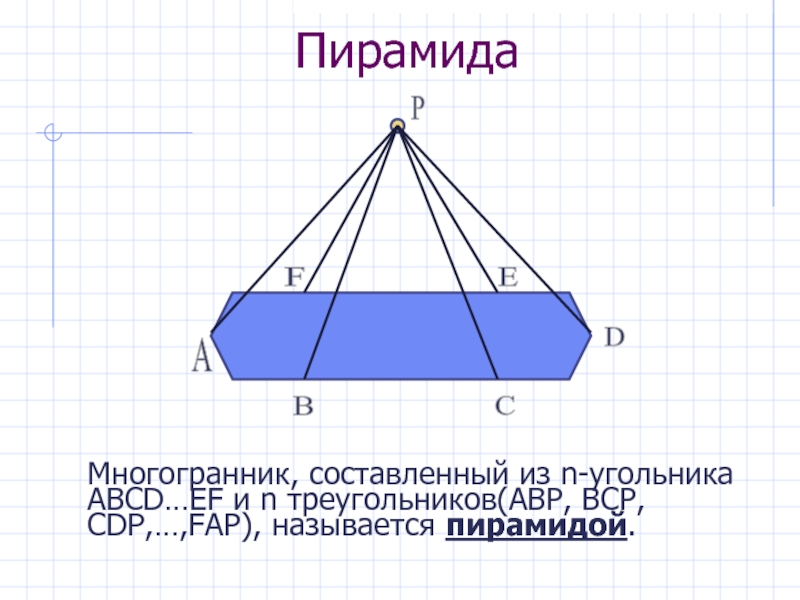
- 6. ПирамидаМногогранник, составленный из n-угольника АВСD…EF и n треугольников(АВР, ВСР, СDР,…,FAP), называется пирамидой.
- 7. Призма
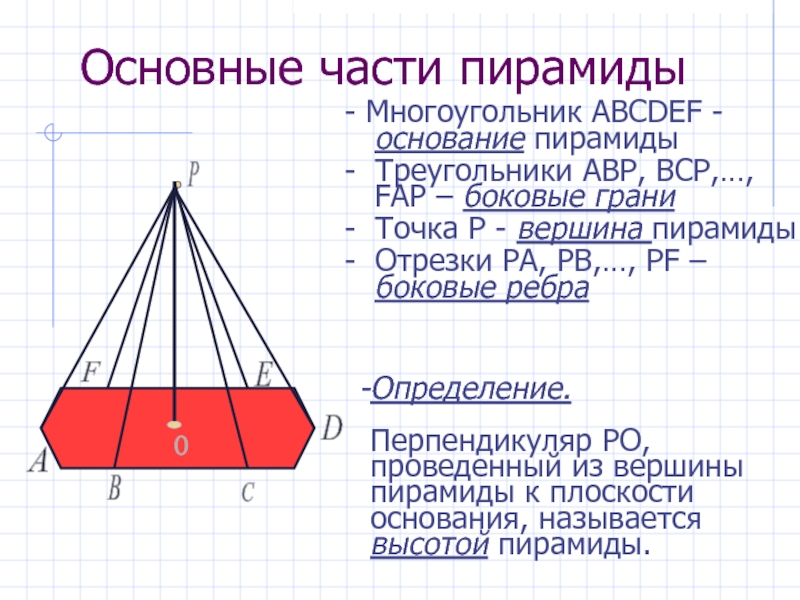
- 8. Основные части пирамиды- Многоугольник АВСDEF - основание
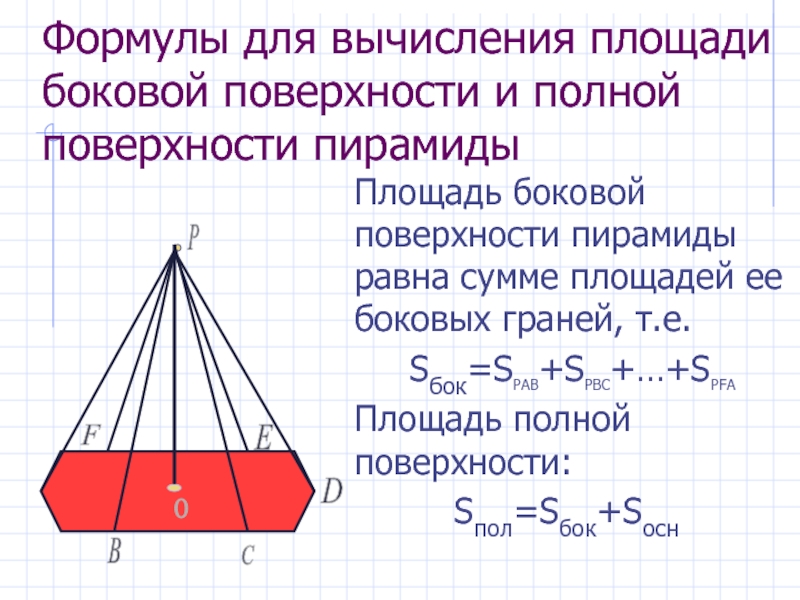
- 9. Формулы для вычисления площади боковой поверхности и
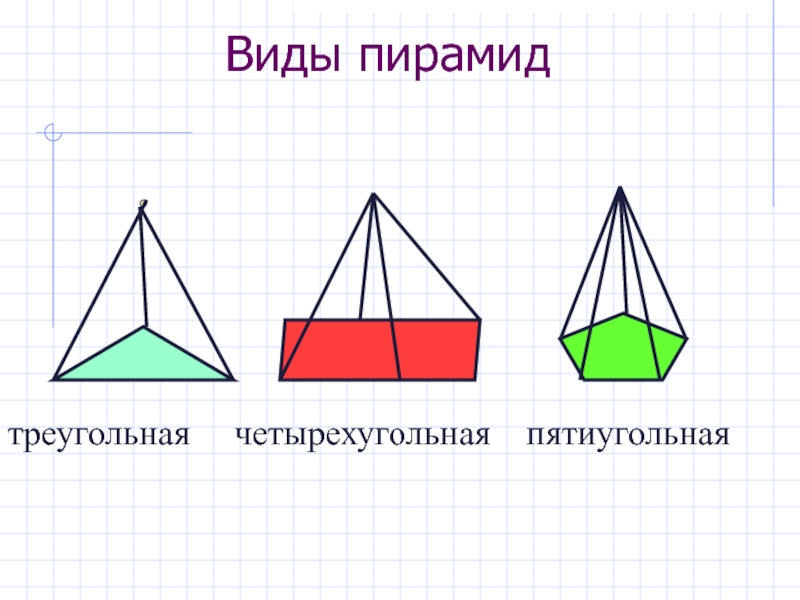
- 10. Виды пирамидтреугольная четырехугольная пятиугольная
- 11. 12345
- 12. Правильная пирамидаПирамида называется правильной, если ее основание
- 13. Слайд 13
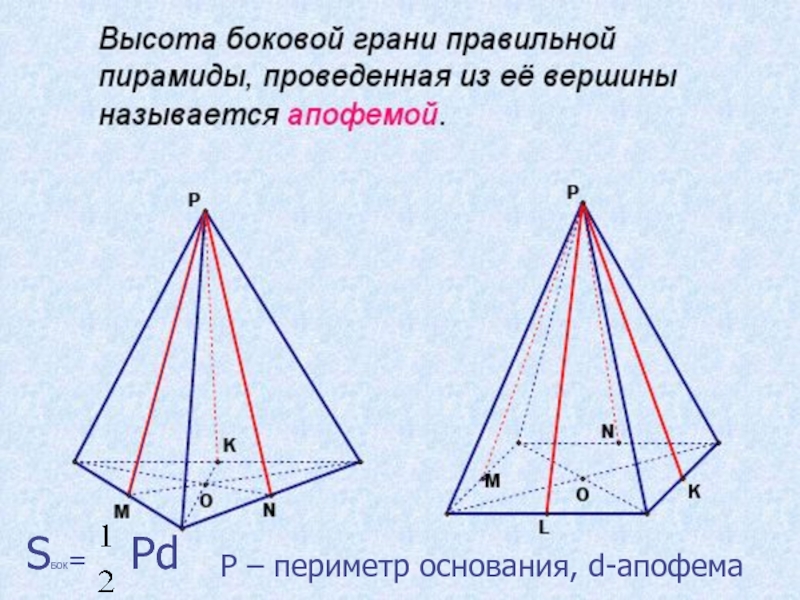
- 14. P – периметр основания, d-апофема
- 15. Домашнее задание § 2, п.28, 29(доказательство теоремы)№ 240, 254Дополнительно Материал о свойствах пирамид
- 16. Задача 1. Сторона основания правильной треугольной пирамиды 16,боковое ребро 10. Найдите площадь боковой поверхности пирамиды.
- 17. Задача 2. В основании пирамиды Хеопса –
- 18. Всем спасибо за урок!
- 19. Скачать презентанцию
Евклид ок. 300 г. до н. э Это телесная фигура, ограниченная плоскостями, которые от одной плоскости (основания) сходятся к одной точке (вершине)
Слайды и текст этой презентации
Слайд 3Герон
I-II вв. н. э.
Это фигура, ограниченная треугольниками, сходящимися в одной
точке, и основанием, которым служит многоугольникСлайд 4 Это многогранник, у которого все грани, кроме
одной, сходятся в одной точке
Тейлор Брук
1685-1731
Слайд 5Лежандр
1752-1833
Это телесная фигура, образованная треугольниками, сходящимися в
одной точке и заканчивающаяся по различным сторонам
плоского основанияСлайд 6Пирамида
Многогранник, составленный из n-угольника АВСD…EF и n треугольников(АВР, ВСР, СDР,…,FAP),
называется пирамидой.
Слайд 8Основные части пирамиды
- Многоугольник АВСDEF - основание пирамиды
- Треугольники АВР,
ВСР,…, FAP – боковые грани
- Точка Р - вершина пирамиды
-
Отрезки РА, РВ,…, РF – боковые ребраА
В
С
D
E
F
P
О
Определение.
Перпендикуляр РО, проведенный из вершины пирамиды к плоскости основания, называется высотой пирамиды.
Слайд 9Формулы для вычисления площади боковой поверхности и полной поверхности пирамиды
Площадь
боковой поверхности пирамиды равна сумме площадей ее боковых граней, т.е.
Sбок=SРАВ+SРВС+…+SPFAПлощадь полной поверхности:
Sпол=Sбок+Sосн
Слайд 12Правильная пирамида
Пирамида называется правильной, если ее основание – правильный многоугольник,
а отрезок, соединяющий вершину пирамиды с центром основания, является ее
высотой
R
R
r
О
Слайд 15Домашнее задание
§ 2, п.28, 29
(доказательство теоремы)
№ 240, 254
Дополнительно
Материал
о свойствах пирамид
Слайд 16Задача 1. Сторона основания правильной треугольной пирамиды 16,боковое ребро 10.
Найдите площадь боковой поверхности пирамиды.
Слайд 17Задача 2. В основании пирамиды Хеопса – квадрат со стороной
230 м. Основание высоты пирамиды лежит в центре квадрата. Тангенс
угла наклона боковой грани к основанию равен 1,2. Найдите высоту самой высокой египетской пирамидыhttp://reshuege.ru/test?theme=177