Решение планиметрических задач (уровень С)

Содержание

1. Решение планиметрических задач (уровень С)
2. Решение геометрических задач трудно
3. Задача 1 Дан ромб
4. РешениеРешение
5. ВС = а,
6. Аналогично из ∆ KNCR = KN =
7. Задача 2В треугольнике со сторонами 6, 12,
8. РешениеВ∆ АВС – прямоугольный так как
9. Поэтому
10. Задача 3В четырехугольнике АВСD АВ = 5
11. РешениеАВСDЕ301205 см3 см8 смПродолжим стороны ВС и
12. или 5 = 8
13. Скачать презентанцию

Решение геометрических задач трудно дается учащимся, так как требуют развитого абстрактного мышления, умения видеть и чувствовать чертеж. Их особенностью является рассмотрение различных конфигураций геометрических фигур. Д ля их

Главная
Математика
Решение планиметрических задач (уровень С)

Слайды и текст этой презентации

Слайд 1

Решение планиметрических задач
( уровень С)
Муниципальное образовательное учреждение

основная общеобразовательная школа №7 г.о. Тольятти
учитель математики высшей категории

Холова Сания Минзакировна

Решение планиметрических задач ( уровень С)Муниципальное образовательное учреждение основная общеобразовательная школа №7 г.о. Тольятти учитель

Слайд 2 Решение геометрических задач трудно дается
учащимся,

так как требуют развитого абстрактного
мышления, умения видеть и чувствовать

чертеж.
Их особенностью является рассмотрение различных конфигураций геометрических фигур.
Д ля их решения необходимо знать множество
формул, теорем, свойств и определений.
Представленные ниже задачи можно рассматривать
на уроке, отведенном для подготовки учащихся к ЕГЭ.

Решение геометрических задач трудно дается учащимся, так как требуют развитого абстрактного мышления, умения видеть

Слайд 3
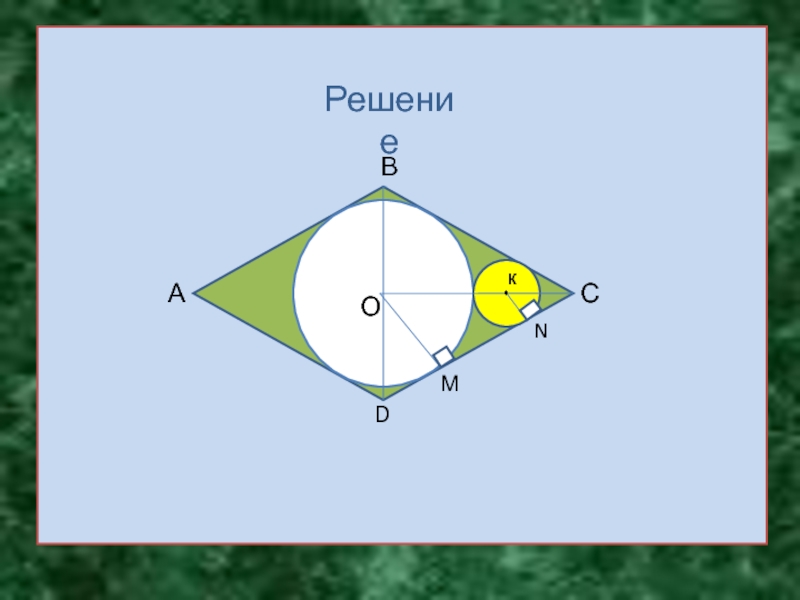
Задача 1

Дан ромб со стороной a

и одним из углов в 60. В этот ромб вписана

окружность S. В угол ромба, равный 60, вписана окружность так, что она касается окружности S. Найдите радиус этой окружности.

Задача 1 Дан ромб со стороной a и одним из углов в 60. В

Слайд 4Решение
Решение

Слайд 5ВС = а, ВСD = 60.
Центры

данной окружности О и искомой К лежат на биссектрисе угла

ВСD, так как они равноудалены от сторон ВС и DС ромба.
Из ∆ ВОС
ОС = ВС ∙ cos ВОС = а ∙ cos30 = .
Из ∆МОС
R = ОС ∙ sin ОСD = ∙ sin30 = .

ВС = а, ВСD = 60.Центры данной окружности О и искомой К лежат

Слайд 6Аналогично из ∆ KNC
R = KN = KC ∙ sin30

= KC, но КС = ОС – (R +

r).
Получили уравнение
r = ( - R – r). Отсюда
3r = , r = .
Ответ: радиус искомой окружности равен r =

Аналогично из ∆ KNCR = KN = KC ∙ sin30 = KC, но КС = ОС

Слайд 7Задача 2
В треугольнике со сторонами 6, 12, 3

, две меньшие стороны являются касательными к окружности, центр которой

лежит на большей стороне. Найдите радиус этой окружности.

Задача 2В треугольнике со сторонами 6, 12, 3 , две меньшие стороны являются касательными к

Слайд 8
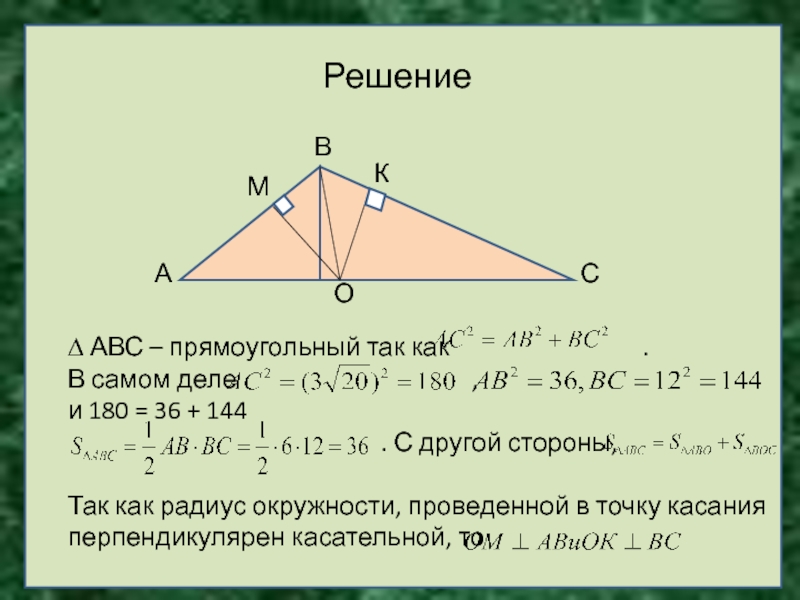
Решение

В
∆ АВС – прямоугольный так как

.
В самом деле , и 180 = 36 + 144
. С другой стороны,

Так как радиус окружности, проведенной в точку касания перпендикулярен касательной, то

Слайд 9
Поэтому

Итак, 3r + 6r = 36 r = 4.
Ответ: радиус окружности равен 4.

Слайд 10
Задача 3
В четырехугольнике АВСD АВ = 5 см,
ВС

= 3 см, АD = 8 см,

А = 30 , В = 120 .
Найти сторону СD.

Слайд 11
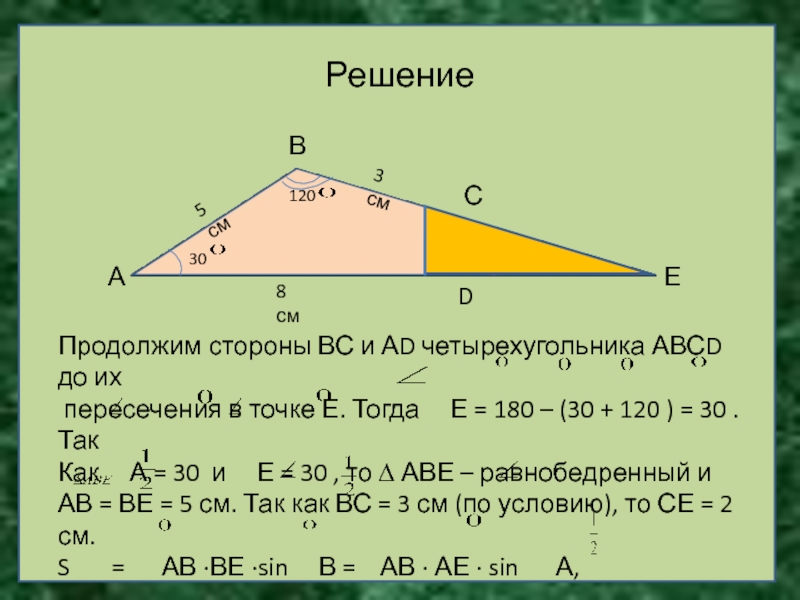
Решение

А
В
С
D
Е
30
120

5 см
3 см
8 см
Продолжим стороны ВС и АD четырехугольника АВСD

до их
пересечения в точке Е. Тогда Е

= 180 – (30 + 120 ) = 30 . Так
Как А = 30 и Е = 30 , то ∆ АВЕ – равнобедренный и
АВ = ВЕ = 5 см. Так как ВС = 3 см (по условию), то СЕ = 2 см.
S = АВ ∙ВЕ ∙sin В = АВ ∙ АЕ ∙ sin А,

5 sin 120 = АЕ ∙sin 30 , или 5 cos 30 = (8+ DЕ)∙ ,