Решение тригонометрических неравенств графическим способом

сложный (отличен от х), то заменяем его на t.
2. Строим в одной

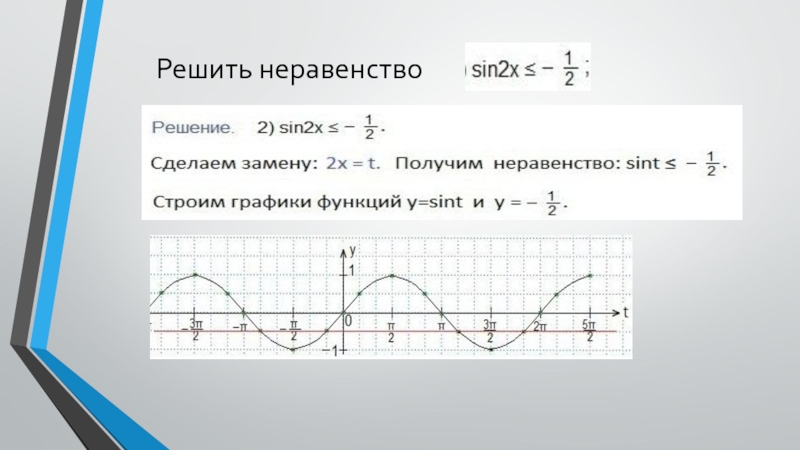
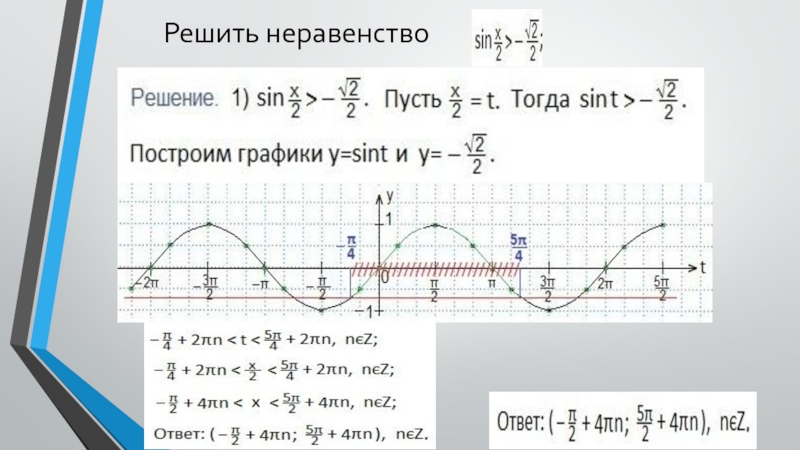
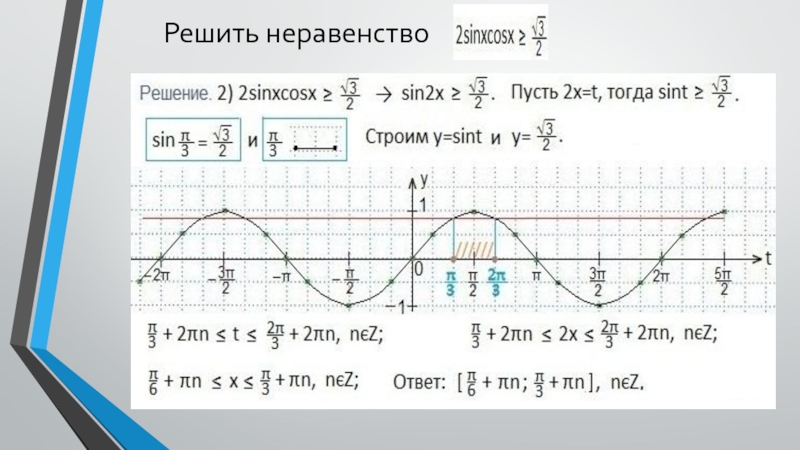
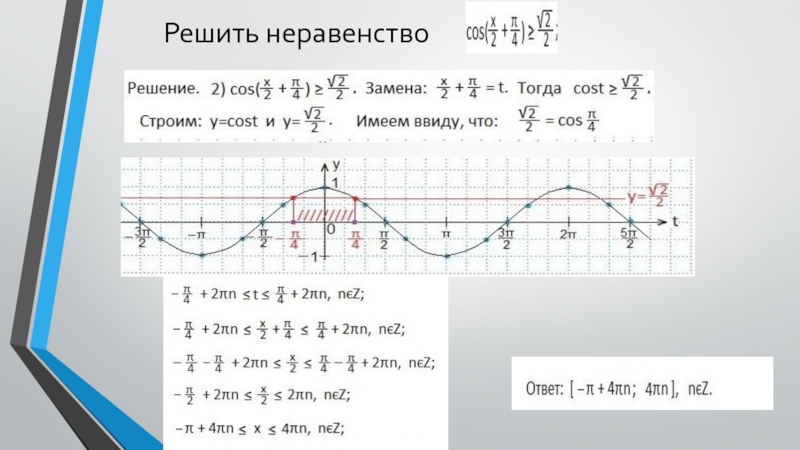
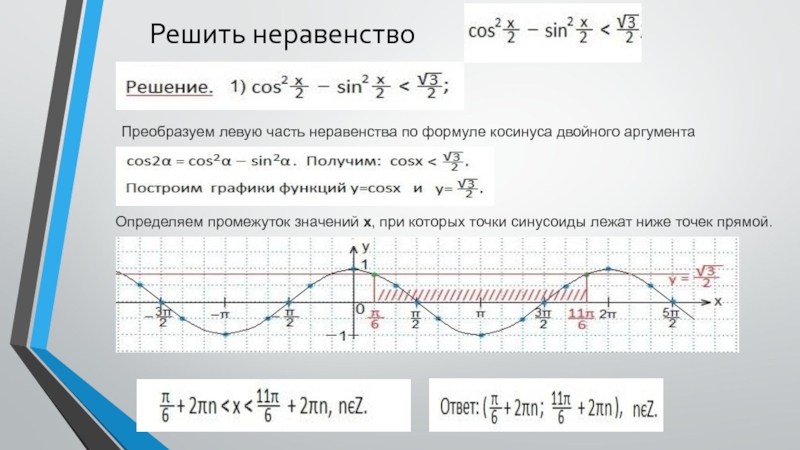
координатной плоскости tOy графики функций y=sint  и y=a.
3. Находим такие две соседние точки пересечения графиков (поближе к оси Оу), между которыми синусоида располагается ниже прямой у=а. Находим абсциссы этих точек.
4. Записываем двойное неравенство для аргумента t, учитывая период синуса (t будет между найденными абсциссами).
5. Делаем обратную замену (возвращаемся к первоначальному аргументу) и выражаем значение х из двойного неравенства, записываем ответ в виде числового промежутка.

Тогда по горизонтальной оси Ох значение π (≈3,14) составит шесть клеток. Рассчитываем остальные значения

аргументов (в клетках

синусоиды, которая лежит ниже данной прямой, а значит, промежуток между

этими выделенными точками удовлетворяет данному неравенству. Учтем период синуса, запишем результат в виде двойного неравенства, а ответ в виде числового промежутка.

промежуток значений х, при которых точки синусоиды лежат ниже точек прямой.

< t < arcsin a + 2πn,  nєZ.

arcsin a + 2πn, nєZ.

2π — arccos a + 2πn, nєZ.

+ 2πn, nєZ.
.
Применяйте  формулы для решения тригонометрических неравенств, и вы

 сэкономите время на экзаменационном тестировании.

Если  cost>a, (-1≤а≤1), то