Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Синус и косинус
Содержание
- 1. Синус и косинус
- 2. Цель работы: в моей презентации мы познакомимся
- 3. Немного о синусе.Синусом острого угла прямоугольного треугольника
- 4. Немного о косинусе.Косинусом острого угла прямоугольного треугольника
- 5. Немного о тангенсе.Тангенсом острого угла прямоугольного треугольника
- 6. Основные тригонометрические тождества и формулы приведения. Также
- 7. Теорема синусов и ее доказательсво.Теорема: стороны треугольника
- 8. Доказательство:По теореме о площади треугольника S=1/2 ab
- 9. Теорема косинусов.Теорема: квадрат стороны треугольника равен сумме
- 10. Доказательство:Введем систему координат с началом в точке
- 11. 1. По теореме косинусов находим с :
- 12. Задача №2Дано:
- 13. 1. угол А= 180- угол В- угол
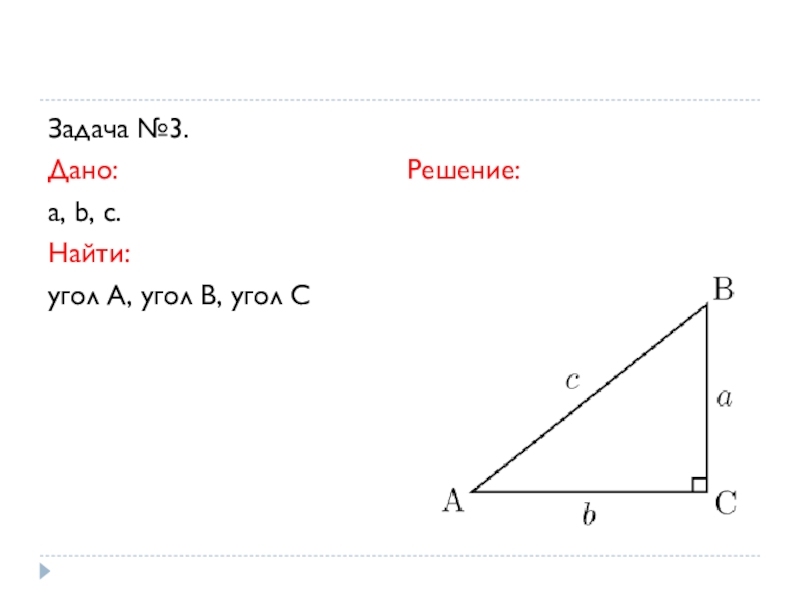
- 14. Задача №3.Дано:
- 15. 1.Пользуясь теоремой косинусов, получаем:Угол А находим с
- 16. Спасибо за внимание!
- 17. Скачать презентанцию
Цель работы: в моей презентации мы познакомимся с синусом, косинусом и тангенсом, узнаем о формулах приведения, основных тригонометрических тождествах, теореме косинусов и синусов и их применении.
Слайды и текст этой презентации
Слайд 2Цель работы: в моей презентации мы познакомимся с синусом, косинусом
и тангенсом, узнаем о формулах приведения, основных тригонометрических тождествах, теореме
косинусов и синусов и их применении.
Слайд 3Немного о синусе.
Синусом острого угла прямоугольного треугольника называется отношение противолежащего
катета к гипотенузе.
sinA=BC/AB
sin30=1/2
sin45=√2/2
sin60=√3/2
Слайд 4Немного о косинусе.
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего
катета к гипотенузе.
cosA=AC/ABсos30=√3/2
сos45=√2/2
сos60=1/2
Слайд 5Немного о тангенсе.
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего
катета к прилежащему катету.
tgA=BC/ACtg30=√3/3
tg45=1
tg60=√3
Слайд 6Основные тригонометрические тождества и формулы приведения.
Также справедливы следующие тождества:
sin(90-ἀ)=cosἀ
, cos(90-ἀ)=sinἀ при 0≤ἀ≤90.
sin(180-ἀ)=sinἀ, cos(180-ἀ)=-cosἀ при 0≤ἀ≤180.
Эти тождества называются формулы
приведения
Слайд 7Теорема синусов и ее доказательсво.
Теорема: стороны треугольника пропорциональны синусам противолежащих
углов.
Доказательство.Дано:
∆АВС АВ=с
ВС=а
СА=b
Док-ть:
а/sinA=b/sinB=c/sinC
Слайд 8Доказательство:
По теореме о площади треугольника S=1/2 ab sinC, S=1/2bc sinA,
S=1/2ca sinB/. Из первых двух равенств получаем 1/2ab sinC=1/2bc sinA,
откуда a/sinA=c/sinC. Точно так же из второго и третьего равенств следует a/sinA=b/sinB. Итак, a/sinA=b/sinB=c/sinC. Теорема доказана.
Слайд 9Теорема косинусов.
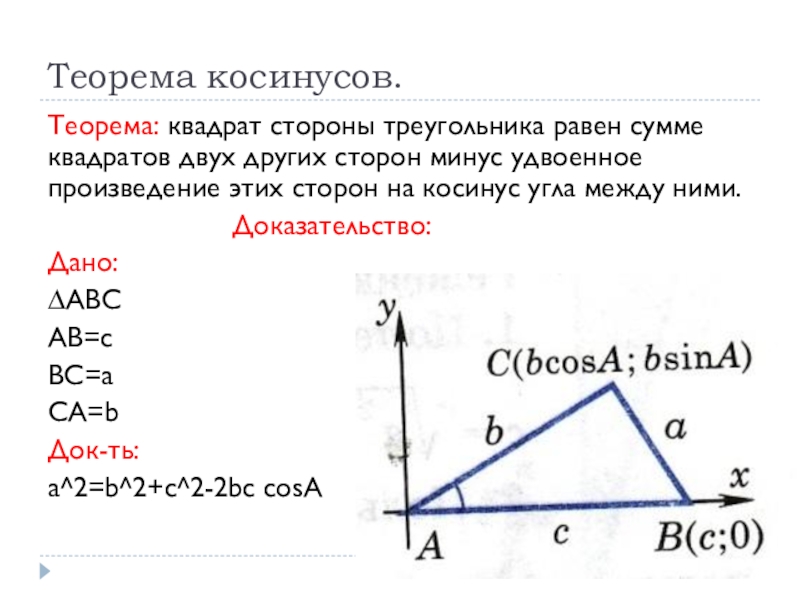
Теорема: квадрат стороны треугольника равен сумме квадратов двух других
сторон минус удвоенное произведение этих сторон на косинус угла между
ними.Доказательство:
Дано:
∆ABC
AB=c
BC=a
CA=b
Док-ть:
a^2=b^2+c^2-2bc cosA
Слайд 10Доказательство:
Введем систему координат с началом в точке А так, как
показано на рисунке. Тогда точка В имеет координаты (с;0), а
точка С имеет координаты (b cosA, b sinA). По формуле расстояния между двумя точками получаем:BC^2=a^2=(b cosA-c)
^2+b^2sin^2A=b^2cos^2A+b^2sin^2A-2bc cosA+c^2=b^2+c^2-2bc cosA.
Слайд 111. По теореме косинусов находим с :
c² =а² + b²-2ab cosἀ
2.Пользуясь теоремой косинусов получаем:
3. Угол А находим с помощью миркокалькулятора или по таблице.
Угол В=180-угол А- угол С.
Слайд 131. угол А= 180- угол В- угол С.
2. С помощью
теоремы синусов вычисляем b и с:
b=a(sinB/sinA) , c=a(sinC/sinA)
Слайд 151.Пользуясь теоремой косинусов, получаем:
Угол А находим с помощью микрокалькулятора или
по таблице.
2. Аналогично находим угол В.
3. Угол С= 180-угол А-
угол В.
