Система координат в пространстве

Содержание

1. Система координат в пространстве
2. Вспомним, как определяется координатная(числовая) прямая.Изображаем произвольную прямую;х01МаТогда
3. А теперь, что мы подразумеваем под координатной плоскостью.ух011МаbM(a; b)
4. xyz01Ox ⊥ Oy ⊥ OzOx – ось
5. xyz0111 Координатные плоскости:OxzOxyOyz
6. Координатные плоскости:xz⊥xy⊥yz
7. Положение любой точки в пространстве определяется тремя
8. xy11AAyzAxzAxyAxAyz12) Далее, в плоскости Oxy, из точки
9. xy11AAyzAxzAxyAxAyz14) Таким образом, мы получили ортогональные проекции
10. xy0111AAyzAxzAxyAxAzAyzТогда, AAx ⊥ Ox, AAy ⊥ Oy
11. xy0111AAyzAxzAxyAxAzAyzКоординаты точки можно понимать как линейные размеры
12. 1xyz011232Пример 1. Изобразить точки A(1; 2; 3),
13. xyz011A1232A(1; 2; 3)B−2B(−2; 2; 1)C(2; −2; − 3)C−22−3Проследите и самостоятельно сформулируйте построение точек B и C.
14. 1). Если одна из координат точки равна
15. xyz011A1abcПусть A(a; b; c)−a−b−cA0Построим точку A0, симметричную
16. xyz011A1abcПусть A(a; b; c)−c−bA1Построим точку A1, симметричную
17. xyz011A1abcПусть A(a; b; c)−c−aA2Построим точку A2, симметричную
18. xyz011A1abcПусть A(a; b; c)−a−bA3Построим точку A3, симметричную
19. xyz011A1abcПусть A(a; b; c)−cA4Построим точку A4, симметричную
20. xyz011A1abcПусть A(a; b; c)−bA5Построим точку A5, симметричную
21. xyz011A1abcПусть A(a; b; c)A69). Тогда координаты точки
22. xy011Az1Расстояние между точками A(x1; y1; z1) и B(x2; y2; z2)Bx1x2y1y2z1z2|x1–x2||y1–y2||z1–z2|C
23. xy011Az1Координаты середины отрезка АВ, где A(x1; y1; z1) и B(x2; y2; z2)Bx1x2y1y2z1z2M
24. Скачать презентанцию

Вспомним, как определяется координатная(числовая) прямая.Изображаем произвольную прямую;х01МаТогда любой точке этой координатной прямой соответствует единственное действительной число a. И наоборот, любое действительное число может быть изображено единственной соответствующей точкой, для которой это

Главная
Математика
Система координат в пространстве

Слайды и текст этой презентации

Слайд 1Геометрия, 11 класс
Система координат в пространстве
Воробьев Леонид Альбертович, г.Минск

Слайд 2Вспомним, как определяется координатная(числовая) прямая.
Изображаем произвольную прямую;
х
0
1

М
а
Тогда любой точке этой

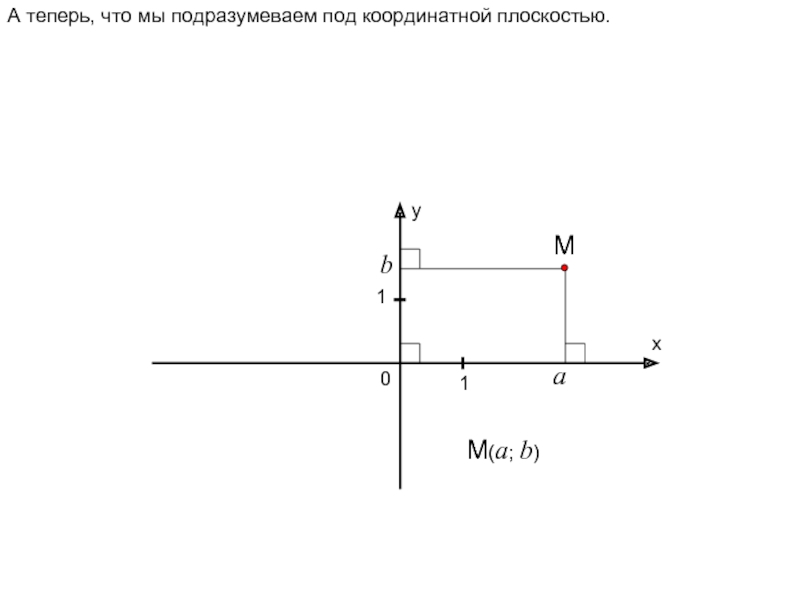
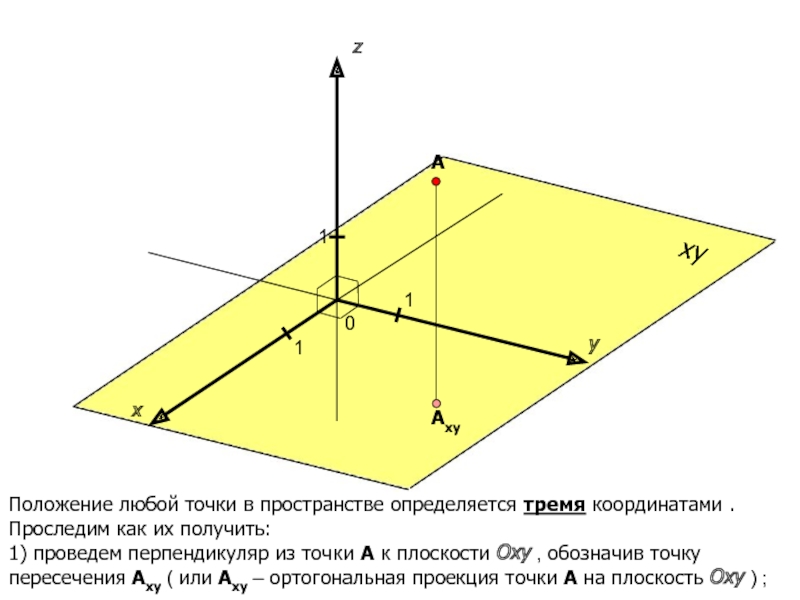
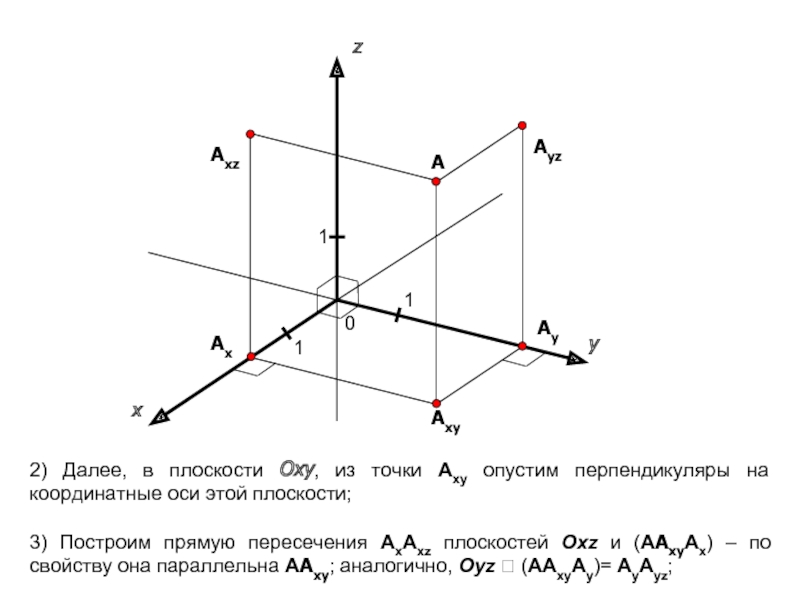
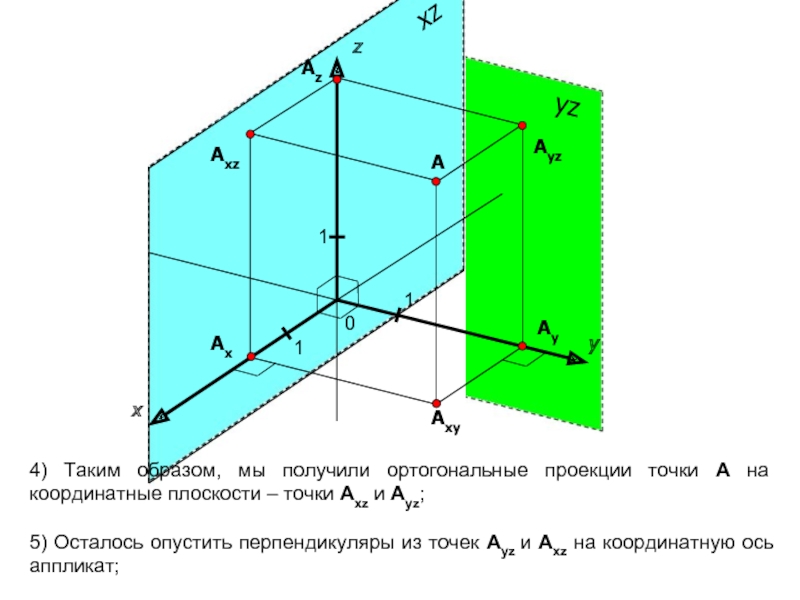
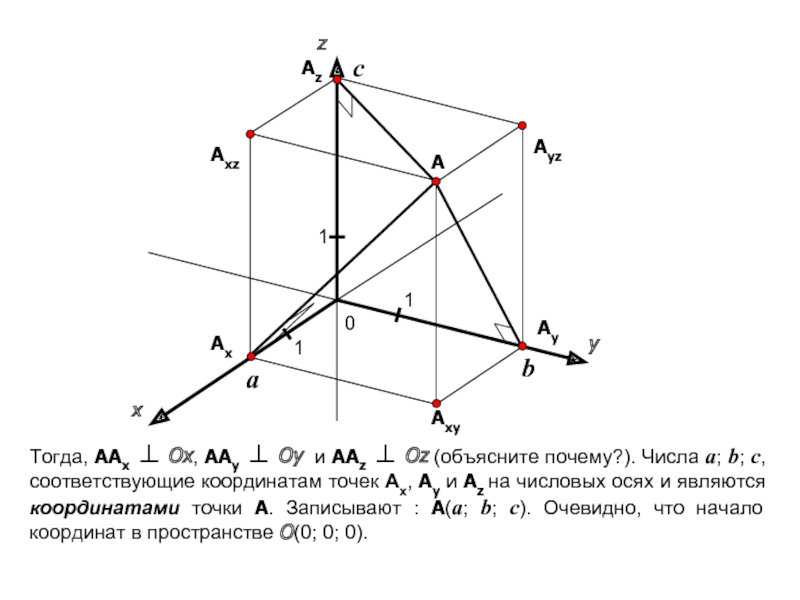
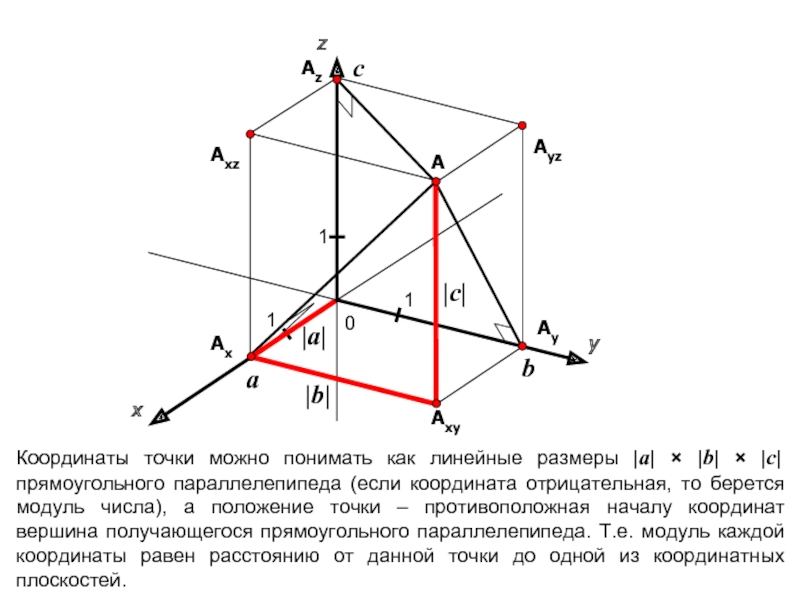
координатной прямой соответствует единственное действительной число a. И наоборот, любое

действительное число может быть изображено единственной соответствующей точкой, для которой это число является координатой. Записывают: M(a).

2) Придаем ей положительное направление и обозначаем её;

3) Выбираем произвольную точку за начало отсчета;

4) Определяем длину единичного отрезка (масштаб).

Вспомним, как определяется координатная(числовая) прямая.Изображаем произвольную прямую;х01МаТогда любой точке этой координатной прямой соответствует единственное действительной число a.

Слайд 3А теперь, что мы подразумеваем под координатной плоскостью.
у
х
0
1
1

М
а
b
M(a; b)

Слайд 4x
y
z
0
1
Ox ⊥ Oy ⊥ Oz
Ox – ось абсцисс
Oy – ось

ординат
Oz – ось аппликат
Координатные оси:
Выберем в пространстве три попарно перпендикулярные

координатные прямые x, y, z, пересекающиеся в одной точке 0, соответствующей началу координат каждой оси.

Пунктиром показаны отрицательные части осей.

xyz01Ox ⊥ Oy ⊥ OzOx – ось абсциссOy – ось ординатOz – ось аппликатКоординатные оси:Выберем в пространстве

Слайд 5x
y
z
0
1
1
1
Координатные плоскости:
Oxz
Oxy
Oyz

Слайд 6 Координатные плоскости:
xz
⊥
xy
⊥
yz

Слайд 7Положение любой точки в пространстве определяется тремя координатами . Проследим

как их получить: 1) проведем перпендикуляр из точки A к плоскости

Oxy , обозначив точку пересечения Axy ( или Axy – ортогональная проекция точки A на плоскость Oxy ) ;

Axy

Положение любой точки в пространстве определяется тремя координатами . Проследим как их получить: 1) проведем перпендикуляр из

Слайд 8x
y
1
1
A
Ayz
Axz
Axy
Ax
Ay

z
1
2) Далее, в плоскости Oxy, из точки Axy опустим перпендикуляры

на координатные оси этой плоскости;
3) Построим прямую пересечения AxAxz плоскостей

Оxz и (AAxуAx) – по свойству она параллельна AAху; аналогично, Оуz  (AAxуAу)= AyAyz;

xy11AAyzAxzAxyAxAyz12) Далее, в плоскости Oxy, из точки Axy опустим перпендикуляры на координатные оси этой плоскости;3) Построим прямую

Слайд 9x
y
1
1
A
Ayz
Axz
Axy
Ax
Ay

z
1
4) Таким образом, мы получили ортогональные проекции точки A на

координатные плоскости – точки Axz и Ayz;
5) Осталось опустить перпендикуляры

из точек Ayz и Axz на координатную ось аппликат;

xy11AAyzAxzAxyAxAyz14) Таким образом, мы получили ортогональные проекции точки A на координатные плоскости – точки Axz и Ayz;5)

Слайд 10x
y
0
1
1
1
A
Ayz
Axz
Axy
Ax
Az
Ay

z
Тогда, AAx ⊥ Ox, AAy ⊥ Oy и AAz ⊥

Oz (объясните почему?). Числа a; b; c, соответствующие координатам точек

Ax, Ay и Az на числовых осях и являются координатами точки A. Записывают : A(a; b; c). Очевидно, что начало координат в пространстве O(0; 0; 0).

xy0111AAyzAxzAxyAxAzAyzТогда, AAx ⊥ Ox, AAy ⊥ Oy и AAz ⊥ Oz (объясните почему?). Числа a; b; c,

Слайд 11x
y
0
1
1
1
A
Ayz
Axz
Axy
Ax
Az
Ay

z
Координаты точки можно понимать как линейные размеры |a| × |b|

× |c| прямоугольного параллелепипеда (если координата отрицательная, то берется модуль

числа), а положение точки – противоположная началу координат вершина получающегося прямоугольного параллелепипеда. Т.е. модуль каждой координаты равен расстоянию от данной точки до одной из координатных плоскостей.

|a|

|b|

|c|

xy0111AAyzAxzAxyAxAzAyzКоординаты точки можно понимать как линейные размеры |a| × |b| × |c| прямоугольного параллелепипеда (если координата отрицательная,

Слайд 121
x
y
z
0
1
1

2
3
2
Пример 1. Изобразить точки A(1; 2; 3), B(−2; 2; 1)

и C(2; −2; − 3).
A(1; 2; 3)
Для изображения точки A

построим ломанную, состоящую из трех последовательных звеньев. От начала координат откладываем 1 ед.отр. вдоль оси Ox. Затем второе звено длиной 2 ед.отр. параллельно оси Oy. И последний отрезок длиной 3 ед.отр. параллельно оси Oz.

1xyz011232Пример 1. Изобразить точки A(1; 2; 3), B(−2; 2; 1) и C(2; −2; − 3).A(1; 2; 3)Для

Слайд 13x
y
z
0
1
1
A
1
2
3
2
A(1; 2; 3)

B
−2
B(−2; 2; 1)
C(2; −2; − 3)
C
−2
2
−3

Проследите и самостоятельно

сформулируйте построение точек B и C.

Слайд 141). Если одна из координат точки равна 0, то точка

лежит в одной из координатных плоскостей; (например, M∈Oyz, N∈Oxz, K∈Oxy).
x
y
z
0
1
1
1
Отметим

некоторые свойства координат точек:

2). Если две координаты точки равны 0, то точка принадлежит одной из координатных осей; (например, P∈Ox, S∈Oy, R∈Oz).

−2

M(0; −2; 3)

N(−2; 0; 1)

K(1; 3; 0)

−2

P(2; 0; 0)

R(0; 0; −2)

S(0; 2; 0)

1). Если одна из координат точки равна 0, то точка лежит в одной из координатных плоскостей; (например,

Слайд 15x
y
z
0
1
1
A
1

a
b
c
Пусть A(a; b; c)
−a
−b
−c
A0

Построим точку A0, симметричную данной точке относительно

точки O.
3). Тогда координаты точки A0(−a; −b; −c).

Центральная симметрия

xyz011A1abcПусть A(a; b; c)−a−b−cA0Построим точку A0, симметричную данной точке относительно точки O.3). Тогда координаты точки A0(−a; −b;

Слайд 16x
y
z
0
1
1
A
1
a
b
c
Пусть A(a; b; c)
−c
−b

A1
Построим точку A1, симметричную данной точке относительно

оси Ox.
4). Тогда координаты точки A1(a; −b; −c).

Осевая симметрия

xyz011A1abcПусть A(a; b; c)−c−bA1Построим точку A1, симметричную данной точке относительно оси Ox.4). Тогда координаты точки A1(a; −b;

Слайд 17x
y
z
0
1
1
A
1
a
b
c
Пусть A(a; b; c)
−c
−a

A2
Построим точку A2, симметричную данной точке относительно

оси Oy.
5). Тогда координаты точки A2(−a; b; −c).

Осевая симметрия

xyz011A1abcПусть A(a; b; c)−c−aA2Построим точку A2, симметричную данной точке относительно оси Oy.5). Тогда координаты точки A2(−a; b;

Слайд 18x
y
z
0
1
1
A
1
a
b
c
Пусть A(a; b; c)
−a
−b

A3
Построим точку A3, симметричную данной точке относительно

оси Oz.
6). Тогда координаты точки A3(−a; −b; c).

Осевая симметрия

xyz011A1abcПусть A(a; b; c)−a−bA3Построим точку A3, симметричную данной точке относительно оси Oz.6). Тогда координаты точки A3(−a; −b;

Слайд 19x
y
z
0
1
1
A
1
a
b
c
Пусть A(a; b; c)
−c

A4
Построим точку A4, симметричную данной точке относительно

плоскости Oxy.
7). Тогда координаты точки A4(a; b; −c).

Зеркальная симметрия

xyz011A1abcПусть A(a; b; c)−cA4Построим точку A4, симметричную данной точке относительно плоскости Oxy.7). Тогда координаты точки A4(a; b;

Слайд 20x
y
z
0
1
1
A
1
a
b
c
Пусть A(a; b; c)
−b

A5
Построим точку A5, симметричную данной точке относительно

плоскости Oxz.
8). Тогда координаты точки A5(a; −b; c).

Зеркальная симметрия

xyz011A1abcПусть A(a; b; c)−bA5Построим точку A5, симметричную данной точке относительно плоскости Oxz.8). Тогда координаты точки A5(a; −b;

Слайд 21x
y
z
0
1
1
A
1
a
b
c
Пусть A(a; b; c)

A6
9). Тогда координаты точки A6(−a; b; c).

Зеркальная

симметрия
Построим точку A6, симметричную данной точке относительно плоскости Oyz.

−a

xyz011A1abcПусть A(a; b; c)A69). Тогда координаты точки A6(−a; b; c).Зеркальная симметрияПостроим точку A6, симметричную данной точке относительно

Слайд 22
x
y
0
1
1
A
z
1
Расстояние между точками A(x1; y1; z1) и B(x2; y2; z2)
B

x1
x2

y1
y2
z1
z2
|x1–x2|
|y1–y2|
|z1–z2|

C

Слайд 23x
y
0
1
1
A
z
1
Координаты середины отрезка АВ, где A(x1; y1; z1) и B(x2;

y2; z2)
B
x1
x2

y1
y2
z1
z2

M

Скачать презентацию

Теги

Разделы презентаций

Система координат в пространстве

Содержание

Слайды и текст этой презентации

Слайд 1Геометрия, 11 классСистема координат в пространствеВоробьев Леонид Альбертович, г.Минск

Слайд 2Вспомним, как определяется координатная(числовая) прямая.Изображаем произвольную прямую;х01МаТогда любой точке этой

координатной прямой соответствует единственное действительной число a. И наоборот, любое

Слайд 3А теперь, что мы подразумеваем под координатной плоскостью.ух011МаbM(a; b)

Слайд 4xyz01Ox ⊥ Oy ⊥ OzOx – ось абсциссOy – ось

ординатOz – ось аппликатКоординатные оси:Выберем в пространстве три попарно перпендикулярные

Слайд 5xyz0111 Координатные плоскости:OxzOxyOyz

Слайд 6 Координатные плоскости:xz⊥xy⊥yz

Слайд 7Положение любой точки в пространстве определяется тремя координатами . Проследим

как их получить: 1) проведем перпендикуляр из точки A к плоскости

Слайд 8xy11AAyzAxzAxyAxAyz12) Далее, в плоскости Oxy, из точки Axy опустим перпендикуляры

на координатные оси этой плоскости;3) Построим прямую пересечения AxAxz плоскостей

Слайд 9xy11AAyzAxzAxyAxAyz14) Таким образом, мы получили ортогональные проекции точки A на

координатные плоскости – точки Axz и Ayz;5) Осталось опустить перпендикуляры

Слайд 10xy0111AAyzAxzAxyAxAzAyzТогда, AAx ⊥ Ox, AAy ⊥ Oy и AAz ⊥

Oz (объясните почему?). Числа a; b; c, соответствующие координатам точек

Слайд 11xy0111AAyzAxzAxyAxAzAyzКоординаты точки можно понимать как линейные размеры |a| × |b|

× |c| прямоугольного параллелепипеда (если координата отрицательная, то берется модуль

Слайд 121xyz011232Пример 1. Изобразить точки A(1; 2; 3), B(−2; 2; 1)

и C(2; −2; − 3).A(1; 2; 3)Для изображения точки A

Слайд 13xyz011A1232A(1; 2; 3)B−2B(−2; 2; 1)C(2; −2; − 3)C−22−3Проследите и самостоятельно

сформулируйте построение точек B и C.

Слайд 141). Если одна из координат точки равна 0, то точка

лежит в одной из координатных плоскостей; (например, M∈Oyz, N∈Oxz, K∈Oxy).xyz0111Отметим

Слайд 15xyz011A1abcПусть A(a; b; c)−a−b−cA0Построим точку A0, симметричную данной точке относительно

точки O.3). Тогда координаты точки A0(−a; −b; −c).Центральная симметрия

Слайд 16xyz011A1abcПусть A(a; b; c)−c−bA1Построим точку A1, симметричную данной точке относительно

оси Ox.4). Тогда координаты точки A1(a; −b; −c).Осевая симметрия

Слайд 17xyz011A1abcПусть A(a; b; c)−c−aA2Построим точку A2, симметричную данной точке относительно

оси Oy.5). Тогда координаты точки A2(−a; b; −c).Осевая симметрия

Слайд 18xyz011A1abcПусть A(a; b; c)−a−bA3Построим точку A3, симметричную данной точке относительно

оси Oz.6). Тогда координаты точки A3(−a; −b; c).Осевая симметрия

Слайд 19xyz011A1abcПусть A(a; b; c)−cA4Построим точку A4, симметричную данной точке относительно

плоскости Oxy.7). Тогда координаты точки A4(a; b; −c).Зеркальная симметрия

Слайд 20xyz011A1abcПусть A(a; b; c)−bA5Построим точку A5, симметричную данной точке относительно

плоскости Oxz.8). Тогда координаты точки A5(a; −b; c).Зеркальная симметрия

Слайд 21xyz011A1abcПусть A(a; b; c)A69). Тогда координаты точки A6(−a; b; c).Зеркальная

симметрияПостроим точку A6, симметричную данной точке относительно плоскости Oyz.−a

Слайд 22xy011Az1Расстояние между точками A(x1; y1; z1) и B(x2; y2; z2)Bx1x2y1y2z1z2|x1–x2||y1–y2||z1–z2|C

Слайд 23xy011Az1Координаты середины отрезка АВ, где A(x1; y1; z1) и B(x2;

y2; z2)Bx1x2y1y2z1z2M

Похожие презентации

Обратная связь

Что такое TheSlide.ru?