Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Составление модели для вычислений экономических задач на кредиты
Содержание
- 1. Составление модели для вычислений экономических задач на кредиты
- 2. 25 января 2020 года Сарыал собирается взять
- 3. 105S1 80000 100 80000
- 4. 2) 31 декабря 2013 года Сергей взял
- 5. 3) В июле 2016 года планируется взять
- 6. 4) В июле 2016 года планируется взять
- 7. 5) 15-го января планируется взять кредит в
- 8. 6) В июле планируется взять кредит в
- 9. n n n n1Найдем выплаты:x 9 1,1 9(n 1)
- 10. ((a(a+в)2=a2+2aв+в2-в)2=a2-2aв+в2a2-в2=(a-в) a+в)(a+в)3=a3+3a2в+3aв2+в3Спасибо завнимание!Я сдамГИА
- 11. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1a2
(a+в)
(a-
(a+
(a+
в)3=a3+3a2в+3aв2+в3
в)2=a2+2aв+в2 в)2=a2-2aв+в2
-в2=(a-в)
Составление модели для вычислений экономических задач
на кредУчиитетльыматематики
МОБУ «СОШ №17»
г.Якутска
Егоров
Алексей Александрович
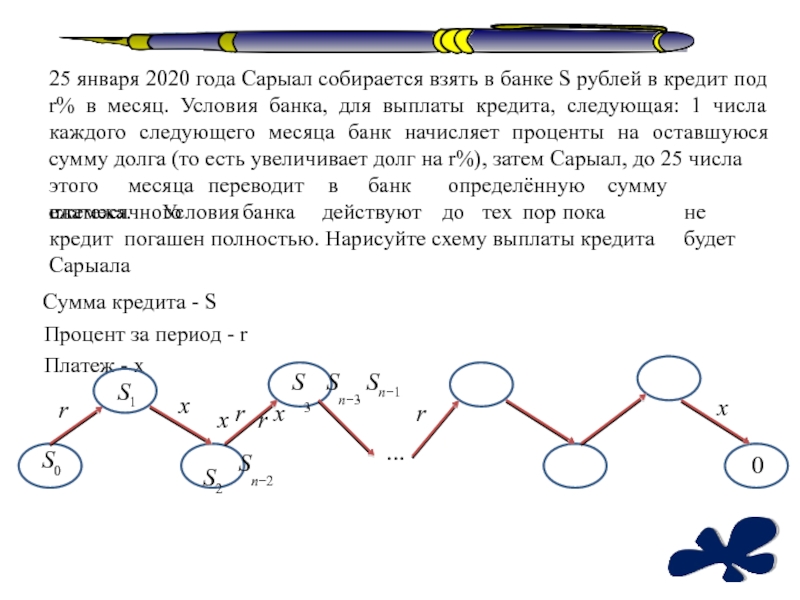
Слайд 225 января 2020 года Сарыал собирается взять в банке S
рублей в кредит под r% в месяц. Условия банка, для
выплаты кредита, следующая: 1 числа каждого следующего месяца банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на r%), затем Сарыал, до 25 числаэтого месяца переводит в банк определённую сумму ежемесячного
не будет
платежа. Условия банка действуют до тех пор пока кредит погашен полностью. Нарисуйте схему выплаты кредита Сарыала
Сумма кредита - S Процент за период - r Платеж - х
1
S
...
S2 Sn2
S3 Sn3 Sn1
0
r
S0
r
r x
x x r
x
Слайд 3105
S1 80000 100 80000 1,05 84000
руб.
1) В начале года некоторую сумму денег S вложили в банк
на r% годовых. Определите сумму вклада через один год, если S=80000 рублей, а r= 5%.а) Вклад увеличился на 100 + 5 = 105%.
Найдем 105% :
k =1 + 0,01r
80000100%.
S1 105%.
Увеличили на 15%:
Увеличили на 20%:
Увеличили на 37%:
S1 80000 1,15 S1 80000 1,2 S1 80000 1,37
Слайд 42) 31 декабря 2013 года Сергей взял в банке 9
930 000 рублей в кредит под 10% годовых. Схема выплаты
кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (тоесть увеличивает долг на 10%), затем Сергей переводит в
банк определённую сумму ежегодного платежа. Какой должна быть сумма
ежегодного платежа, чтобы Сергей выплатил долг тремя равными ежегодными платежами?
S 9930000 руб r 10%
х – ежегодная выплата
k = 1 + 0,01· 10 = 1,1
Составим модель задачи
((99300001,1 х) 1,1 х) 1,1 х 0
Слайд 53) В июле 2016 года планируется взять кредит в банке
на три года в размере S млн рублей, где S
— целое число. Условия его возврата таковы:каждый январь долг увеличивается на 25% по сравнению с концом предыдущего года;
с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;
в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей
Найдите наименьшее S, при котором каждая из выплат будет больше 5 млн рублей.
r = 25% k =1 + 0,01r = 1 + 0,01· 25 = 1,25
0,475S 5
Слайд 64) В июле 2016 года планируется взять кредит в банке
на пять лет в размере S тыс рублей. Условия его
возврата таковы:каждый январь долг возрастает на 20% по сравнению с концом предыдущего года;
с февраля по июнь каждого года необходимо выплатить часть долга;
в июле 2017,2018 и 2019 долг остаётся равным S тыс. рублей;
выплаты в 2020 и 2021 годах равны по 360 тыс. рублей;
к июлю 2021 долг будет выплачен полностью. Найдите общую сумму выплат за пять лет.
r = 20% k =1 + 0,01r = 1 + 0,01· 20 = 1,2
(1,2S – 360) · 1,2 – 360 = 0
Sn 3 0,2S 2 360
Слайд 75) 15-го января планируется взять кредит в банке на девять
месяцев. Условия его возврата таковы:
1-го числа каждого месяца долг возрастает
на r% по сравнению с концом предыдущего месяца;со 2-го по 14-е число месяца необходимо выплатить часть долга;
15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.
Известно, что общая сумма выплат после полного погашения кредита на 25% больше суммы,
взятой в кредит. Найдите r.
k =1 + 0,01r
Кредит взят на 9 месяцев и каждый месяц на одну и ту же сумму меньше, тогда:
9 9 9 9 9 9 9 9
n
S 8S 7S 6S 5S 4S 3S 2S S 4S
9
9 9
9
9
9
9
8Sk 7Sk 6Sk 5Sk 4Sk 3Sk 2Sk Sk
Sk n Sk
9 5Sk
5Sk 4S 1,25S
Слайд 86) В июле планируется взять кредит в банке на сумму
9 млн рублей на некоторый срок (целое число лет). Условия
его возврата таковы:каждый январь долг возрастает на 10% по сравнению с концом предыдущего года;
с февраля по июнь каждого года необходимо выплатить часть долга;
в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
Чему будет равна общая сумма выплат после полного погашения кредита, если наибольший годовой платеж составит 1,5 млн рублей?
r = 10% k =1 + 0,01r = 1 + 0,01· 10 = 1,1
Пусть кредит планируется взять на n лет, тогда:
Sn x1 x2 x3 ... xn2 xn1 xn
Слайд 9n n n n
1
Найдем выплаты:
x 9 1,1 9(n 1) 9,9n
9n 9 0,9n 9 0,9
9n n n n n
2
x 9(n 1) 1,1 9 n 2 9,9n 9,9 9n 18 0,9n 8,1 0,9 8,1
n n n n n
3
x 9(n 2) 1,1 9 n 3 9,9n 19,8 9n 27 0,9n 7,2 0,9 7,2
.......................................
Начиная со второй суммы выплат уменьшаются, значит наибольшая выплата равна х1:
0,9 9 1,5
n n
9
0,6 0,6n 9
0,9 0,9
n
15 0,06млн. руб.
2
S 2 1,5 14 0,06 15 16,2млн. руб.
Выплаты начиная со второго уменьшаются на одну и ту же сумму:
Используя формулу суммы арифметической прогрессии найдем общую сумму выплат:
n 15 (количество лет)
Ответ :16,2млн. руб.