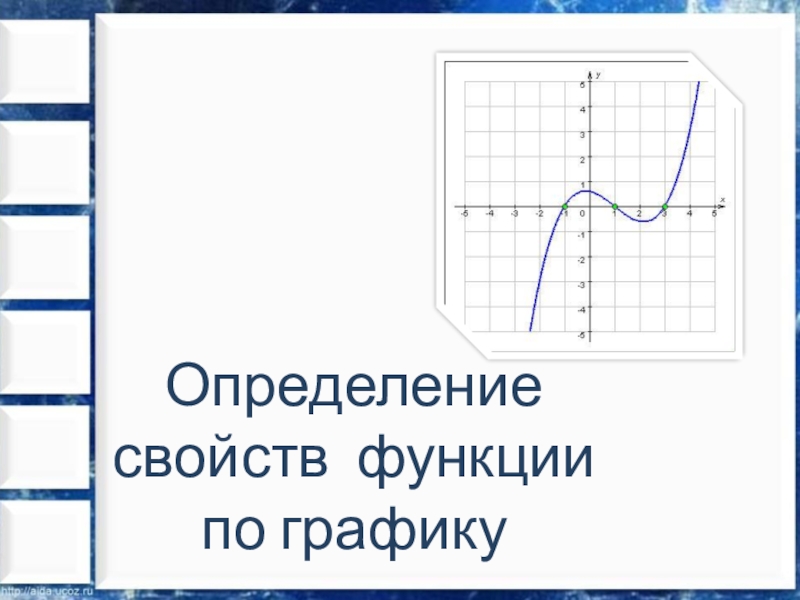
Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Свойства параллельных плоскостей 5 класс
Содержание
- 1. Свойства параллельных плоскостей 5 класс
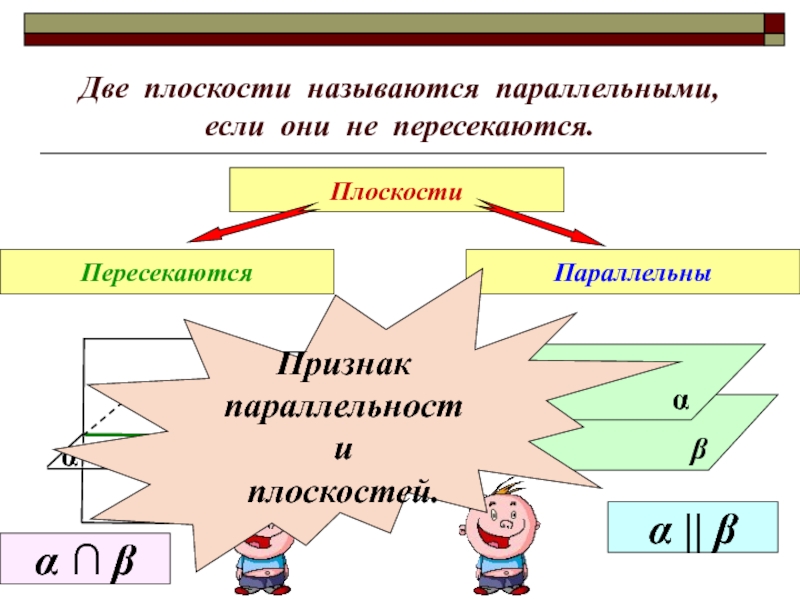
- 2. Две плоскости называются параллельными, если они не пересекаются.ПлоскостиПересекаютсяПараллельныβαα || β α ∩ β Признак параллельностиплоскостей.
- 3. Карточка №1 Построить и проанализировать эскизы
- 4. Ответы к карточке №1 Построить и
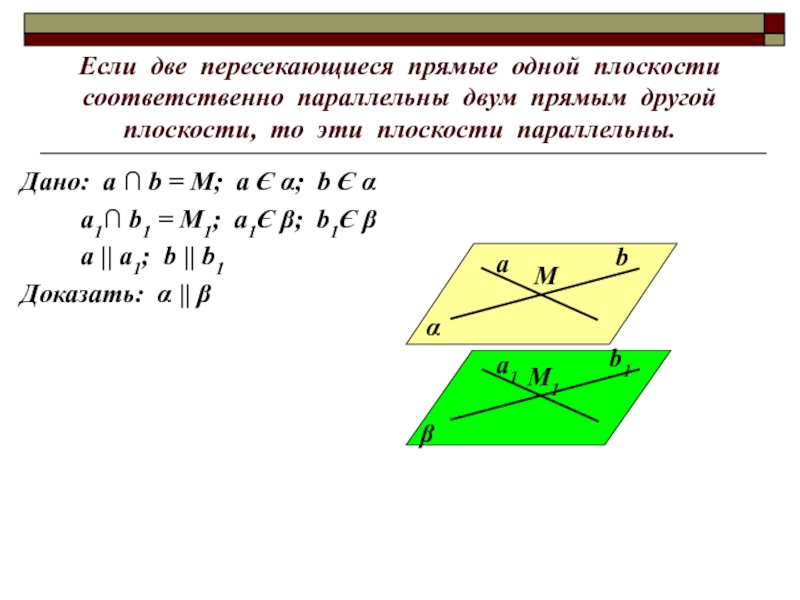
- 5. Если две пересекающиеся прямые одной плоскости соответственно
- 6. Если две пересекающиеся прямые одной плоскости соответственно
- 7. ТЕОРЕМА: Если две параллельные плоскости пересекаются третьей,
- 8. Отрезки параллельных прямых, заключённые между двумя параллельными плоскостями, равны.аВ1bА1А2В2 а2 а1
- 9. Тест Ответьте на вопросы:Могут ли прямая
- 10. Геометрический диктантДве прямые в пространстве называются ПАРАЛЛЕЛЬНЫМИ….________________________________________________________Через
- 11. Ответы к геометрическому диктанту Две прямые
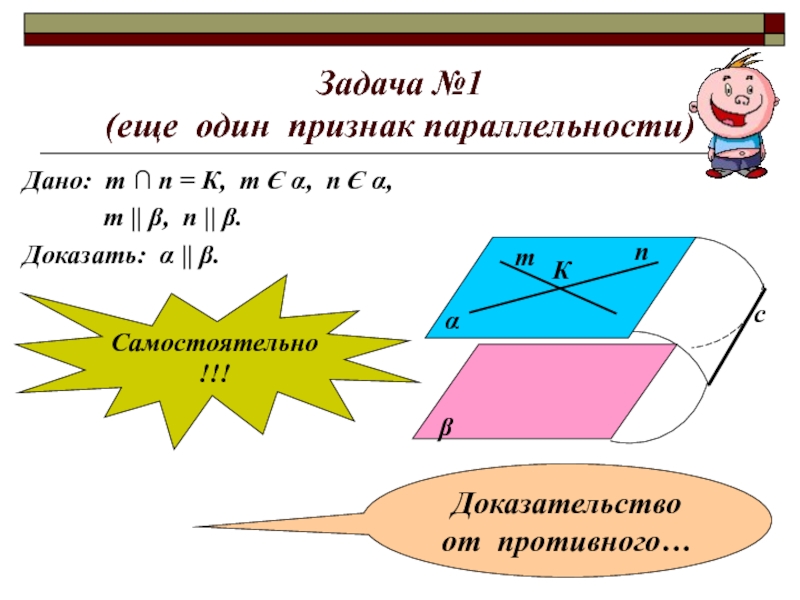
- 12. Задача №1 (еще один признак параллельности)Дано: т
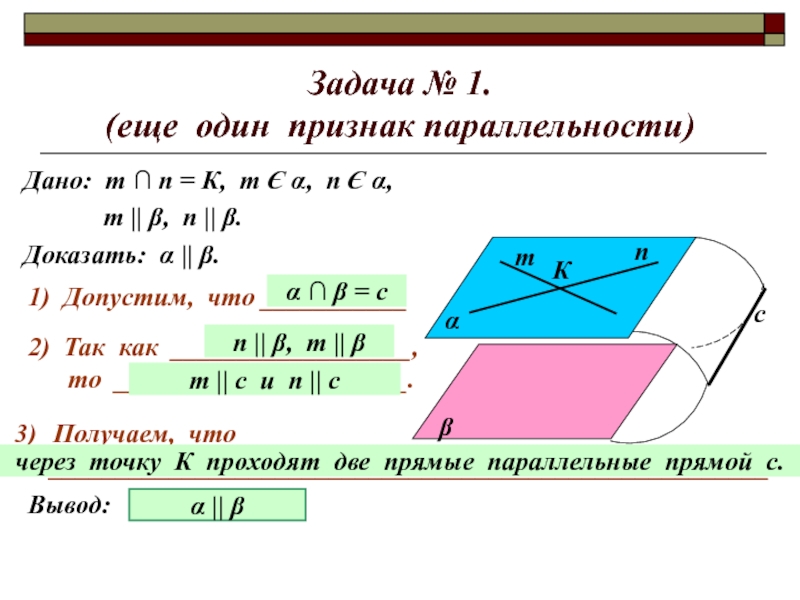
- 13. Задача № 1. (еще один признак параллельности)Дано:
- 14. Задача № 2Дано: отрезки А1А2; В1В2; С1С2О
- 15. Задача № 2Дано: отрезки А1А2; В1В2; С1С2О
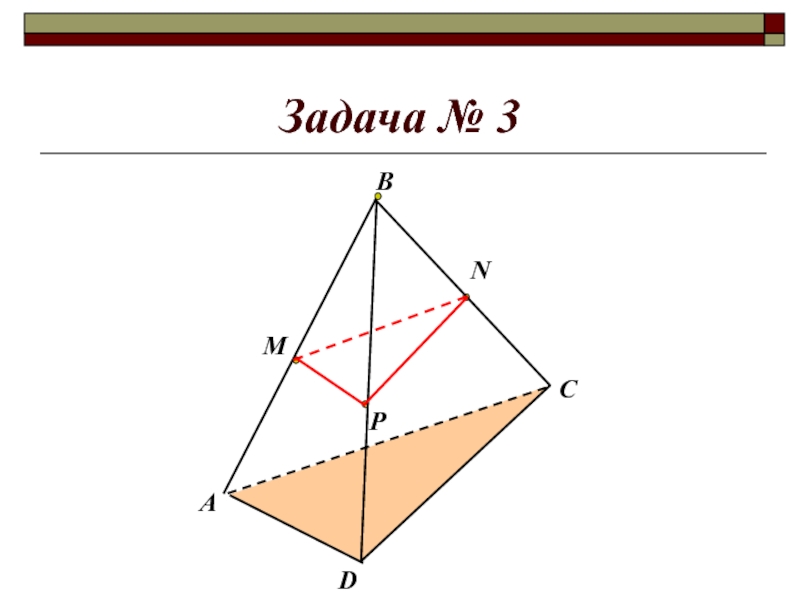
- 16. Задача № 3МРNАВ DC
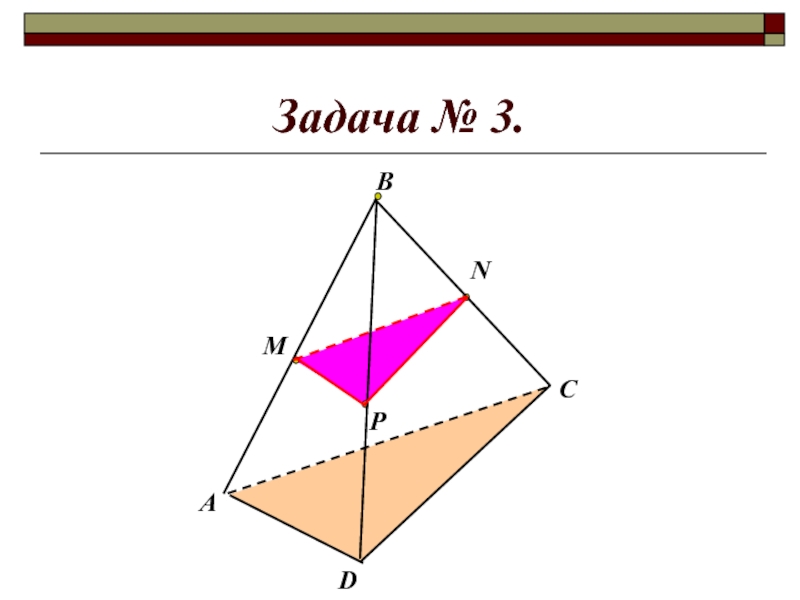
- 17. Задача № 3.МРNА DCВ
- 18. Домашнее задание:П. 10, №№ 29,30Удачи!
- 19. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Тема: «Свойства параллельных плоскостей».
ЦЕЛЬ:
Познакомить уч-ся со свойствами параллельных плоскостей; повторить
Слайд 2Две плоскости называются параллельными, если они не пересекаются.
Плоскости
Пересекаются
Параллельны
β
α
α || β
α ∩ β
Признак
параллельности
плоскостей.
Слайд 3Карточка №1 Построить и проанализировать эскизы чертежей к возможным трём
случаям взаимного расположения прямой и плоскости в пространстве: Прямая лежит в
плоскости. Прямая и плоскость имеют только одну точку. 3.Прямая и плоскость не имеют общих точек.Слайд 4Ответы к карточке №1 Построить и проанализировать эскизы чертежей к
возможным трём случаям взаимного расположения прямой и плоскости в пространстве: Прямая
лежит в плоскости. Прямая и плоскость имеют только одну точку. 3.Прямая и плоскость не имеют общих точек.Слайд 5Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым
другой плоскости, то эти плоскости параллельны.
Дано: а ∩ b
= М; а Є α; b Є α а1∩ b1 = М1; а1Є β; b1Є β
a || a1; b || b1
Доказать: α || β
α
β
а
b
М
b1
а1
М1
Слайд 6Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым
другой плоскости, то эти плоскости параллельны.
Доказательство: (от противного)
Пусть
α ∩ β = сТогда а || β, т.к. a || a1, а1 Є β
а Є α; α ∩ β = с, значит а || с.
b || β, т.к. b || b1, b1 Є β
b Є α α ∩ β = с, значит b || с.
Имеем а || b, то есть
через точку М проходят
две прямые а и b,
параллельные прямой с.
Получили противоречие. Значит, α || β .
α
β
а
b
М
b1
а1
М1
с
По признаку параллельности прямой и плоскости а || β и b || β.
Слайд 7ТЕОРЕМА: Если две параллельные плоскости пересекаются третьей, то прямые пересечения
параллельны.
ДОК-ВО: Согласно определению параллельные прямые- это прямые ,которые лежат в
одной плоскости – секущей плоскости. Они не пересекаются ,так как не пересекаются содержащие их параллельные плоскости. Значит, прямые параллельны. Теорема доказана.Сообщение нового материала
Свойства параллельных плоскостей.
Слайд 8Отрезки параллельных прямых, заключённые между двумя параллельными плоскостями, равны.
а
В1
b
А1
А2
В2
а2
а1
Слайд 9Тест
Ответьте на вопросы:
Могут ли прямая и плоскость не иметь
общих точек?
Верно ли, что если две прямые не пересекаются, то
они параллельны?Плоскости α и β параллельны, прямая т лежит в плоскости α. Верно ли, что прямая т параллельна плоскости β?
Верно ли, что если прямая а параллельна одной из двух параллельных плоскостей, с другой плоскостью прямая а имеет одну общую точку?
Верно ли, что плоскости параллельны, если прямая, лежащая в одной плоскости, параллельна другой плоскости?
Да
Нет
Да
Нет
Нет
Слайд 10Геометрический диктант
Две прямые в пространстве называются ПАРАЛЛЕЛЬНЫМИ….
________________________________________________________
Через точку вне данной
прямой можно провести прямую, параллельную этой прямой ,и ____________________________.
Две прямые,
параллельные третьей прямой, __________________.Две плоскости параллельны, если одна из них параллельна двум пересекающимся прямым, лежащим _________________________
Если две прямые параллельны третьей прямой, то они _________________________________________________________
Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая _________________________________________
Слайд 11Ответы к геометрическому диктанту Две прямые в пространстве называются ПАРАЛЛЕЛЬНЫМИ ,если
они лежат в одной плоскости и не пересекаются. Через точку вне
данной прямой можно провести прямую, параллельную этой прямой ,и притом только одну. Две прямые, параллельные третьей прямой, параллельны Две плоскости параллельны, если одна из них параллельна двум пересекающимся прямым, лежащим в другой плоскости Если две прямые параллельны третьей прямой, то они параллельны Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскостьСлайд 12Задача №1
(еще один признак параллельности)
Дано: т ∩ п = К,
т Є α, п Є α,
т || β, п || β.Доказать: α || β.
Самостоятельно!!!
Доказательство
от противного…
Слайд 13Задача № 1.
(еще один признак параллельности)
Дано: т ∩ п =
К, т Є α, п Є α,
т || β, п || β.Доказать: α || β.
1) Допустим, что ___________
2) Так как __________________,
то ______________________.
Получаем, что
______________________________________________________.
Вывод:
α ∩ β = с
п || β, т || β
т || с и п || с
через точку К проходят две прямые параллельные прямой с.
α || β
Слайд 14Задача № 2
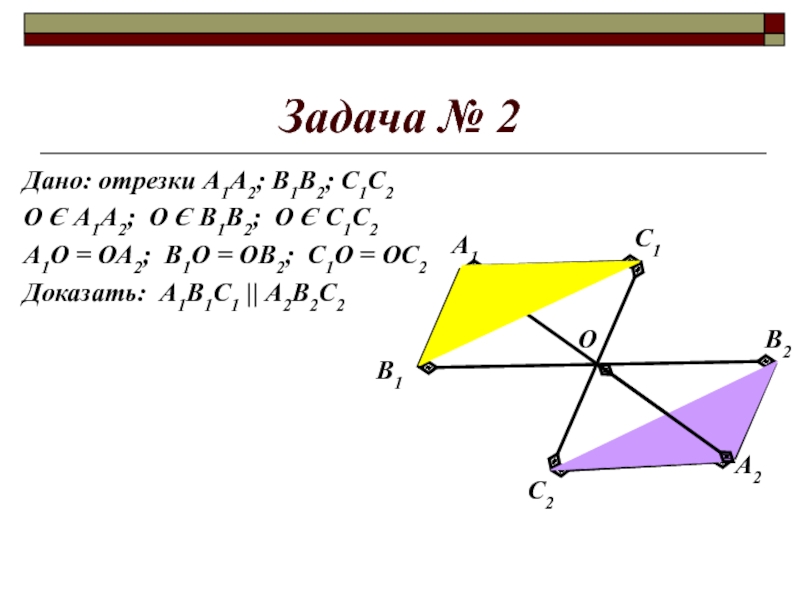
Дано: отрезки А1А2; В1В2; С1С2
О Є А1А2; О
Є В1В2; О Є С1С2
А1О = ОА2; В1О = ОВ2;
С1О = ОС2Доказать: А1В1С1 || А2В2С2
А1
В1
А2
В2
С2
С1
О
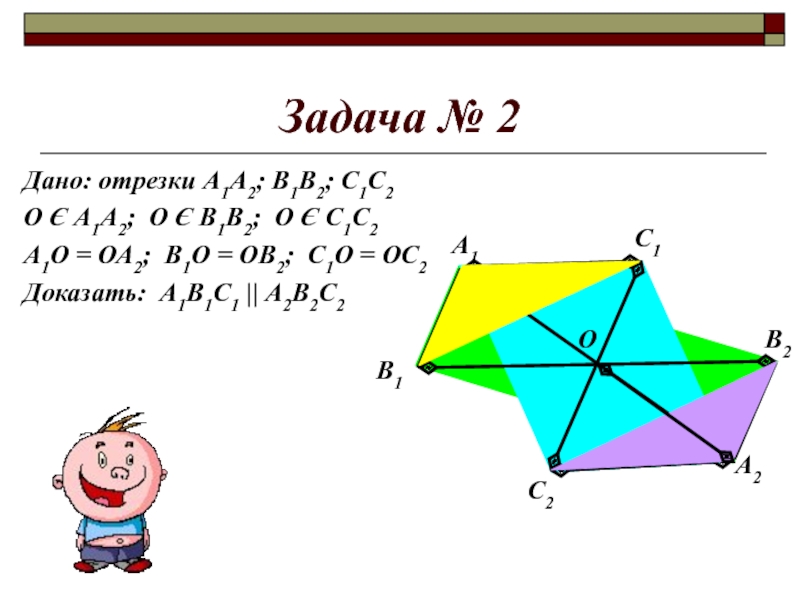
Слайд 15Задача № 2
Дано: отрезки А1А2; В1В2; С1С2
О Є А1А2; О
Є В1В2; О Є С1С2
А1О = ОА2; В1О = ОВ2;
С1О = ОС2Доказать: А1В1С1 || А2В2С2
В2
С1
А1
В1
А2
С2
О