Слайд 2Тайны чисел
Выполнили: Каримова А.
Шевелева И.
Проверила уч. математики:
Степанова Н. Ю.
Слайд 3Комплексные числа.
Это числа вида a + bi, где а и
b-действительные числа, а i -число особого рода, квадрат которого =
–1,т.е. i² =–1.
Действия над комплексными числами выполняются по таким же правилам, что и над многочленами, при этом i² заменяют на –1. Например:
( 2+3 i) + (4–8 i)= 6–5 i;
( 2+3 i)· (4–8 i)= 8–16 i+12 i–24 i²=32–4 i.
Слайд 4Числа Фибоначчи
Имя Леонардо Фибоначчи–крупного итальянского математика, автора
«Книги об абаке» (1202), которая несколько веков оставалась основным хранилищем
сведений по арифметике и алгебре, сейчас встречается чаще всего в связи с замечательной числовой последовательностью 1,2,3,5,8,13,21,34,55,89,… .
Ее члены называются числами Фибоначчи.
Слайд 5Среднее арифметическое
Средним арифметическим п положительных
чисел а ,а , …,а называется число
m =
.
Среднее
геометрическое
Среднем геометрическим п положительных чисел а ,а ,…а называется корень п-й степени из проведения этих
чисел:
g=
.
Слайд 6Среднее гармоническое
Средним гармоническим п положительных чисел а ,а …а называется
число
h=
Среднее квадратичное
Среднем квадратичным п произвольных чисел а , а …а
называется число
d=
Слайд 7Для любых положительных чисел а , а ,… а эти
средние удовлетворяют неравенствам:h g m d,в каждом
из которых знак равенства достигается лишь в случае , когда а = а = …= а ,
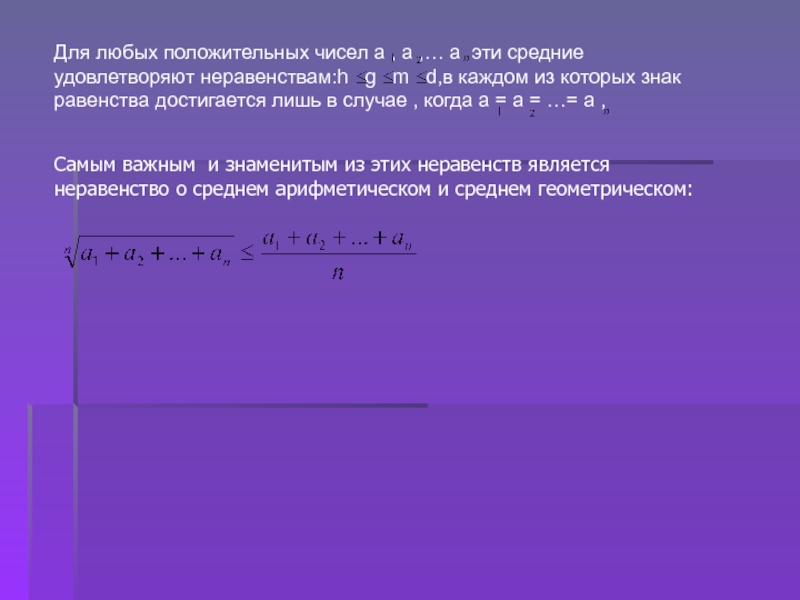
Самым важным и знаменитым из этих неравенств является неравенство о среднем арифметическом и среднем геометрическом:
Фигурные числа.
Простейшими из них являются треугольные числа:1,3,6,10,15,21, 28,36…
Отсюда видно, что последовательность треугольных чисел можно легко составить следующим образом: из ряда натуральных чисел 1,1,2,3,4,5,6,7,8,9.10,11.12… берём первое число 1, затем сумму первых двух (1+2=3),сумму первых трёх(1+2+3=6), четырёх(1+2+3+4=10) чисел и т.д.
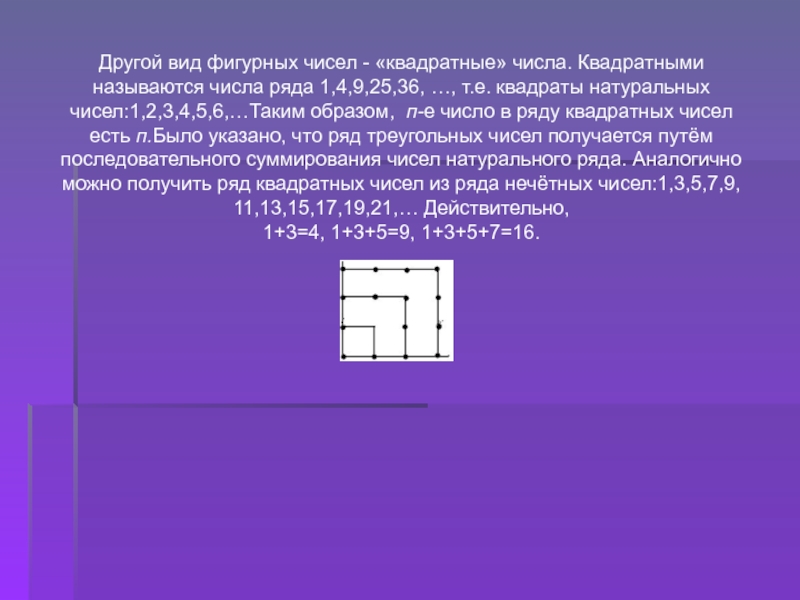
Слайд 9Другой вид фигурных чисел - «квадратные» числа. Квадратными называются числа
ряда 1,4,9,25,36, …, т.е. квадраты натуральных чисел:1,2,3,4,5,6,…Таким образом, п-е число
в ряду квадратных чисел есть п.Было указано, что ряд треугольных чисел получается путём последовательного суммирования чисел натурального ряда. Аналогично можно получить ряд квадратных чисел из ряда нечётных чисел:1,3,5,7,9, 11,13,15,17,19,21,… Действительно,
1+3=4, 1+3+5=9, 1+3+5+7=16.
Слайд 10 «Совершенные» числа.
Это числа, которые
в точности равны сумме своих делителей, например число 6.Его собственные
делители – 1,2,3.Имеем: 6=1+2+3. Пифагорейцы считали замечательными числами все числа, обладающие таким свойством, поэтому их называли «совершенными». Они знали только три таких числа:6,28,496.
28=1+2+4+7+14;
496=1+2+4+8+16+31+62+124+248.
В «Арифметике» Никомаха из Геразы(1 в. н. э.) имеется четвёртое совершенное число:8128.Никомах писал:«Совершенные» числа красивы. Однако красивые вещи редки и малочисленны. Большинство чисел являются избыточными или недостаточными, в то время как совершенных чисел немного. Среди единиц их всего лишь одно, так же среди десятков, сотен и тысяч».
Пятое совершенное число 2 (2 - 1)=33 550 336
Слайд 11В одной из египетских пирамид ученые обнаружили на каменной плите
гробницы выгравированное иероглифами число 2520. Трудно сказать, за что выпала
такая честь этому числу. Может быть за то, что оно без остатка делится на все без исключения целые числа от 1 до 10. Действительно, нет числа, меньшего, чем 2520, обладающего таким свойством.
Выполнила: ученица 9«А» класса
Александрова Кристина.
Руководитель: Степанова
Нинель Юрьевна.
Тайны функций.
Слайд 13Функция[x]
Для любого действительного числа x символом [x] обозначают
целую часть числа x, т. е наибольшее целое число, не
превосходящее x.
Пример. Вычислим [x], если x принимает значения: 2,3; 0,15; 4; -0,3; -2,5; -5.
Решение. Из определения [x] следует, что [2,3]=2; [0,15]=0; [4]=4; [-0,3]=-1; [-2,5]=-3; [-5]=-5.
Если n-целое число, то [n]= n.
Функцию, ставящую каждому x в соответствие число [x], называют целой частью числа x и обозначают символом [x].Она определена для всех x(-+). Множеством значений этой функции является множество целых чисел. График функции изображен на рисунке. Стрелки означают, что правые концы этих отрезков не принадлежат графику, а левые концы принадлежат - они выделены жирными точками.
Слайд 14Функция{x}
Для любого действительного числа символом {x} обозначают дробную часть числа
x. Если [x]-целая часть числа x ,то полагают:
{x}= x- [x].
Пример. Вычислим {x},если x принимает значения:
5,47; 0,23; 5; -6; -7,29.
Решение. Из определения {x}следует, что
{5,47}= 0,47; {0,23}= 0,23; {5}= 0;{-6}= 0;
{-7,29}= -7,29 - [-7,29] = -7,29+ 8=0,71.
Если n-целое число, то{n}= 0.
Таким образом, имеем функцию, которая ставит в соответствии каждому x(-+) дробную часть этого числа.
Функция {x}определена для всех x(-+), а множество ее значений является промежуток [0;1). Ее график изображен на рисунке.
Слайд 15Функция sgn x
Символом sgn x читается: сигнум икс, обозначает
знак числа x (от латинского слова signum-знак). Этим символом обозначается
и функция, которая каждому числу x(- +) ставит в соответствие число 1, если x>0, число -1, если x<0, и число 0, если x=0, т.е. -
-1, если x<0,
Sgn x = 0, если x=0,
1, если x>0.
Таким образом, функция sgn x определена для всех x(- +).Множество ее значений состоит из трех чисел: -1, 0, 1.
Например:
Sgn (1000) = 1, sgn (-3451) =-1, sgn 0=0.
График функции представлен на рисунке.
Пример: Вычислим sgn (x- 4x+3).
Решение: Функция x- 4x+3 принимает положительные значения при x(-1) (3; +), отрицательные - при x(1; 3) и обращается в нуль при x=1 и x=3.Поэтому
-1, если x(1; 3),
sgn (x- 4x+3)= 0, если x=1 и x=3,
1, если x(-1) (3; +).
Слайд 17«Босоногая» счётная машина
Самой древней и самой простой счётной машиной издавна
являлись пальцы рук и ног.
Слайд 18Абак
С перевода на русский означает «счёты».Более поздними изобретениями для счёта
были бирки с зарубками и верёвки с узелками.
Слайд 19Арифмометр
Первый экземпляр первого в мире арифмометра, выполнявшего все четыре
действия арифметики, был создан 1673 году Г.В.Лейбницем после почти сорокалетней
работы над «арифметическим инструментом».
Слайд 20Электронные машины
Современные ЭВМ по своей структуре очень близки к аналитической
машине Беббиджа, но, в отличие от неё, используют совершенно другой
принцип реализации вычислений, основанный на двоичной системе счисления.
Слайд 21Мир случайного
Выполнили: ученики 9 класса «А»
Приволжской средней школы
Коротков Роман и
Никитин Алексей
Руководитель: Степанова
Нинель Юрьевна
Слайд 22Размещения без повторений
Сколько можно составить телефонных номеров из 6 цифр
каждый, так чтобы все цифры были различны?
Это пример задачи на
размещение без повторений. Размещаются здесь 10 цифр по 6. А варианты, при которых одинаковые цифры стоят в разном порядке считаются разными.
Если X-множество, состоящие из n элементов, m ≤ n, то размещением без повторений из n элементов множества X по m называется упорядоченное множество X, содержащее m элементов.
Количество всех размещений из n элементов по m обозначают
n! - n-факториал (factorial англ.. сомножитель)
- произведение чисел натурального ряда от 1 до какого либо числа n
n!=1*2*3*...*n 0!=1
Значит, ответ на вышепоставленную задачу будет
Слайд 23Перестановки без повторений
В случае n=m (см. размещения без повторений) из
n элементов по m называется перестановкой множества x.
Количество всех перестановок
из n элементов обозначают Pn.
Pn=n!
Действительно при n=m:
Слайд 24Сочетания без повторений
Сочетанием без повторений называется такое размещение, при котором
порядок следования элементов не имеет значения.
Всякое подмножество X состоящее из
m элементов, называется сочетанием из n элементов по m.
Таким образом, количество вариантов при сочетании будет меньше количества размещений.
Число сочетаний из n элементов по m обозначается
Слайд 25Примеры задач
Сколько трехкнопочных комбинаций существует на кодовом замке (все три
кнопки нажимаются одновременно), если на нем всего 10 цифр.
Решение:
Так
как кнопки нажимаются одновременно, то выбор этих трех кнопок – сочетание. Отсюда









![Тайны чисел Функция[x] Для любого действительного числа x символом [x] обозначают целую часть Функция[x] Для любого действительного числа x символом [x] обозначают целую часть числа x, т. е наибольшее целое](/img/thumbs/bb232636ecff4f156222e681b9d2f74b-800x.jpg)
![Тайны чисел Функция{x}Для любого действительного числа символом {x} обозначают дробную часть числа x. Функция{x}Для любого действительного числа символом {x} обозначают дробную часть числа x. Если [x]-целая часть числа x ,то](/img/thumbs/d36a57113043443342a963bf0e36b9a3-800x.jpg)































