Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тела вращения на примере конуса
Содержание
- 1. Тела вращения на примере конуса
- 2. Конус в переводе с греческого «konos» означает
- 3. Большой трактат о конических сечениях был написан
- 4. Понятие конуса Определение: тело, ограниченное конической поверхностью и кругом с границей L, называется конусом.
- 5. боковая (коническая) поверхностьвысота конуса (РО)ось конусавершина конуса (Р)основание конусарадиус конуса (r)Элементы конуса BrобразующиеP
- 6. Прямой круговой конус является объединением всех равных
- 7. Сечение, перпендикулярное к оси конуса
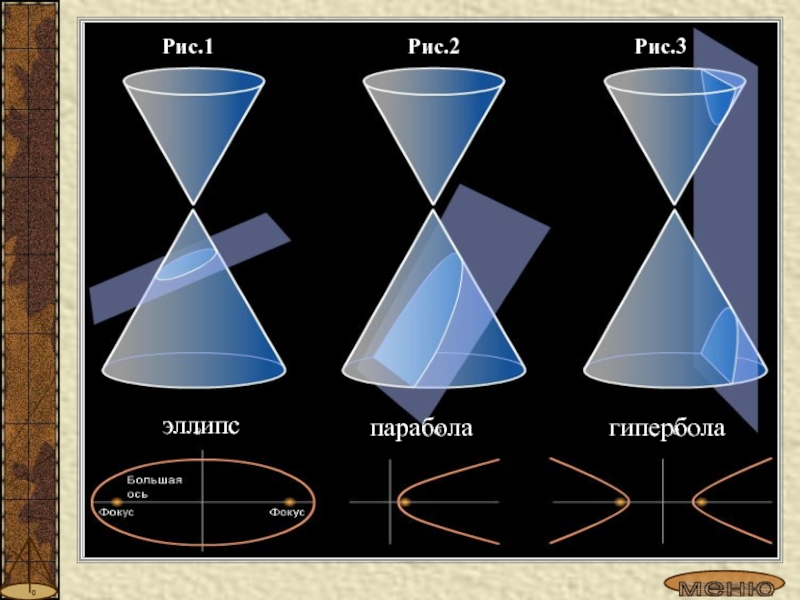
- 8. Рис.1Рис.2Рис.3эллипспараболагипербола
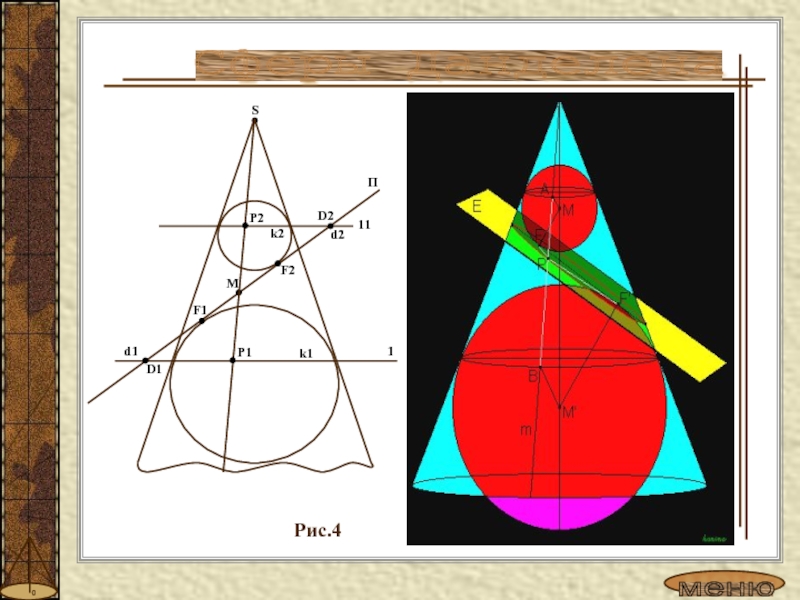
- 9. Рис.4Сферы Данделена
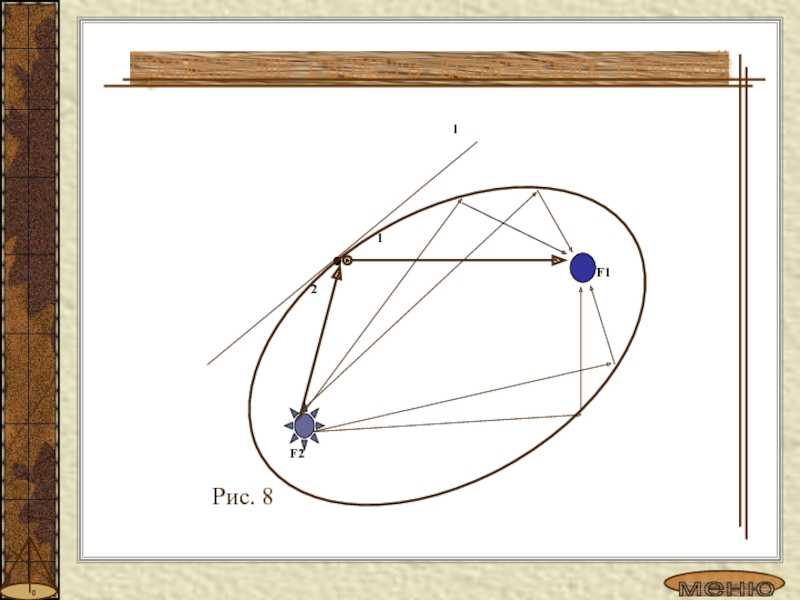
- 10. Применение своиств конических сечений
- 11. За площадь боковой поверхности конуса
- 12. Площадь полной поверхности конуса Площадь
- 13. Усеченным конусом называется пересечение конуса с полупространством,
- 14. Пусть в некоторой плоскости задана какая-нибудь фигура
- 15. Используемые ресурсыhttp://ru.wikipedia.org/wiki/%D0%9A%D0%BE%D0%BD%D1%83%D1%81http://images.yandex.ru/yandsearch?p=0&text=%D0%BA%D0%BE%D0%BD%D1%83%D1%81&img_url=900igr.net%2Fdatai%2Fgeometrija%2FObjom-konusa%2F0001-001-Obem-konusa.jpg&rpt=simage&noreask=1&lr=2
- 16. Скачать презентанцию
Конус в переводе с греческого «konos» означает «сосновая шишка». С конусом люди знакомы с глубокой древности. Много сделала для геометрии школа Платона (428–348 гг. до н. э.). Школе Платона, в частности, принадлежит: а)
Слайды и текст этой презентации
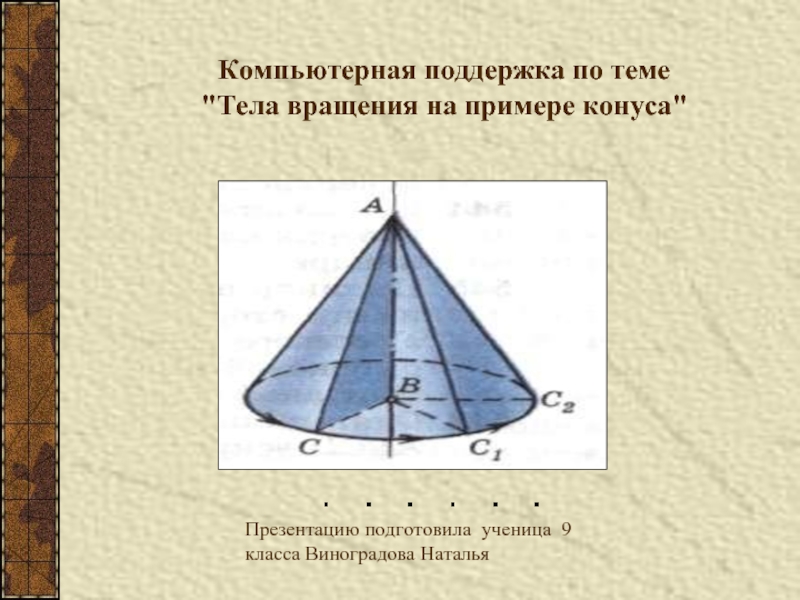
Слайд 1Презентацию подготовила ученица 9 класса Виноградова Наталья
Компьютерная поддержка по теме
"Тела
вращения на примере конуса"
Слайд 2Конус в переводе с греческого «konos» означает «сосновая шишка».
С
конусом люди знакомы с глубокой древности.
Много сделала для геометрии
школа Платона (428–348 гг. до н. э.). Школе Платона, в частности, принадлежит: а) исследование свойств призмы, пирамиды, цилиндра и конуса;
б) изучение конических сечений.
Историческая справка о конусе
Слайд 3Большой трактат о конических сечениях был написан Аполлонием Пергским– учеником
Евклида, который создал великий труд из 15 книг под названием
«Начала». Эти книги издаются и по сей день, а в школах Англии по ним учатся до сих пор.Историческая справка о конусе
Слайд 4Понятие конуса
Определение: тело, ограниченное конической поверхностью и кругом с
границей L, называется конусом.
Слайд 5боковая (коническая) поверхность
высота конуса (РО)
ось конуса
вершина конуса (Р)
основание конуса
радиус конуса
(r)
Элементы конуса
B
r
образующие
P
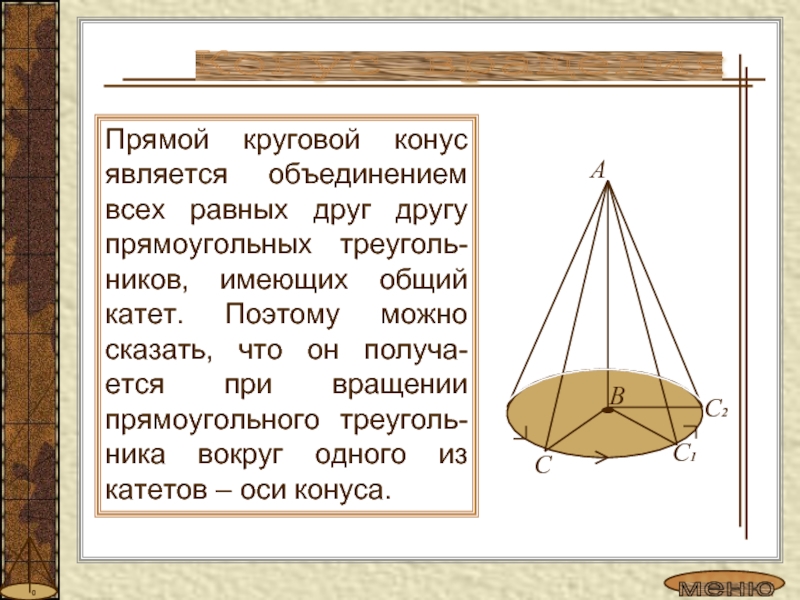
Слайд 6Прямой круговой конус является объединением всех равных друг другу прямоугольных
треуголь-ников, имеющих общий катет. Поэтому можно сказать, что он получа-ется
при вращении прямоугольного треуголь-ника вокруг одного из катетов – оси конуса.Конус вращения
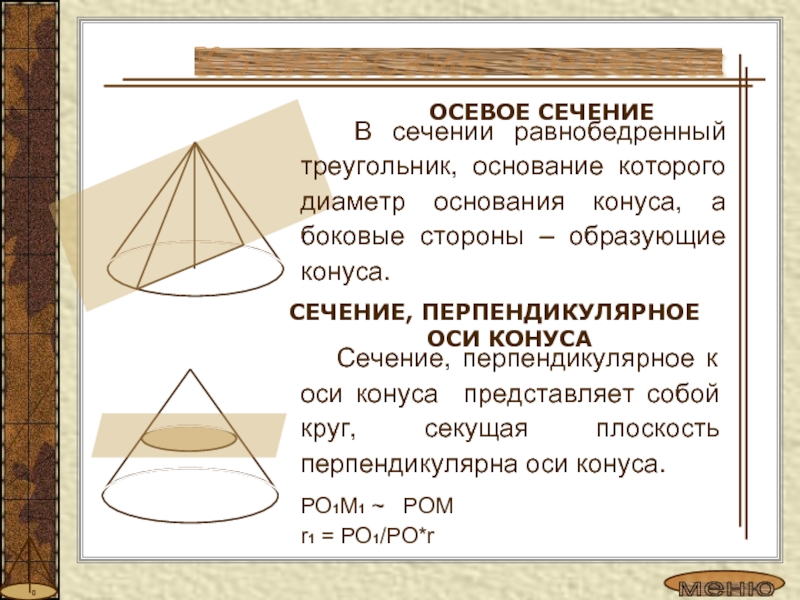
Слайд 7 Сечение, перпендикулярное к оси конуса представляет собой круг,
секущая плоскость перпендикулярна оси конуса.
РО1М1 ~ РОМ
r1 = РО1/РО*r
ОСЕВОЕ
СЕЧЕНИЕКонические сечения
СЕЧЕНИЕ, ПЕРПЕНДИКУЛЯРНОЕ ОСИ КОНУСА
В сечении равнобедренный треугольник, основание которого диаметр основания конуса, а боковые стороны – образующие конуса.
Слайд 11 За площадь боковой поверхности конуса принимается площадь его
развертки (конической поверхности).
1) Sбок =
Площадь боковой поверхности конуса
Слайд 12Площадь полной поверхности конуса
Площадь боковой поверхности конуса
равна произведению половины длины окружности основания на образующую. Площадью полной
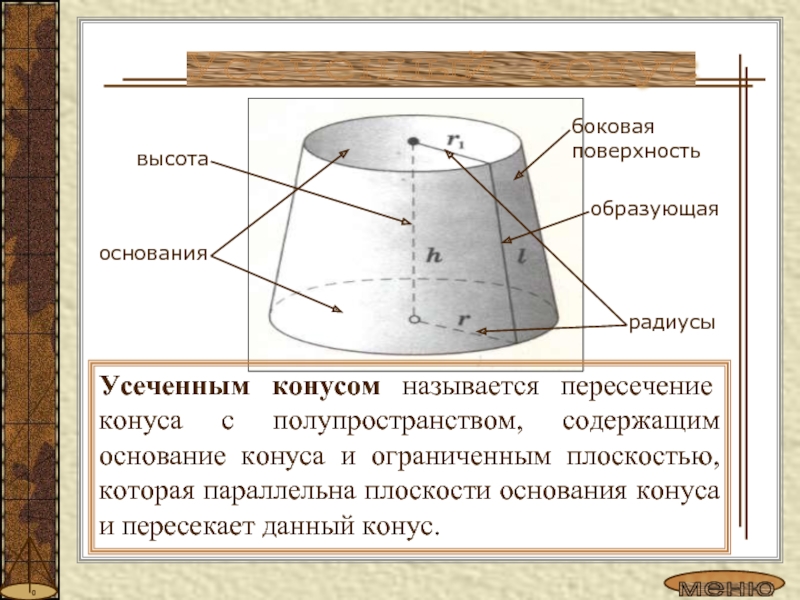
поверхности конуса называется сумма площадей боковой поверхности и основания.
Слайд 13Усеченным конусом называется пересечение конуса с полупространством, содержащим основание конуса
и ограниченным плоскостью, которая параллельна плоскости основания конуса и пересекает
данный конус.основания
образующая
радиусы
боковая поверхность
высота
Усеченный конус
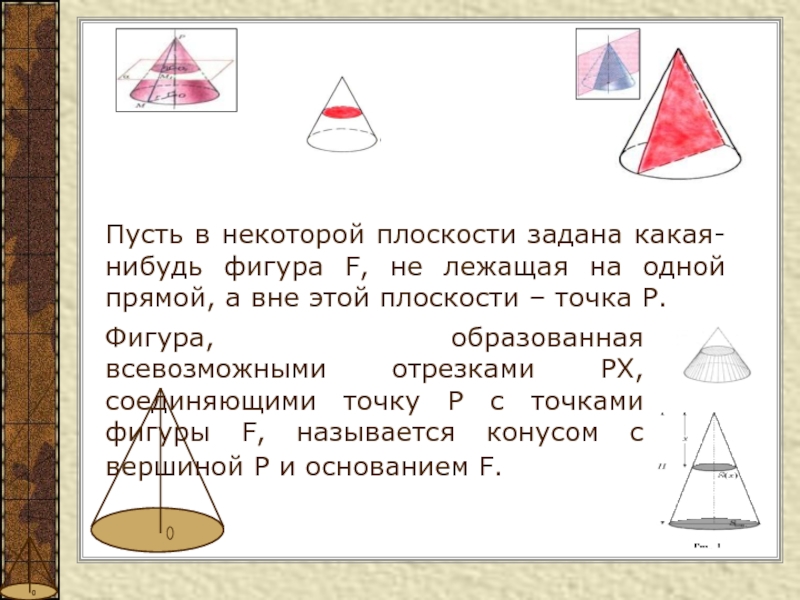
Слайд 14Пусть в некоторой плоскости задана какая-нибудь фигура F, не лежащая
на одной прямой, а вне этой плоскости – точка P.
Фигура, образованная всевозможными отрезками PX, соединяющими точку P с точками фигуры F, называется конусом с вершиной Р и основанием F.
Слайд 15Используемые ресурсы
http://ru.wikipedia.org/wiki/%D0%9A%D0%BE%D0%BD%D1%83%D1%81
http://images.yandex.ru/yandsearch?p=0&text=%D0%BA%D0%BE%D0%BD%D1%83%D1%81&img_url=900igr.net%2Fdatai%2Fgeometrija%2FObjom-konusa%2F0001-001-Obem-konusa.jpg&rpt=simage&noreask=1&lr=2
Теги
