Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Творческий проект "Современный урок математики, ориентированный на повышение качества знаний учащихся"
Содержание
- 1. Творческий проект "Современный урок математики, ориентированный на повышение качества знаний учащихся"
- 2. Цели: Познакомить с основными понятиями, тремя самыми
- 3. Аксиомы стереометрииУрок изучения и первичного закрепления новых
- 4. ПЛАНИМЕТРИЯСТЕРЕОМЕТРИЯ7-9 классы10-11 классыГЕОМЕТРИЯ на плоскостиГЕОМЕТРИЯ в пространстве«планиметрия» –
- 5. Основные понятия стереометрии точка,прямая,плоскость,расстояниеα = (РКС)|PK|A∉α ,
- 6. Аксиомы стереометрииСлово «аксиома» греческого происхождения и в
- 7. Аксиомы стереометрииА-1Через любые три точки, не лежащие
- 8. Аксиомы стереометрииА-2Если две точки прямой лежат в
- 9. Аксиомы стереометрииА-3Если две плоскости имеют общую точку,
- 10. СЛЕДСТВИЯ ИЗ АКСИОМТ-1Через любую прямую и не
- 11. СЛЕДСТВИЕ ИЗ Т-1Через две ПАРАЛЛЕЛЬНЫЕ прямые можно провести плоскость, и притом только одну. к
- 12. СЛЕДСТВИЯ ИЗ АКСИОМТ-2Через любые две пересекающиеся прямые
- 13. Опорный конспект Слайд № 14Слайд № 15
- 14. Аксиомы стереометрииСформулируйте содержание аксиом А1, А2, А3,
- 15. Следствия из аксиом стереометрииЧерез прямую и не
- 16. По трем точкам, не лежащим на одной
- 17. Сколько существует способов задания плоскости?Сколько плоскостей можно провести через выделенные элементы?ОТВЕТЬТЕ НА ВОПРОСЫ а)б)в)г)д)е)
- 18. Как при помощи двух нитей столяр может
- 19. Задача Дан тетраэдр МАBC, каждое ребро которого
- 20. Задача пересечение двух плоскостей ABCDA1B1C1D1 – куб,
- 21. Задача ABCD – ромб, О – точка
- 22. Тест Тест на компьютере
- 23. Любые три точки лежат в одной плоскости.Любые
- 24. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1
Творческий проект учителей математического цикла на тему:
«Современный урок математики,
ориентированный
на повышение качества знаний учащихся»
Слайд 2Цели:
Познакомить с основными понятиями, тремя самыми главными аксиомами и
следствиями из них.
Обеспечить высокое качество знаний учащихся по теме.
Задачи:
Создать условия
для усвоения основных понятий, аксиом, теорем.Сформировать умение работать с текстом учебника, таблицами, находить примеры на предметах окружающего мира, умение мыслить пространственно.
Содействовать развитию навыка самостоятельной работы учащихся посредством вовлечения их в исследовательскую деятельность (анализировать, наблюдать , делать выводы.)
Активизировать интерес к изучаемому материалу , используя практико-ориентированные задачи.
Слайд 3Аксиомы стереометрии
Урок изучения и первичного закрепления новых знаний.
«Старайтесь, прежде чем
приступить к выполнению любого задания на уроке или дома, чётко
определить вид своей деятельности»Слайд 4ПЛАНИМЕТРИЯ
СТЕРЕОМЕТРИЯ
7-9
классы
10-11
классы
ГЕОМЕТРИЯ на плоскости
ГЕОМЕТРИЯ в пространстве
«планиметрия» – наименование смешанного происхождения: от греч.
metreo – измерять
и лат. planum – плоская поверхность (плоскость)
«стереометрия» – от
греч. stereos – пространственный (stereon – объем). Школьный курс
ГЕОМЕТРИИ
Слайд 5Основные понятия стереометрии
точка,
прямая,
плоскость,
расстояние
α = (РКС)
|PK|
A∉α , KC ⊂
α , P ∈ α , |PK| =
2 смСлайд 6Аксиомы стереометрии
Слово «аксиома» греческого происхождения и в переводе означает истинное,
исходное положение теории.
Система аксиом стереометрии дает описание свойств пространства
и основных его элементов Понятия «точка», «прямая», «плоскость», «расстояние» принимаются без определений: их описание и свойства содержатся в аксиомах
Слайд 7Аксиомы стереометрии
А-1
Через любые три точки, не лежащие на одной прямой
проходит плоскость, и притом только одна
α = (РКС)
Слайд 8Аксиомы стереометрии
А-2
Если две точки прямой лежат в плоскости, то все
точки прямой лежат в этой плоскости.
m
М, C ∈ α
m
⊂ αМ, C ∈ m,
Если
то
Слайд 9Аксиомы стереометрии
А-3
Если две плоскости имеют общую точку, то они имеют
общую прямую, на которой лежат все общие точки этих плоскостей.
М
∈ α, М ∈ β, М ∈ mm ∈ α, m ∈ β
α ∩ β = m
Слайд 10СЛЕДСТВИЯ ИЗ АКСИОМ
Т-1
Через любую прямую и не принадлежащую ей точку
можно провести плоскость, и притом только одну.
м
А
В
Дано: М∉m
Так как
М∉m, то точки А, В и M не принадлежат одной прямой.
По А-1 через точки А, В и M проходит только одна плоскость — плоскость (ABM), Обозначим её α. Прямая m имеет с ней две общие точки — точки A и B, следовательно, по аксиоме А-2 эта прямая лежит в плоскости α..
Таким образом, плоскость α проходит через прямую m и точку M и является искомой.
Докажем, что другой плоскости, проходящей через прямую m и точку M, не существует. Предположим, что есть другая плоскость — β, проходящая через прямую m и точку M. Тогда плоскости α и β проходят через точки А, В и M, не принадлежащие одной прямой, а значит, совпадают. Следовательно, плоскость α единственна.
Теорема доказана
Доказательство
Пусть точки A, B ∈ m.
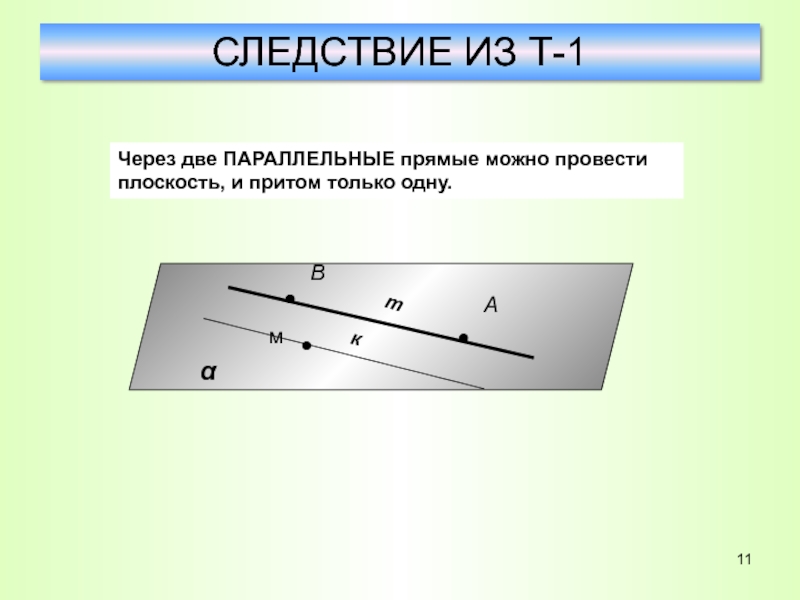
Слайд 11СЛЕДСТВИЕ ИЗ Т-1
Через две ПАРАЛЛЕЛЬНЫЕ прямые можно провести плоскость, и
притом только одну.
к
Слайд 12СЛЕДСТВИЯ ИЗ АКСИОМ
Т-2
Через любые две пересекающиеся прямые можно провести плоскость,
и притом только одну.
N
Дано: m ∩ n = M
Доказательство
Отметим
на прямой m произвольную точку N, отличную от М. Рассмотрим плоскость α =(n, N). Так как M∈ α и N∈α, то по А-2 m ⊂ α. Значит обе прямые m, n лежат в плоскости α и следовательно α, является искомой
Докажем единственность плоскости α. Допустим, что есть другая, отличная от плоскости α и проходящая через прямые m и n, плоскость β.
Так как плоскость β проходит через прямую n и не принадлежащую ей точку N, то по T-1 она совпадает с плоскостью α. Единственность плоскости α доказана.
Теорема доказана
Слайд 14Аксиомы стереометрии
Сформулируйте содержание аксиом А1, А2, А3, А4
Прокомментируйте их с
помощью приведенных ниже рисунков.
α
С
В
А
α
В
А
Через любые три точки, не лежащие на
одной прямой, проходит плоскость, и притом только одна.А, В, С ∉ одной прямой
А, В, С ∈ α
α - единственная плоскость
Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости.
А, В ∈ α, АВ ∈ α
Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.
С ∈ α, β;
α ∩ β = с;
С ∈ с.
Слайд 15Следствия из аксиом стереометрии
Через прямую и не лежащую на ней
точку проходит плоскость, и притом только одна.
Через две пересекающиеся прямые
проходит плоскость, и притом только одна.
Слайд 16По трем точкам, не лежащим на одной прямой
По прямой и
точке, не лежащей на этой прямой
По двум пересекающимся прямым
По двум
параллельным прямымКак в пространстве можно однозначно задать плоскость?
Слайд 17Сколько существует способов задания плоскости?
Сколько плоскостей можно провести через выделенные
элементы?
ОТВЕТЬТЕ НА ВОПРОСЫ
а)
б)
в)
г)
д)
е)
Слайд 18Как при помощи двух нитей столяр может проверить, лежат ли
концы четырёх ножек стола в одной плоскости?
?
Слайд 19
Задача
Дан тетраэдр МАBC, каждое ребро которого равно 6 см. D
принадлежит МВ, Е принадлежит МС, F принадлежит АВ, AF=FB, P
принадлежит МА. Дайте ответы на поставленные ниже вопросы с необходимыми обоснованиями.Назовите прямую, по которой пересекаются плоскости:
А) (МАВ) и (MFC) Б) (MCF) и (АВС)
2. Найдите длину отрезка CF и площадь треугольника АВС.
а) Объясните, как построить точку пересечения прямой DE с плоскостью (АВС)
б) Постройте точку пересечения прямой PD с плоскостью (АВС).
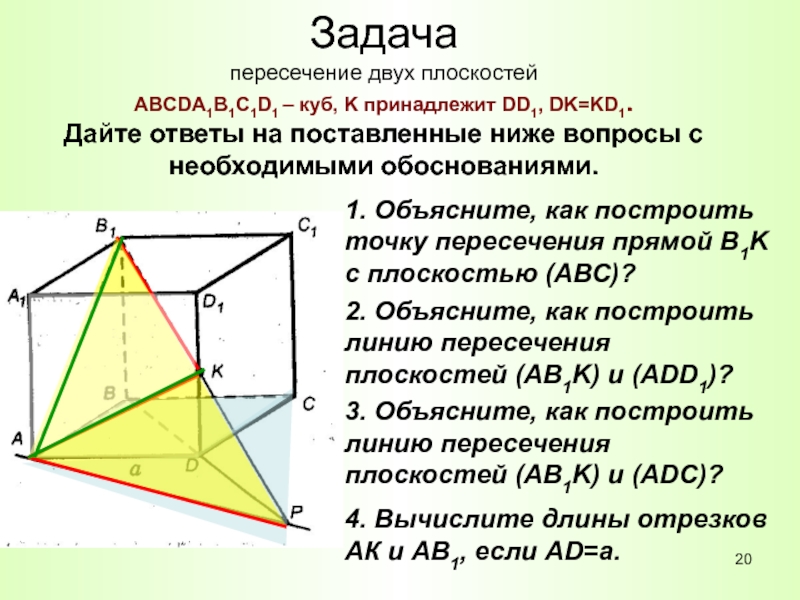
Слайд 20Задача пересечение двух плоскостей ABCDA1B1C1D1 – куб, K принадлежит DD1, DK=KD1. Дайте ответы
на поставленные ниже вопросы с необходимыми обоснованиями.
1. Объясните, как построить
точку пересечения прямой B1K с плоскостью (АВС)?2. Объясните, как построить линию пересечения плоскостей (AB1K) и (ADD1)?
3. Объясните, как построить линию пересечения плоскостей (AB1K) и (ADС)?
4. Вычислите длины отрезков АК и АВ1, если АD=a.
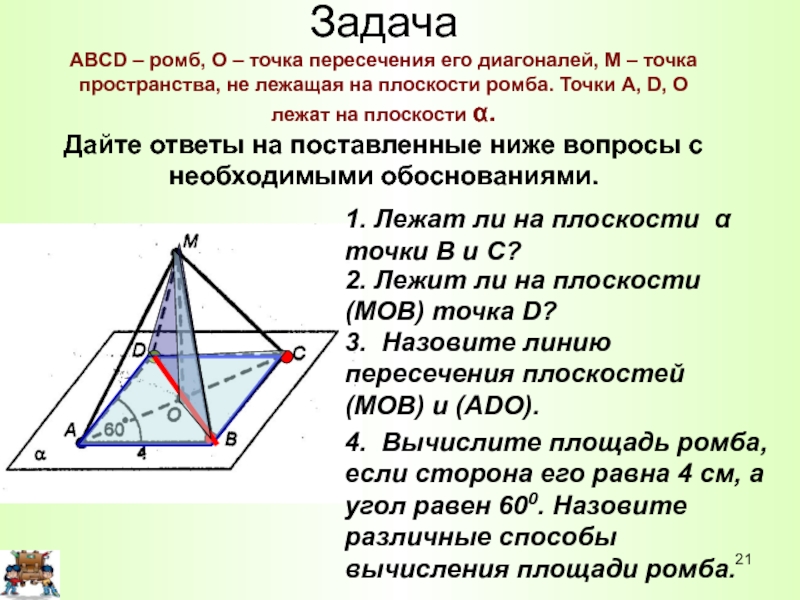
Слайд 21Задача ABCD – ромб, О – точка пересечения его диагоналей, М
– точка пространства, не лежащая на плоскости ромба. Точки A,
D, O лежат на плоскости α. Дайте ответы на поставленные ниже вопросы с необходимыми обоснованиями.1. Лежат ли на плоскости α точки В и С?
2. Лежит ли на плоскости (МОВ) точка D?
3. Назовите линию пересечения плоскостей (МОВ) и (ADO).
4. Вычислите площадь ромба, если сторона его равна 4 см, а угол равен 600. Назовите различные способы вычисления площади ромба.
Слайд 23Любые три точки лежат в одной плоскости.
Любые четыре точки лежат
в одной плоскости.
Любые четыре точки не лежат в одной плоскости.
Через
любые три точки проходит плоскость и при том только одна.Если прямая пересекает 2 стороны треугольника, то она лежит в плоскости треугольника.
Если прямая проходит через вершину треугольника, то она лежит в плоскости треугольника.
Если прямые не пересекаются, то они параллельны.
Если плоскости не пересекаются, то они параллельны.
В стереометрии мы будем рассматривать ситуации, задающие различные расположения в пространстве основных фигур относительно друг друга
Определите: верно, ли суждение?
ДА
ДА
ДА
НЕТ
НЕТ
НЕТ
НЕТ
НЕТ