Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Учимся решать задачи на смеси и сплавы
Содержание
- 1. Учимся решать задачи на смеси и сплавы
- 2. Немного теорииДля решения данного вида
- 3. Процентным содержанием
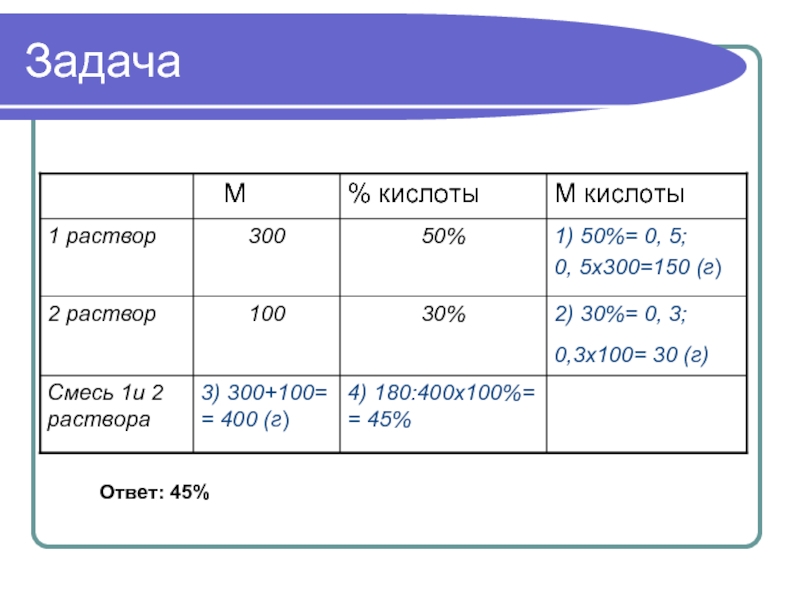
- 4. Задача
- 5. ЗадачаОтвет: 45%
- 6. Алгоритм решения задач такого
- 7. Слайд 7
- 8. Слайд 8
- 9. При решении задач данного типа
- 10. Пример 1. Имеются два
- 11. Сверху подпишем названия компонентов
- 12. В результате получим следующую модель
- 13. Слайд 13
- 14. Первый способ Пусть масса первого сплава х
- 15. Второй способ.Можно обозначить х г и у
- 16. Замечание.Обратите внимание на то,
- 17. Пример 2. В 4 кг сплава меди
- 18. Пример 3. Свежие грибы содержат 90% влаги,
- 19. Можно составить уравнение на
- 20. Пример 4. Из 40 т железной руды
- 21. Задача. Из бака емкостью 54 л, наполненного
- 22. Однако работа
- 23. 54х-х² =1620-54х;
- 24. Задача 6Слиток сплава серебра с цинком весом
- 25. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Работа ученицы 7 класса Г
МОУ «СОШ № 24»г. Северодвинска
Лысковской Татьяны
Учитель
математики Паршева В.В.
Слайд 2 Немного теории
Для решения данного вида задач необходимо знать,
что такое концентрация вещества в смеси (растворе или сплаве). Пусть
в смесь входят компоненты А, В и С с массами тА, тВ, тС соответственно. Будем считать, что масса т смеси равна сумме масс компонентов, т.е. т = = тА + тВ + тС. Тогда концентрацией компонента А по массе будем называть отношение массы этого компонента к массе всей смеси и обозначать как СА :Аналогично для компонентов В и С
Концентрация — безразмерная величина. Понятно, что сумма концентраций всех компонентов смеси равна 1 (СА + СВ + СС = 1).
Слайд 3
Процентным содержанием компонента А
называется число
рА= сА 100%, т.е. это
концентрация вещества, выраженная в процентах.Аналогично рВ= сВ 100% и
рС = сС 100%.
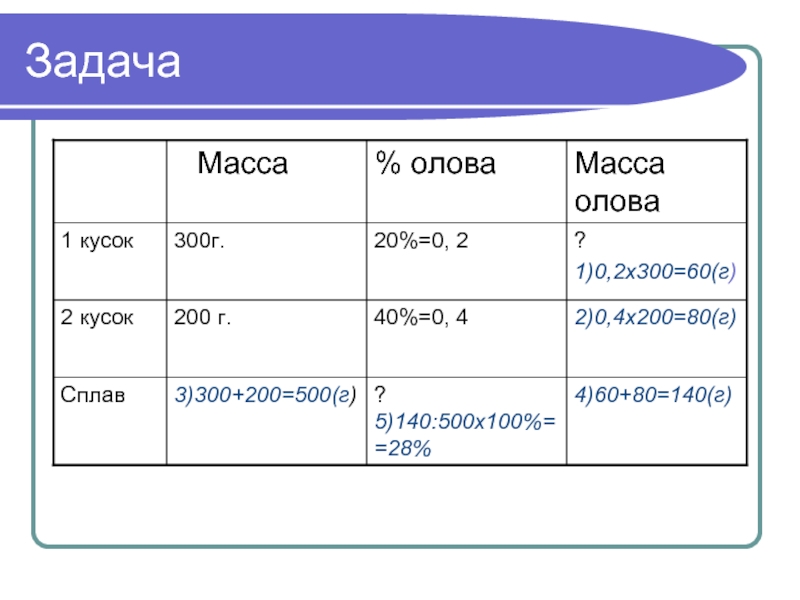
Слайд 6 Алгоритм решения задач такого типа
1)
2)
3)
4)
5)
Масса олова
в первом куске.
Масса олова во втором куске.
Масса олова в двух
кусках.Масса сплава в двух кусках.
Процентное содержание олова в двух кусках.
Слайд 9 При решении задач данного типа полезно пользоваться наглядной
моделью — схемой, в которой смесь (раствор, сплав) изображается в
виде прямоугольника, разбитого на фрагменты в соответствии с числом входящих в нее (в него) компонентов, а непосредственно при составлении уравнения — проследить содержание какого-нибудь одного компонента.Слайд 10 Пример 1. Имеются два сплава меди со
свинцом. Один сплав содержит15% меди, а другой 65%. Сколько нужно
взять каждого сплава, чтобы получилось 200 г сплава, содержащего 30% меди? Решение. Изобразим каждый сплав в виде прямоугольника,
разбитого на два фрагмента. Поскольку данные сплавы соединяют в новый (на схеме эту операцию обозначим знаком « + » между прямоугольниками, а тот факт, что третий сплав — результат смешения первых двух, покажем с помощью знака «=») и он содержит те же самые компоненты, изобразим получающийся сплав в виде такого же прямоугольника
Слайд 11 Сверху подпишем названия компонентов сплавов. Обычно бывает
достаточно указать первые буквы в их названиях (если они различны).
В данном случае — это буквы М (медь) и С (свинец).Теперь внутри соответствующих фрагментов каждого прямоугольника запишем данное в условии процентное содержание элементов (в нашем примере только меди), а под прямоугольником укажем массу сплава (нам известна только масса третьего сплава).
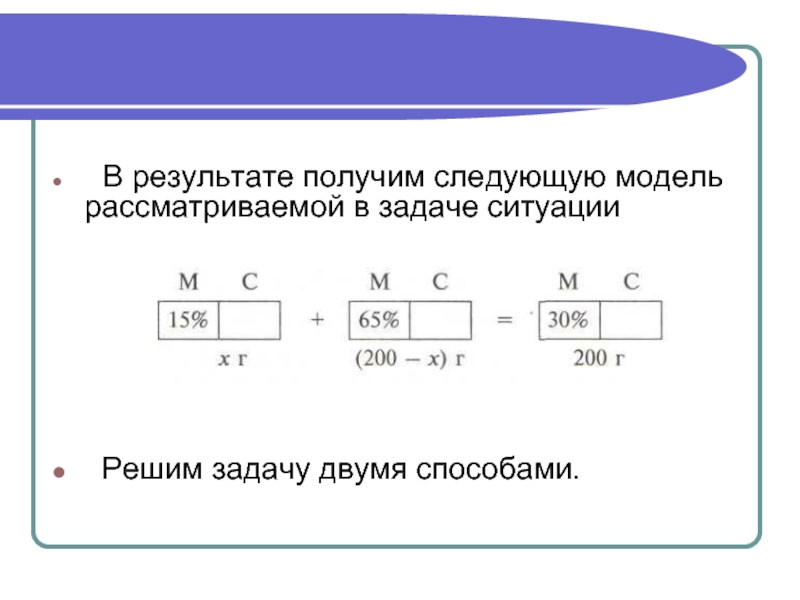
Слайд 12 В результате получим следующую модель рассматриваемой в задаче
ситуации
Решим задачу двумя способами.
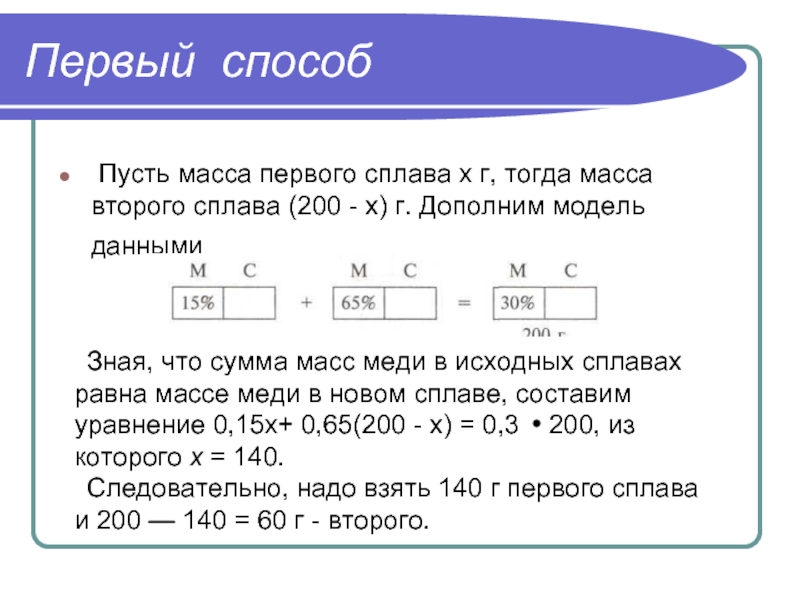
Слайд 14Первый способ
Пусть масса первого сплава х г, тогда масса
второго сплава (200 - х) г. Дополним модель данными
Зная,
что сумма масс меди в исходных сплавах равна массе меди в новом сплаве, составим уравнение 0,15х+ 0,65(200 - х) = 0,3 200, из которого х = 140.Следовательно, надо взять 140 г первого сплава и 200 — 140 = 60 г - второго.
Слайд 15Второй способ.
Можно обозначить х г и у г массу первого
и второго сплава соответственно.
Очевидно, х + у = 200 —
первое уравнение системы. Второе уравнение получим, приравняв сумму масс
меди в исходных сплавах и в новом сплаве. Таким образом,
Слайд 16 Замечание.
Обратите внимание на то, что в любом
из рассмотренных способов решения можно было составить уравнение и на
основе подсчета масс свинца. Ясно, что если в первом сплаве медь составляет 15% от его общей массы, то на свинец приходится 85%. Аналогично во втором и третьем сплавах свинца будет 35% и 70% соответственно. Тогда, решая задачу первым способом, получим уравнение0,85х + 0,35(200 - х) = 0,7 200.
Очевидно, оно равносильно уравнению 0,15х + 0,65(200 - х) = 0,3 200.
Из двух возможных уравнений обычно выбирают то, что проще составить по условию задачи или легче будет решить.
Слайд 17Пример 2. В 4 кг сплава меди и олова содержится
40% олова. Сколько килограммов олова надо добавить к этому сплаву,
чтобы содержание олова в новом сплаве было равно 70%?
Решение. Обозначим компоненты сплава буквами М (медь) и О (олово). Пусть к сплаву надо добавить х кг олова, тогда масса нового сплава будет равна (4 + х) кг. Составим модель рассматриваемой в задаче ситуации.
Так как сумма масс олова, указанных в левой части схемы (до смешения сплавов), равна массе олова в новом сплаве, можно составить уравнение
0,4 • 4 + х = 0,7(4 + х), откуда х = 4.
Ответ: 4 кг.
Слайд 18Пример 3. Свежие грибы содержат 90% влаги, а сушеные —
12% влаги. Сколько сушеных грибов получится из 10 кг свежих?
Решение.
Введем обозначения: ГМ — грибная масса, В — вода (влага). Процесс сушки грибов состоит в удалении из них большей части влаги. Если принять за х кг массу сушеных грибов, то масса удаленной влаги будет равна (10 - х) кг. Теперь нетрудно составить необходимую для дальнейшего решения схемуСлайд 19 Можно составить уравнение на основе подсчета масс
влаги, учитывая, что она удаляется из грибов:
0,9
10-(10-х) = 0,12х.Однако поступим иначе. Найдем процентное содержание грибной массы в свежих и в сушеных грибах и, учитывая, что она в результате сушки не изменилась, составим уравнение 0,1 • 10 = 0,88х.
Ясно, что второе уравнение проще первого. Решив его, найдем
Ответ: .
Слайд 20Пример 4. Из 40 т железной руды выплавляют 20 т
стали, содержащей 6% примесей. Каков процент примесей в руде?
Решение. Воспользуемся
следующими обозначениями: Ж — железо в руде и стали, П — примеси. В процессе плавки удаляется большая часть примесей. Пусть в руде их содержится х %. Составим вспомогательную схему:Рассуждая, как и в предыдущей задаче, придем к уравнению
0,01 • х • 40 - 20 = 0,06 • 20.
Или, выразив процентное содержание железа в руде и стали:(100 -х)% и 94% соответственно, приравняем массы железа в обоих случаях, получим равносильное уравнение0,01 • (100 - х) • 40 = 0,94 • 20, откуда х = 53.
Ответ: 53%.
Слайд 21Задача. Из бака емкостью 54 л, наполненного кислотой, вылили несколько
литров и долили водой. Потом опять вылили столько же литров
смеси, после чего в баке осталось 24 л чистой кислоты. Сколько кислоты вылили в первый раз?Решение. Введем обозначения: К — кислота, В — вода. Пусть х л - количество кислоты, отлитой из бака в первый раз. Описанную в задаче ситуацию можно представить в виде следующей схемы
Пример 5
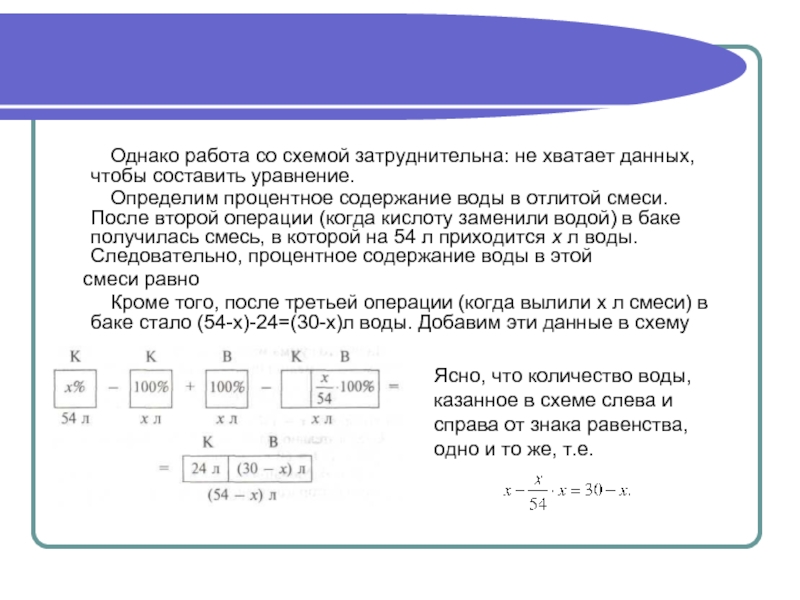
Слайд 22 Однако работа со схемой затруднительна:
не хватает данных, чтобы составить уравнение.
Определим процентное содержание воды в отлитой смеси. После второй операции (когда кислоту заменили водой) в баке получилась смесь, в которой на 54 л приходится х л воды. Следовательно, процентное содержание воды в этойсмеси равно
Кроме того, после третьей операции (когда вылили х л смеси) в баке стало (54-х)-24=(30-х)л воды. Добавим эти данные в схему
Ясно, что количество воды,
казанное в схеме слева и
справа от знака равенства,
одно и то же, т.е.
Слайд 23 54х-х² =1620-54х;
х² -108х+1620=0.
Корни уравнения: х=90, х=18. Первый корень не подходит
по смыслу задачи (нельзя отлить 90л из бочки, вмещающей всего 54л).Ответ:18л
Слайд 24Задача 6
Слиток сплава серебра с цинком весом в 3.5 кг
содержал 76% серебра. Его сплавили с другим слитком и получили
слиток весом в 10.5 кг, содержание серебра в котором было 84%. Сколько процентов серебра содержалось во втором слитке?Решение:
1) 3.5-0.76 = 2.66 (кг) серебра в первом слитке.
2) 10.5-0.84 = 8.82 (кг) серебра в 10.5 кг сплава.
3) 8.82 - 2.66 = 6.16 (кг) серебра во втором слитке.
4) 10.5 - 3.5 = 7 (кг) вес второго слитка.
5) 6.16: 7 = 0.88 = 88% серебра содержалось во втором слитке.
Ответ: 88% серебра содержалось во втором слитке.