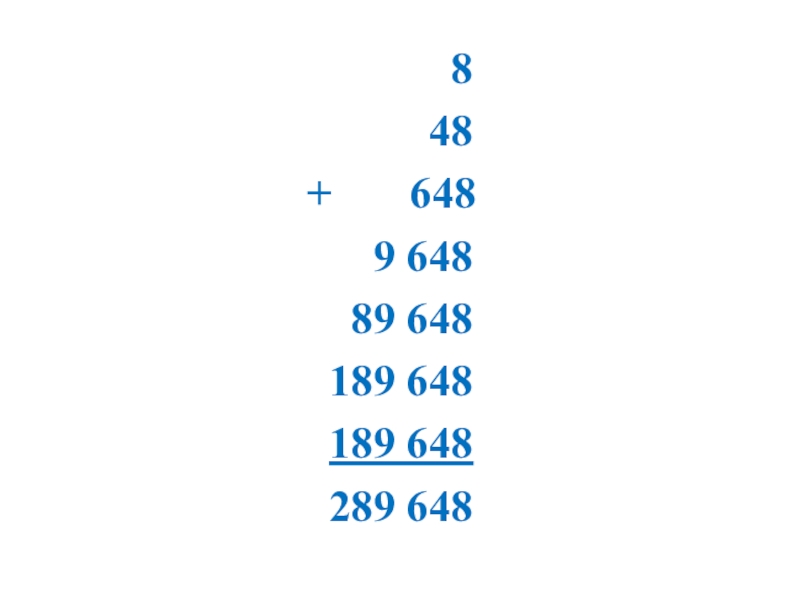Внеурочная деятельность по математике

№5» г.Ухты
Республики Коми
Стебакова И.Г.
2015 год

сделать его немного занимательным"

математике как части общечеловеческой культуры, о значимости математики в развитии

цивилизации и современного общества;

конференции.
Математические вечера.
Устный журнал.

сечением и даже “божественной пропорцией”.
Вы узнаете какую роль играет

эта пропорция в окружающем мире, как она связана с понятием гармонии и как и почему она используется в искусстве (живописи, архитектуре, фотографии…), дизайне…

дизайне золотое сечение очень часто используется в виде классических приемов

композиции, о чем вы можете прочитать, заглянув на любой сайт, посвященный этим видам искусства.]
Основная рекомендация заключается в следующем. Объект, являющийся центральной фигурой в композиции, далеко не всегда должен располагаться в центре. Определенные точки в композиции автоматически привлекают внимание. Таких точек 4, и расположены они на расстоянии 3/8 и 5/8 от краев картины. Нарисовав сетку, получим эти точки в местах пересечения линий (см. фотографию).

отрезка на неравные части. При котором длина всего отрезка так

относится к его большей части, как длина большей части относится к длине меньшей.









Это отношение равно иррациональному числу Ф=1.618033989..
Впервые золотое сечение встречается в «Началах» Евклида (300 лет до н.э.). Лука Пачоли, современник Леонарда да Винчи, назвал его «божественной пропорцией».
Золотое сечение обозначают символами PHI или Ф (в честь древнегреческого скульптора Фидия, всегда использовавшего в своих работах золотое сечение).
Математик Фибоначчи впервые получил последовательность чисел, названной в его честь числами Фибоначчи 1,1,2,3,5,8,13,21,34,55 …
Особенностью этого числового ряда является то, что каждый его член, начиная с третьего, равен сумме двух предыдущих : 1+1=2; 1+2=3; 2+3=5; 3+5=8 …При этом отношение двух соседних членов равно золотому сечению, т.е. числу Ф.
Рассматривая закономерности, связанные с проявлением золотого сечения, обычно используют обратную величину числа Ф : 1/1,618 = 0,618

a+b

a b

b : a = (a+b) : b

пирамиды Хеопса, знаменитый греческий храм Парфенон, большинство греческих скульптур памятников,

непревзойденная Джоконда Леонарда да Винчи, картины Рафаэля, Шишкина, этюды Шопена, музыка Бетховена, Чайковского, стихи Пушкина … вот далеко не полный перечень выдающихся произведений искусства, наполненных чудесной гармонией основанной на золотом сечении.

На фотографии показаны здания, при делении основных масс конструкций которых использовалось золотое сечение.
Обычно считается, что такое членение используется в зданиях, построенных в классическом стиле. Однако, посмотрите на Смольный собор, построенный в стиле барокко, и вы без труда обнаружите золотое сечение.

3 угла, если один срезать, сколько останется?
Чему равна одна четвёртая

часть часа?
Сколько концов у 3,5 палок?
Шла старуха в Москву, а на встречу ей три старика. Сколько человек шло в Москву?
Петух весит на одной ноге 4кг. Сколько весит петух на двух ногах?
Бежала тройка лошадей. Каждая пробежала 5км. Сколько км проехал ямщик?
Три курицы за три дня снесут три яйца. Сколько яиц снесут двенадцать кур за двенадцать дней?
На елке горело 7 свечей, 5 из них погасли. Сколько свечей осталось?
Две дочери, две матери, да бабушка с внучкой. Сколько всех?
Сколько надо сделать распилов, чтобы распилить бревно на 12 частей?
7 человек обменялись фотографиями, сколько было роздано фотографий?

восемь, не собьюсь,..."

65
+ 465
9 465
19 465
29 465

48

+ 648
9 648
89 648
189 648
189 648
289 648

7

17
417
3 417
53 417
+ 453 417
7 453 417
67 453 417
567 453 417
3 567 453 417
73 567 453 417
77 777 777 777