Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Возрастание и убывание функции
Содержание
- 1. Возрастание и убывание функции
- 2. Числовые промежутки[α;b] – отрезок(α;b) – интервал(α;b] – полуинтервал[α;b) - полуинтервал
- 3. Функция f(x) называется возрастающей на некотором промежутке,
- 4. Функция f(x) называется убывающей на некотором промежутке,
- 5. Теорема Лагранжа Пусть функция f(х) непрерывна
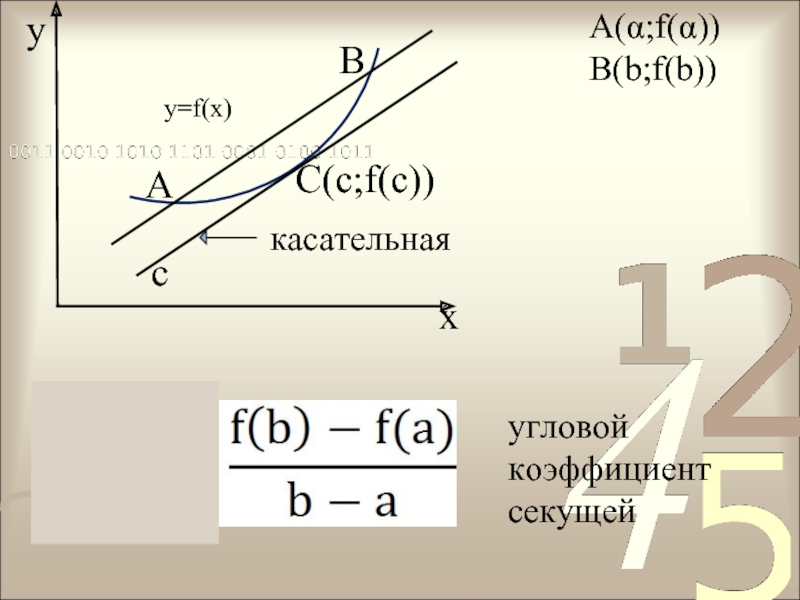
- 6. yxABкасательнаясA(α;f(α))B(b;f(b))y=f(x)угловой коэффициент секущейC(c;f(с))
- 7. Достаточные условия возрастания и убывания функции
- 8. доказательство: Пусть х1 и х2 - произвольные
- 9. Скачать презентанцию
Числовые промежутки[α;b] – отрезок(α;b) – интервал(α;b] – полуинтервал[α;b) - полуинтервал
Слайды и текст этой презентации
Слайд 1Возрастание и убывание функции.
Рано или поздно всякая правильная математическая идея
находит применение в том или ином деле.
![Числовые промежутки[α;b] – отрезок(α;b) – интервал(α;b] – полуинтервал[α;b) - полуинтервал](/img/thumbs/71b9275e4387a4912c487f44709d810f-800x.jpg "Возрастание и убывание функции Числовые промежутки[α;b] – отрезок(α;b) – интервал(α;b] – полуинтервал[α;b) - полуинтервал")
Слайд 3Функция f(x) называется возрастающей на некотором промежутке, если большему значению
аргумента соответствует большее значение функции.
x1 > x2 ⬄ f(x1
) > f(x2)
Слайд 4Функция f(x) называется убывающей на некотором промежутке, если большему значению
аргумента соответствует меньшее значение функции.
x1 > x2 ⬄ f(x1
) < f(x2)
Слайд 5Теорема Лагранжа
Пусть функция f(х) непрерывна на отрезке [α;b]
и дифференцируема на интервале (α;b). Тогда существует точка с €
(α;b), такая, чтоf(b) – f(α) = f ′(c) (b - α)
![Теорема Лагранжа Пусть функция f(х) непрерывна на отрезке [α;b] и дифференцируема на интервале (α;b). Тогда существует](/img/thumbs/47d1285251203002ad3f39dbb9e93a95-800x.jpg "Возрастание и убывание функции Теорема Лагранжа Пусть функция f(х) непрерывна на отрезке [α;b] и дифференцируема")
Слайд 7Достаточные условия возрастания и убывания функции
Пусть функция f(х)
непрерывна на отрезке [α;b] и дифференцируема на интервале (α;b). Тогда
если f′(x)>0 для всех х € (α;b) ,то функция f(x) возрастает на отрезке [α;b] ,
а если f′(x)<0 для всех х € (α;b) ,
то функция f(x) убывает на отрезке [α;b] .
![Достаточные условия возрастания и убывания функции Пусть функция f(х) непрерывна на отрезке [α;b] и дифференцируема на](/img/thumbs/0167454779f0ae5aead68f1c6f075594-800x.jpg "Возрастание и убывание функции Достаточные условия возрастания и убывания функции Пусть функция f(х) непрерывна на")
Слайд 8доказательство:
Пусть х1 и х2 - произвольные точки отрезка [α;b]
, такие, что х1 < х2 , т.е. х2- х1
>0По теореме Лагранжа
При f′(x)>0 f(х2) – f(х1) > 0 ⬄ функция возрастает.
При f′(x)<0 f(х2) – f(х1) < 0 ⬄ функция убывает.
f(х2) – f(х1) = f ′(х) (х2- х1), х € (α;b)
![доказательство: Пусть х1 и х2 - произвольные точки отрезка [α;b] , такие, что х1 < х2 ,](/img/thumbs/e76145811eb65467523865c288eba050-800x.jpg "Возрастание и убывание функции доказательство: Пусть х1 и х2 - произвольные точки отрезка [α;b] ,")
Теги
