Вписанная и описанная окружность

основаниям
Если О- центр вписанной окружности, то СОD =90

3.Если

СM=CH
MD=KD

равен радиусу окружности, описанной около треугольника, вершинами которого являются любые

О – центр описанной окружности около ABD и трапеции ABCD

описанной около трапеции окружности.
Решение:
Радиус R описанной окружности около трапеции –

D=2R=

Ответ.21,25

и синус угла (острого) при основании равен 0.8. Найти площадь

О – центр вписанной окружности – середина серединного перпендикуляра к основаниям трапеции. ВК – высота трапеции.
S =MN BK
Т.к. окружность вписана в трапецию, то BC+AD=AB+CD
Т.к. AB+CD, то BC+AD=2AB
MN=

Значит 2MN=2AB=5

ABK: BK=ABsinA= 5

0.8=4

S=5 4=20

Ответ. 20

трапеции равна 27, а основания 48 и 30. найти радиус

А

КH – высота, КН – срединный перпендикуляр
ОА=ОВ=R
Пусть OH=х, тогда ОК=КН-ОН=27-х
AOH: AO

Тогда

54х=378
Х=7

R=OA=

Ответ.25

стороной делит эту сторону на отрезки 1 см и 4см.

СD=CH+HD=1+4=5

O - центр вписанной окружности в трапецию, значит

COD=90

Тогда

R=OH=2

Значит АВ=2r=2

2

=4

CKD: KD=

MC= CH=1, т.к. O- центр вписанной окружности
BC=BM+CM=2+1=3, AD=AK+KD=3+3=6, P=4+3+5+6=18

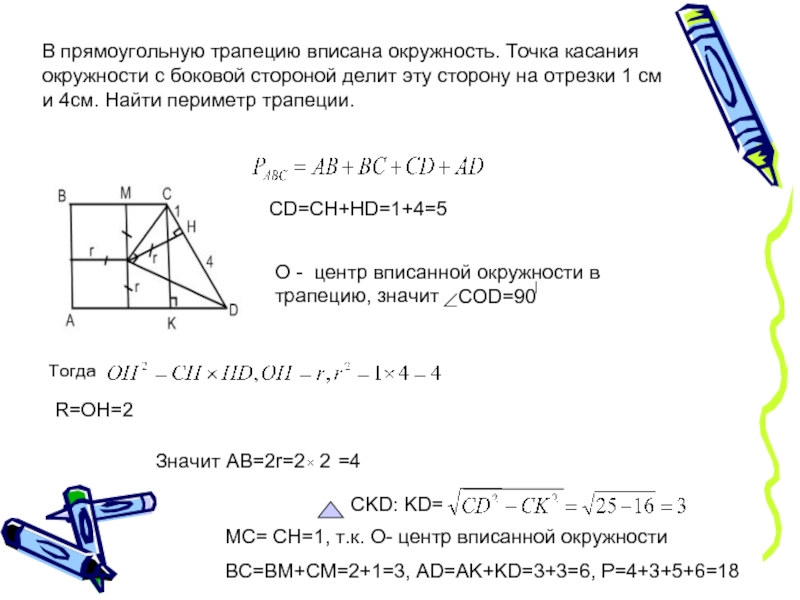
а её площадь равна
Найти радиус окружности, вписанной в эту

Ответ.3.

2.Окружность описана около равнобедренной трапеции ABCD с основанием AD=15 AC и BD образуют с боковой стороной AB углы ВАС= , ABD= также, что sin

MN средняя линия трапеции. Найти MN.

Ответ.12.

3.Около трапеции описана окружность, центр которой лежит на основании AD.

Средняя линия равна 6.

Найти радиус описанной окружности.

Ответ.4.

4.Равнобедренная трапеция описана около окружности радиуса 2.
Найти площадь трапеции, если косинус угла при большем основании трапеции равен 0,6

Ответ.20.

5.Средняя линия прямоугольной трапеции равна 9,а радиус вписанной окружности в неё равен 4. Найти большее основание трапеции.

Ответ.12