Вписанные углы

Содержание

1. Вписанные углы
2. Устная работаДано: ∪АВ : ∪ВС : ∪АС=2:3:4
3. Угол вершина которого лежит на окружности, а
4. Вписанный угол измеряется половиной дуги на которую
5. Рассмотрим 1 случай расположения луча ВО относительно
6. Рассмотрим 2 случай, когда луч ВО делит
7. Рассмотрим 3 случай расположения луча ВО относительно
8. РАССМОТРИМ 1 СЛЕДСТВИЕ ИЗ ТЕОРЕМЫВписанные углы , опирающиеся на одну и ту же дугу, равны.
9. Рассмотрим 2 следствие из теоремыВписанный угол, опирающийся на полуокружность − прямой.
10. Скачать презентанцию

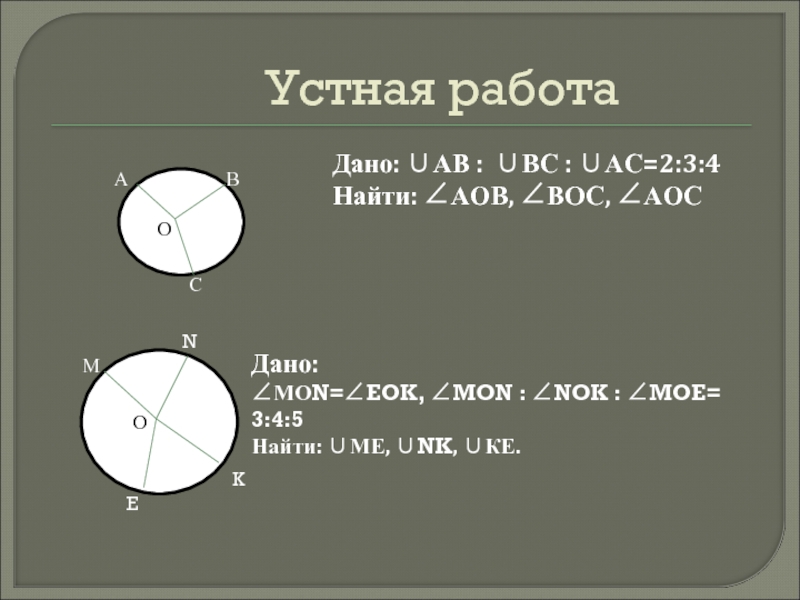
Устная работаДано: ∪АВ : ∪ВС : ∪АС=2:3:4 Найти: ∠АОВ, ∠ВОС, ∠АОСДано: ∠МОN=∠EOK, ∠MON : ∠NOK : ∠MOE= 3:4:5Найти: ∪МЕ, ∪NK, ∪КЕ.

Слайды и текст этой презентации

Слайд 1Урок геометрии в 8 классе «Вписанные углы»
Учитель математики БОУСОШ №1 Колокольцева

А.В.

Слайд 2Устная работа
Дано: ∪АВ : ∪ВС : ∪АС=2:3:4
Найти: ∠АОВ, ∠ВОС,

∠АОС
Дано:
∠МОN=∠EOK, ∠MON : ∠NOK : ∠MOE= 3:4:5
Найти: ∪МЕ, ∪NK,

∪КЕ.

Устная работаДано: ∪АВ : ∪ВС : ∪АС=2:3:4 Найти: ∠АОВ, ∠ВОС, ∠АОСДано: ∠МОN=∠EOK, ∠MON : ∠NOK : ∠MOE=

Слайд 3Угол вершина которого лежит на окружности, а стороны пересекают окружность,

называется вписанным углом. Вписанный ∠ АВС опирается на ∪ АМС.

Вписанный угол

Угол вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным углом. Вписанный ∠ АВС опирается

Слайд 4Вписанный угол измеряется половиной дуги на которую он опирается
Пусть ∠

АВС – вписанный угол окружности с центром О, опирающийся на

∪ АС. Докажем, что ∠ АВС = половине ∪ АС (на которую он опирается). Существует 3 возможных случая расположения луча ВО относительно ∠ АВС. Рассмотрим их.

Вписанный угол измеряется половиной дуги на которую он опираетсяПусть ∠ АВС – вписанный угол окружности с центром

Слайд 5Рассмотрим 1 случай расположения луча ВО относительно ∠ АВС.
Например луч

совпадает со стороной ВС в этом случае ∪ АС меньше

полуокружности, поэтому ∠ АОС= ∪ АС. Так как ∠ АОС − внешний угол равнобедренного Δ АВО, а ∠ 1 и ∠ 2 при основании равнобедренного треугольника равны, то ∠ АОС = ∠ 1+ ∠ 2 = 2∠1. Отсюда следует, что 2∠1 = ∪АС или ∠ АВС = ∠ 1 = 1/2 ∪ АС.

Рассмотрим 1 случай расположения луча ВО относительно ∠ АВС.Например луч совпадает со стороной ВС в этом случае

Слайд 6Рассмотрим 2 случай, когда луч ВО делит ∠ АВС на

два угла.
В этом случае луч ВО пересекает ∪ АС в

некоторой точке D. Точка D разделяет ∪ АС на две дуги: АD и DC. По доказанному в п.1 ∠ АВD = 1/2 ∪AD и ∠ DBC= 1/2 ∪ DC. Складывая эти равенства попарно, получаем: ∠ ABD + ∠ DBC = 1/2 ∪ АD + 1/2 ∪ DC, или ∠ АВС= 1/2 ∪ АС.

Рассмотрим 2 случай, когда луч ВО делит ∠ АВС на два угла.В этом случае луч ВО пересекает

Слайд 7Рассмотрим 3 случай расположения луча ВО относительно ∠ АВС
 АВD−

равнобедренный, ∠ AOD - внешний, т.к.  ABD - равнобедр.

То ∠ 1 = ∠ 2 => ∠ AOD = ∠ 1 + ∠ 2 = 2∠1 = ∪ AD, следовательно ∠ ABD = 1/2 ∪ AD.
Аналогично:  ВСО равнобедр. ∠ COD - внешний, следовательно ∠ СВD= 1/2 ∪ CD.
Следовательно, ∠ АВС=1/2 ∪ АС