Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Задачи на клетчатой бумаге
Содержание
- 1. Задачи на клетчатой бумаге
- 2. Содержание.Глава 1. Введение. Цель и задачи
- 3. Слайд 3
- 4. Глава.1 Введение. Цель и
- 5. Гипотеза: многообразие задач на бумаге в
- 6. Глава 2. Формула Пика Линии, идущие по
- 7. Пусть АВСD – прямоугольник с вершинами
- 8. Это и есть формула Пика.
- 9. . Проверить формулу Пика для многоугольника на
- 10. Если многоугольник можно разрезать на треугольники с
- 11. Глава 3. Задачи на клетчатой бумаге в контрольно-измерительных материалах ЕГЭ по математике.
- 12. На клетчатой бумаге с клетками размером 1
- 13. Найдите площадь четырехугольника, изображённого на рисунке
- 14. Глава 4. Заключение.В процессе исследования рассмотрены задачи
- 15. Глава 5. БиблиографияЖарковская Н. М., Рисс Е.
- 16. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1 Задачи
на клетчатой бумаге. Формула Пика.
Автор: Корнева Валентина
Николаевна
учитель математики МОУ Романовская СОШСлайд 2Содержание.
Глава 1. Введение. Цель и задачи работы.
Глава 2.
Формула Пика.
Глава 3. Задачи на клетчатой бумаге
в материалах ЕГЭ Глава 4. Заключение.
Глава 5. Библиография.
Слайд 3
«Решение задач – практическое искусство, подобное плаванию, катанию на лыжах или игре на фортепиано; научиться ему можно, только подражая хорошим образцам и постоянно практикуясь» Д. Пойя
Слайд 4 Глава.1 Введение. Цель и задачи работы.
При решении
задач обучающиеся часто оказываются в затруднении при встрече с задачами
на клетчатой бумаге. Возникли вопросы: в чём заключается особенность таких задач, существуют ли специальные методы и приёмы решения задач на клетчатой бумаге.Слайд 5 Гипотеза: многообразие задач на бумаге в клеточку, их «занимательность»,
отсутствие общих правил и методов решения вызывают у школьников затруднения
при их рассмотренииПри более внимательном исследовании задач на клетчатой бумаге, мы убедимся в их востребованности, оригинальности, полезности.
Слайд 6Глава 2. Формула Пика
Линии, идущие по сторонам клеток, образуют
сетку, а вершины клеток – узлы этой сетки. Нарисуем на
листе многоугольник с вершинами в узлах (рис. 1) и найдем его площадь. Искать её можно по-разному. Например, можно разрезать многоугольник на достаточно простые фигуры, найти их площадь и сложить.Но тут нас ждёт много хлопот (попробуйте!). Давайте «схитрим»:
вычислим площадь заштрихованной фигуры, которая «дополняет» наш
многоугольник до прямоугольника АВСD, и вычтем её из площади прямоугольника. Заштрихованная фигура легко разбивается на прямоугольники и прямоугольные треугольники, и её площадь вычисляется без усилий.
Слайд 7
Пусть АВСD – прямоугольник с вершинами в узлах и
сторонами, идущими по линиям сетки.
Обозначим через В количество
узлов , лежащих внутри прямоугольника, а через Г – количество узлов на его границе. Сместим сетку на полклетки вправо и полклетки вниз. Тогда территорию прямоугольника можно «распределить» между узлами следующим образом: каждый из В узлов «контролирует» целую клетку смещённой сетки, а каждый из Г узлов – 4 граничных не угловых узла – половину клетки, а каждая из угловых точек – четверть клетки. Поэтому площадь прямоугольника S равна
S = В + + 4 · = В + -1
Слайд 9. Проверить формулу Пика для многоугольника на рисунке 1.
В = 14, Г = 8. По формуле Пика: S =
В + - 1 .S = 14 + 8/2 – 1 = 17
Ответ: 17 кв. ед.
Слайд 10Если многоугольник можно разрезать на треугольники с вершинами в узлах
сетки, то для него верна формула Пика.
Попробуйте вычислить площади многоугольников
с рисунка , используя формулу Пика. Правда ведь, легко получается!Слайд 11Глава 3. Задачи на клетчатой бумаге в контрольно-измерительных материалах ЕГЭ по
математике.
Слайд 12На клетчатой бумаге с клетками размером 1 см 1 см изображен
треугольник . Найдите его площадь в квадратных сантиметрах.
По формуле Пика:
S = В + - 1 .В = 12, Г = 6
S = 12 + 6/2 – 1 = 14 (см²)
Ответ: 14
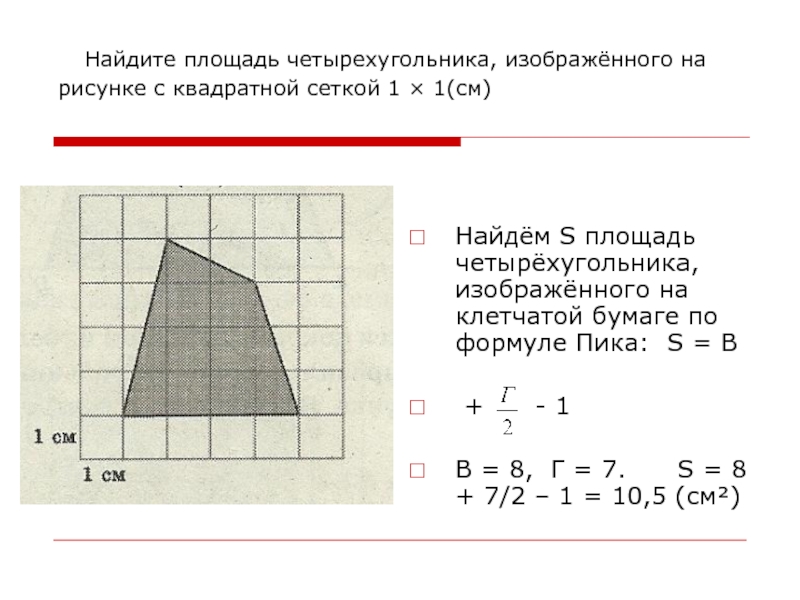
Слайд 13 Найдите площадь четырехугольника, изображённого на рисунке с квадратной сеткой
1 × 1(см)
Найдём S площадь четырёхугольника, изображённого на клетчатой
бумаге по формуле Пика: S = В+ - 1
В = 8, Г = 7. S = 8 + 7/2 – 1 = 10,5 (см²)
Слайд 14Глава 4. Заключение.
В процессе исследования рассмотрены задачи на вычисления площади
фигур, заданные на клетчатой бумаге, которые отличаются от обычных задач,
изложенных в действующих учебниках и задачниках по математике. Данная тема достаточно многогранна, задачи на клетчатой бумаге многообразны, методы и приёмы их решения также разнообразны.Слайд 15Глава 5. Библиография
Жарковская Н. М., Рисс Е. А. Геометрия клетчатой
бумаги. Формула Пика // Математика, 2009, № 17, с. 24-25.
Задачи
открытого банка заданий по математике ФИПИ.Смирнова И. М., Смирнов В. А. Геометрия на клетчатой бумаге. – М.: Чистые пруды, 2009.
Смирнова И. М., Смирнов В. А. Геометрические задачи с практическим содержанием. – М.: Чистые пруды, 2010.