Задачи на переливание. Пуассон

Содержание

1. Задачи на переливание. Пуассон
2. СоДеРжАнИе: 1.Биография Пуассона 2.Задача
3. 2. Биография ПуассонаСимеон Дени Пуассон родился
4. 3. Задача Пуассона:Один человек имеет
5. Сначала наливаете 8 литров в 8-литровый, потом
6. Решение задачи можно записать так : 8 п.5 п. 8 п.
7. Решение задачи можно записать так :5 п. 3 п.
8. Решение задачи можно записать так : 5п.12 л.9л.
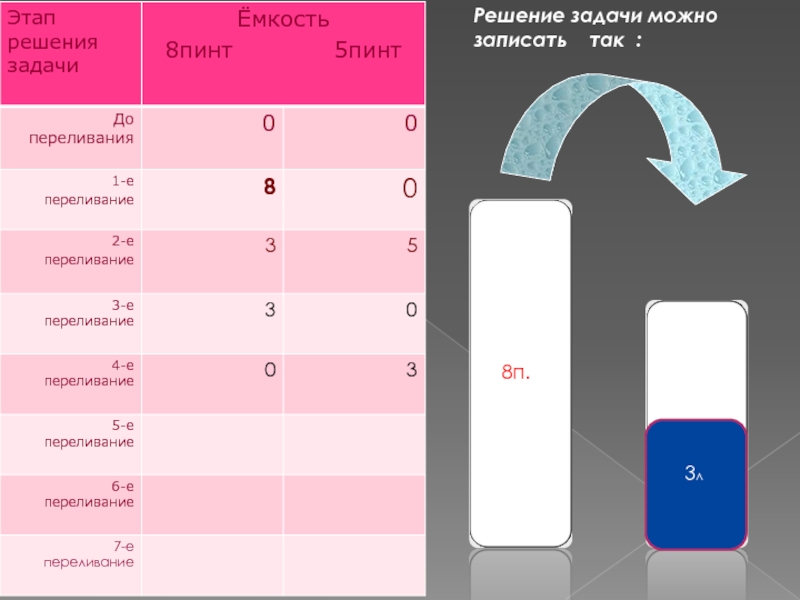
9. 3л8п.Решение задачи можно записать так :
10. 12 л.1л8п.Решение задачи можно записать так :
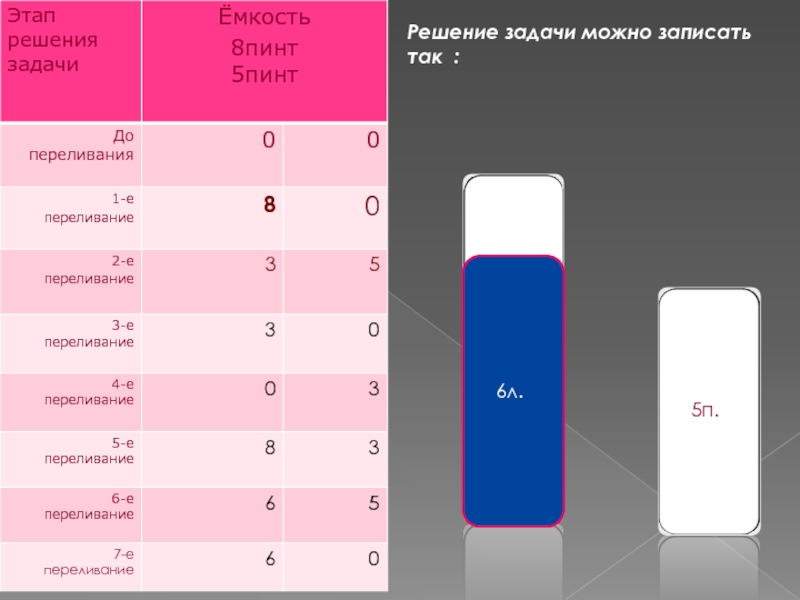
11. 6л.2л5л.8пРешение задачи можно записать так :
12. 6л.5п.Решение задачи можно записать так :
13. Подумаем над обобщением этой задачи.Пусть имеются два
14. ЗадачаВ бидоне не менее10 литров молока.Как отлить
15. Решение
16. Метод математического бильярда
17. Слайд 17
18. Слайд 18
19. Слайд 19
20. ВыводНами были рассмотрены методырешения алгебраических задач напереливание
21. СПАСИБО ЗА ВНИМАНИЕ
22. Скачать презентанцию

СоДеРжАнИе: 1.Биография Пуассона 2.Задача

Главная
Математика
Задачи на переливание. Пуассон

Слайды и текст этой презентации

Слайд 1Задачи на переливания. Пуассон.
МБОУ СОШ №2 г.Пушкино

2013 год

Слайд 2СоДеРжАнИе:
1.Биография Пуассона
2.Задача

3.Самостоятельное решение одной из задач Пуассона.
4.Ещё задачи

Слайд 3 2. Биография Пуассона

Симеон Дени Пуассон родился 21 июня 1781

года во французском городе Питивье. Его отец занимал небольшую административную

должность после службы в армии, а позже — во времена Революции — возглавил местное правительство. Будучи на этом посту, он изъявил желание помочь сыну найти себя. В 1798 году Пуассон с лучшим результатом поступил в Политехническую школу в Париже. В 1808 году Пуассон получает звание астронома в «Бюро долгот», а в 1827 году — геометром в «Бюро долгот», заменив там Лапласа. Самая древняя из задач на переливание – задача Пуассона.
Знаменитый французский математик, механик и физик Симеон Дени Пуассон (1781 – 1840) решил эту задачу в юности и впоследствии говорил, что именно она побудила его стать математиком.

2. Биография ПуассонаСимеон Дени Пуассон родился 21 июня 1781 года во французском городе Питивье. Его отец

Слайд 4 3. Задача Пуассона:
Один человек имеет в бочонке 12

пинт вина (пинта – старинная французская мера объема, 1 пинта

≈ 0,568 л) и хочет подарить половину вина, но у него нет сосуда в 6 пинт, однако имеются два пустых сосуда объемом 8 пинт и 5 пинт. Как с их помощью отлить ровно 6 пинт вина?

Решение:

3. Задача Пуассона:Один человек имеет в бочонке 12 пинт вина (пинта – старинная французская мера

Слайд 5Сначала наливаете 8 литров в 8-литровый, потом из 8- литрового

наливаете полный 5-литровый, в результате получается, что в 12-литровом -

4 литра, в 8-литровом – 3 литра, а в 5-литровом – 5 литров. Переливаете из 5-литрового в 12-литровый всю воду (или что там за жидкость), а из 8-литрового переливаете все 3 литра в 5-литровый. В результате 9 литров в 12-литровом, 0 литров в 8-литровом, и 3 литра в 5-литровом. Переливаете из 12-литрового 8 литров в пустой 8-литровый, и в 12-литровом остается 1 литр. Из 8-литрового доливаете в 5-литровый, пока 5-литровый не станет полным, (в 5-литровом было 3 литра, следовательно долили мы еще 2 литра из 8-литрового) Тогда в 8-литровом как раз остается 6 литров.

Сначала наливаете 8 литров в 8-литровый, потом из 8- литрового наливаете полный 5-литровый, в результате получается, что

Слайд 6Решение задачи можно записать так :
8 п.
5 п.

8 п.

Решение задачи можно записать так : 8 п.5 п. 8 п.

Слайд 7Решение задачи можно записать так :

5 п.
3

Решение задачи можно записать так :5 п. 3 п.

Слайд 8Решение задачи можно записать так :
5п.
12 л.
9л.

Слайд 93л
8п.
Решение задачи можно записать так :

Слайд 1012 л.
1л
8п.
Решение задачи можно записать так :

Слайд 116л.
2л
5л.
8п
Решение задачи можно записать так :

Слайд 126л.
5п.
Решение задачи можно записать так :

Слайд 13Подумаем над обобщением этой задачи.
Пусть имеются два пустых сосуда объемом

a
литров и в литров и требуется набрать из реки
ровно с

литров воды. Если число с не делится на
наибольший общий делитель чисел а и в, то это
сделать невозможно.

Если с делится на наибольший общий
делитель чисел а и в, то в таком случае задача
всегда имеет решение. В частности, это всегда
возможно, если числа а и в взаимно просты.