Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Задачи на построение сечений тетраэдра и па раллелепипеда
Содержание
- 1. Задачи на построение сечений тетраэдра и па раллелепипеда
- 2. При построении сечений необходимо учитывать три факта:
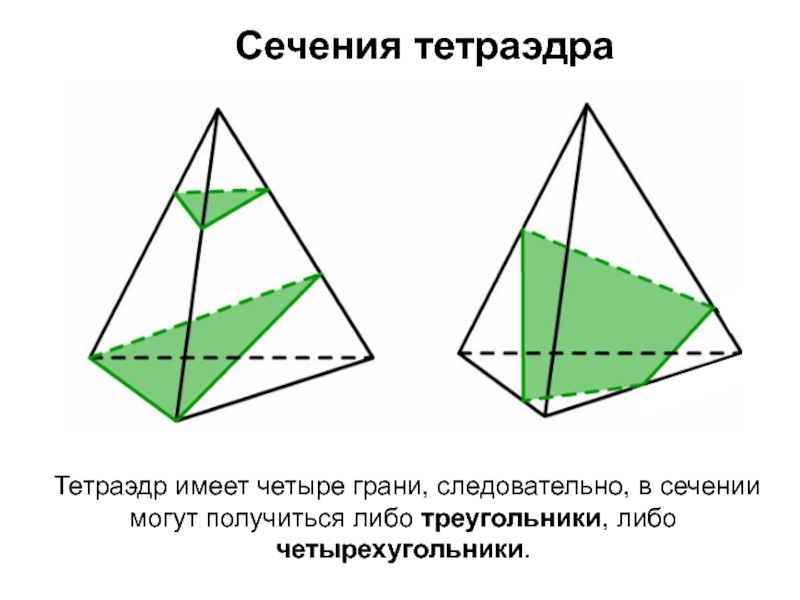
- 3. Тетраэдр имеет четыре грани, следовательно, в сечении могут получиться либо треугольники, либо четырехугольники.Сечения тетраэдра
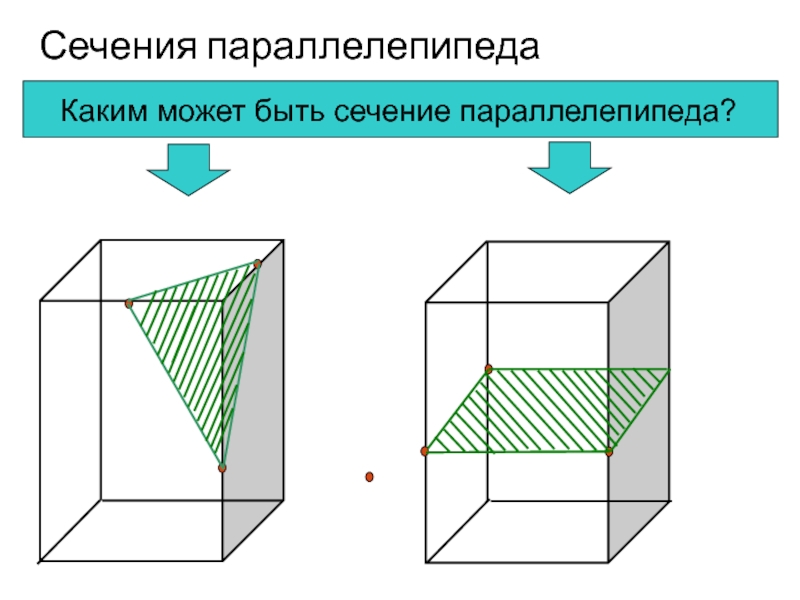
- 4. Сечения параллелепипедаКаким может быть сечение параллелепипеда?
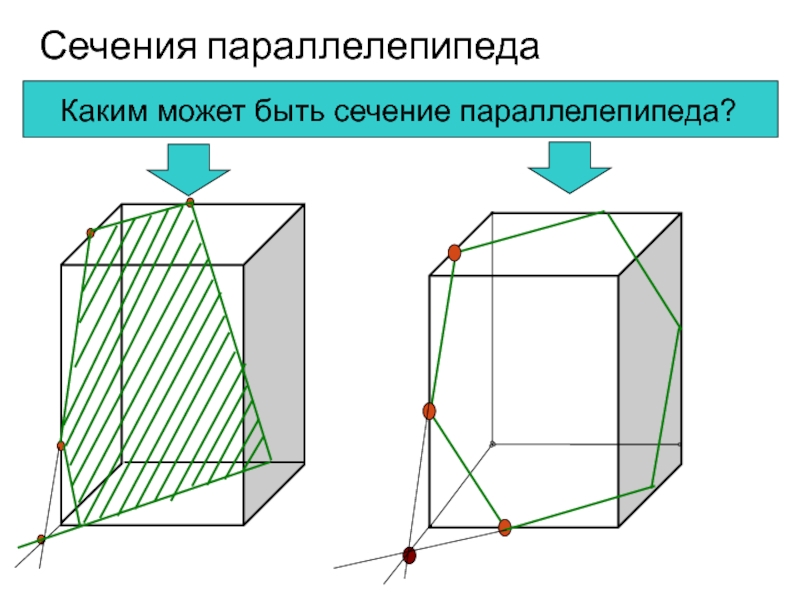
- 5. Сечения параллелепипедаКаким может быть сечение параллелепипеда?
- 6. 1. Через точку М параллельно плоскости (АДС).АДСВМ
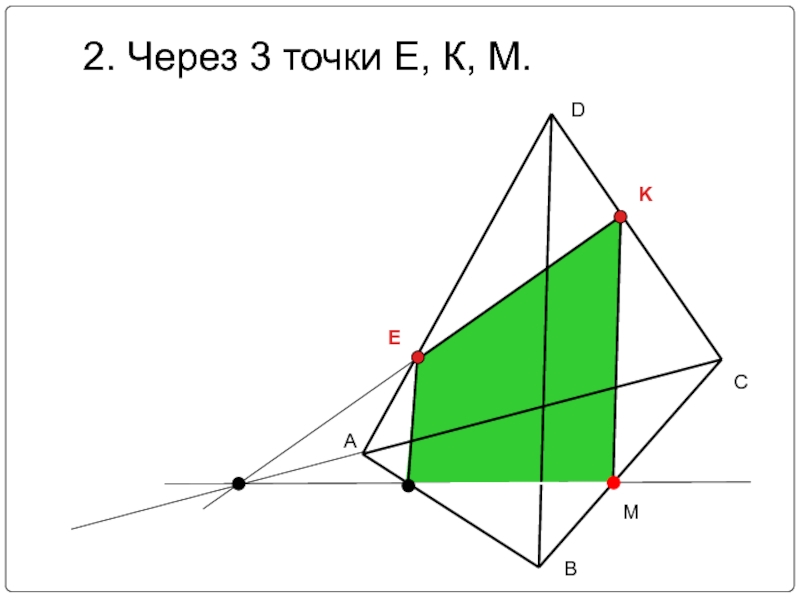
- 7. АСВDEKM2. Через 3 точки Е, К, М.
- 8. 3. Через три точки M, N, P.NМР
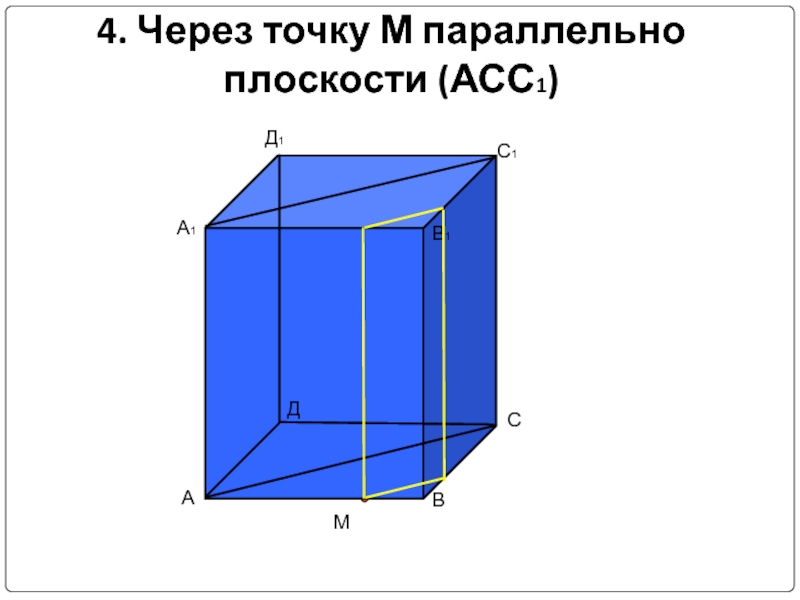
- 9. 4. Через точку М параллельно плоскости (АСС1)М
- 10. Домашнее заданиеп. 14 №72, 80 или №83(а), 84
- 11. Скачать презентанцию
При построении сечений необходимо учитывать три факта: Если секущая плоскость пересекает параллельные плоскости, то линии их пересечения параллельныЕсли даны 2 точки в одной плоскости, то через них можно провести прямую. (акс.
Слайды и текст этой презентации
Слайд 2При построении сечений необходимо учитывать три факта:
Если секущая плоскость
пересекает параллельные плоскости, то линии их пересечения параллельны
Если даны 2
точки в одной плоскости, то через них можно провести прямую. (акс. А-2)Находим пересекающиеся прямые одной плоскости и строим точку их пересечения
Слайд 3
Тетраэдр имеет четыре грани, следовательно, в сечении могут получиться либо
треугольники, либо четырехугольники.
Сечения тетраэдра
