Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Задачи на разрезание
Содержание
- 1. Задачи на разрезание
- 2. Основная цель:познакомить учащихся с задачами на разрезание;развитие пространственного представления и логического мышления, интуиции и смекалки.
- 3. Основное содержание Историческая справка.Разновидности задач на разрезание.Геометрические софизмы и занимательные задачи.
- 4. Задачи на разрезание и перекраивание возникли в
- 5. Разновидности задач на разрезаниеЗадачи, которые являются
- 6. ОПРЕДЕЛЕНИЯРавновеликие фигуры – плоские фигуры, имеющие равные
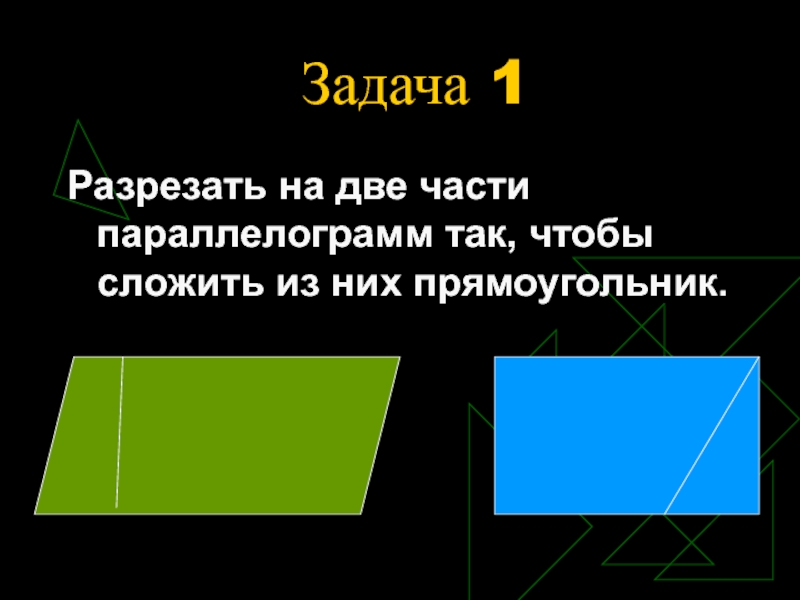
- 7. Задача 1Разрезать на две части параллелограмм так, чтобы сложить из них прямоугольник.
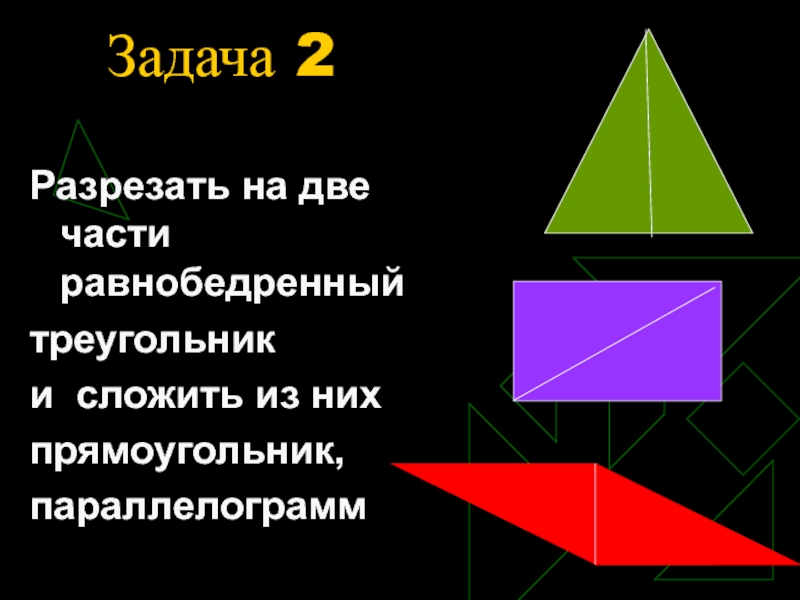
- 8. Задача 2Разрезать на две части равнобедренный треугольник и сложить из них прямоугольник,параллелограмм
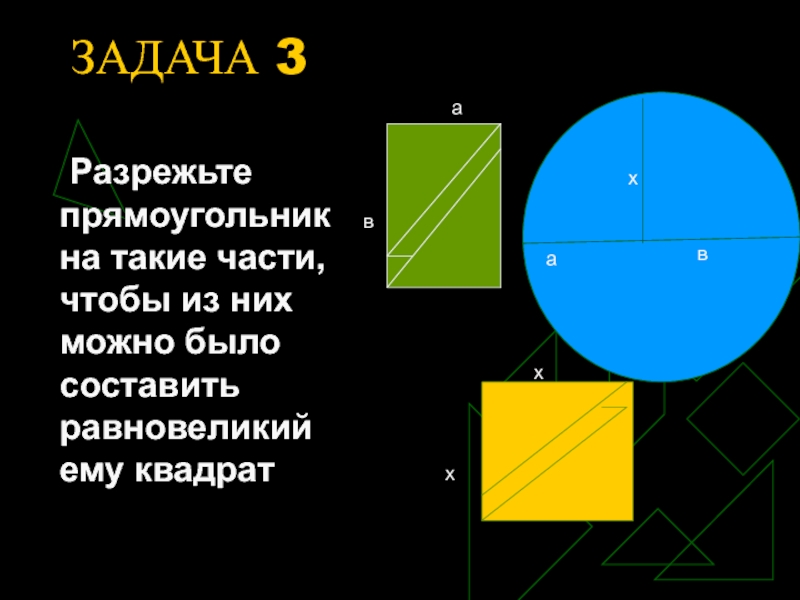
- 9. ЗАДАЧА 3 Разрежьте прямоугольник на такие части, чтобы из них можно было составить равновеликий ему квадратававххх
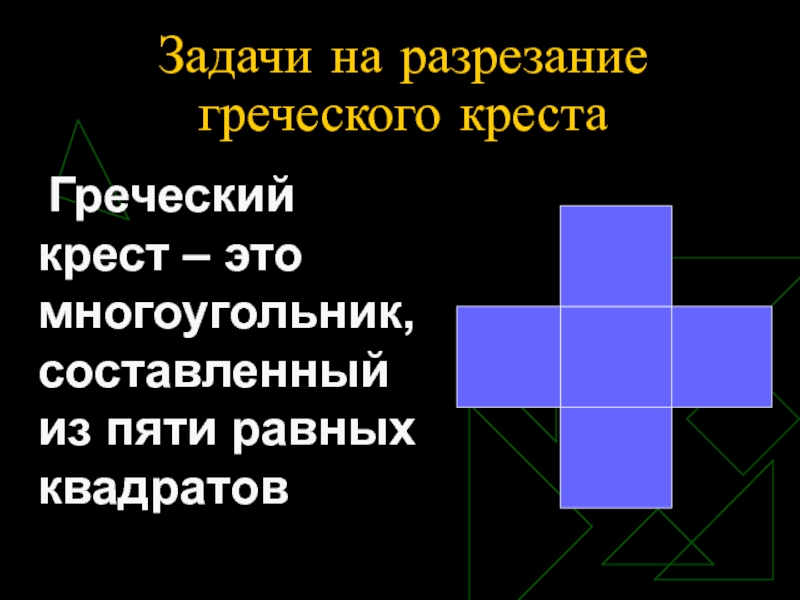
- 10. Задачи на разрезание греческого креста Греческий крест – это многоугольник, составленный из пяти равных квадратов
- 11. ЗАДАЧА 4 Разрежьте греческий крест на такие части, чтобы из них можно было составить равновеликий ему квадрат.
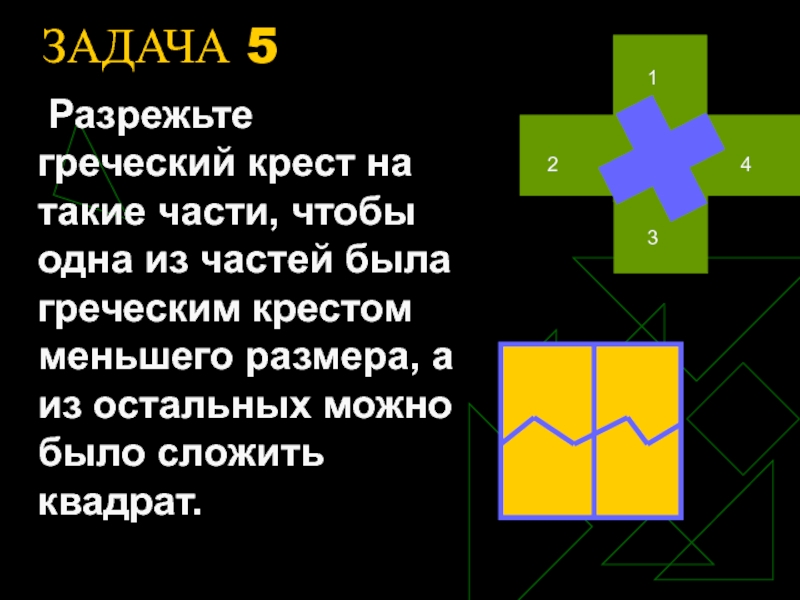
- 12. ЗАДАЧА 5 Разрежьте греческий крест на такие части,
- 13. Геометрические софизмы и занимательные задачи. Софизм
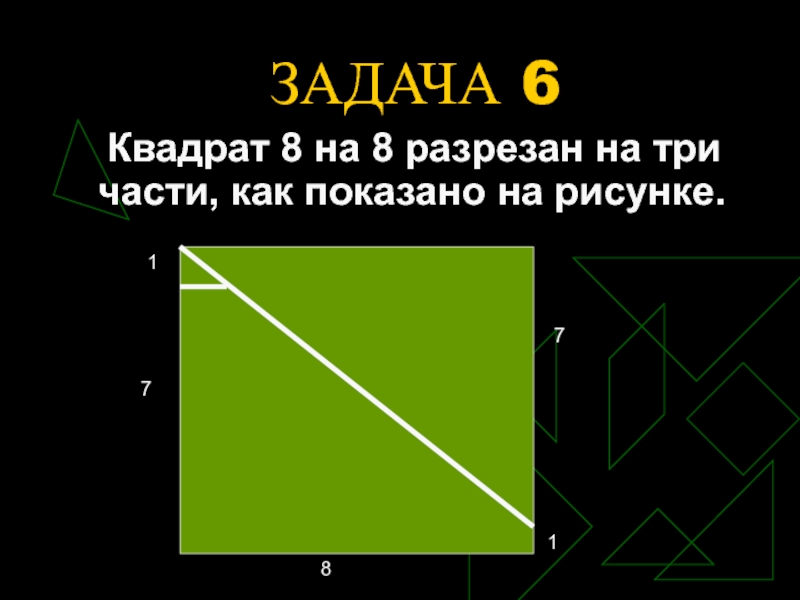
- 14. ЗАДАЧА 6 Квадрат 8 на 8 разрезан на три части, как показано на рисунке.
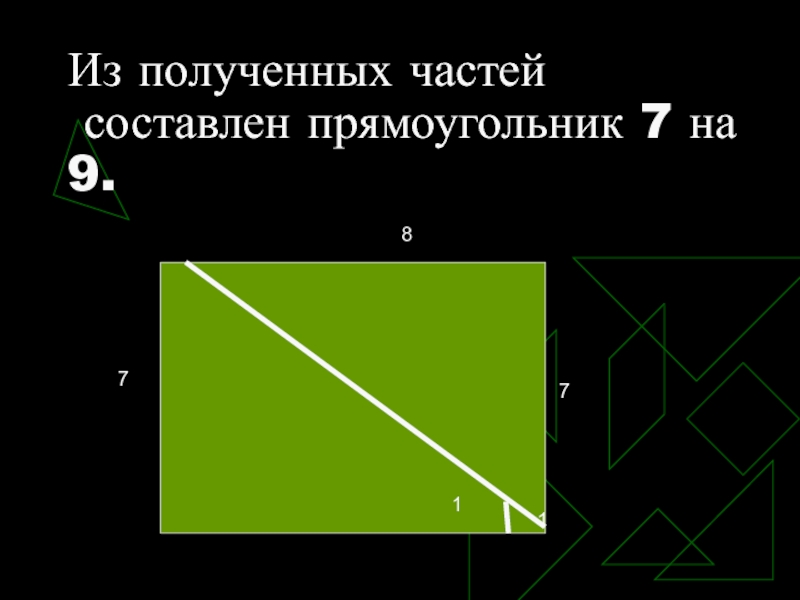
- 15. Из полученных частей составлен прямоугольник 7 на 9.
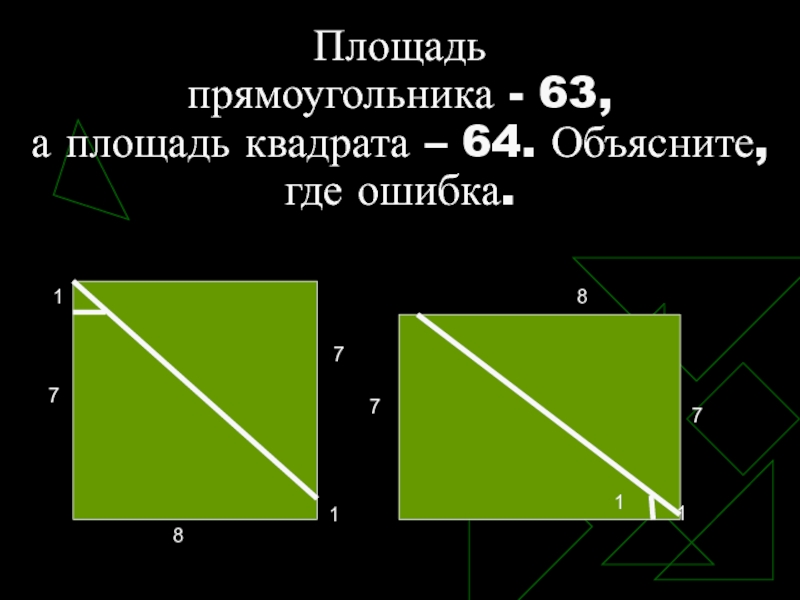
- 16. Площадь прямоугольника - 63, а площадь квадрата – 64. Объясните, где ошибка.
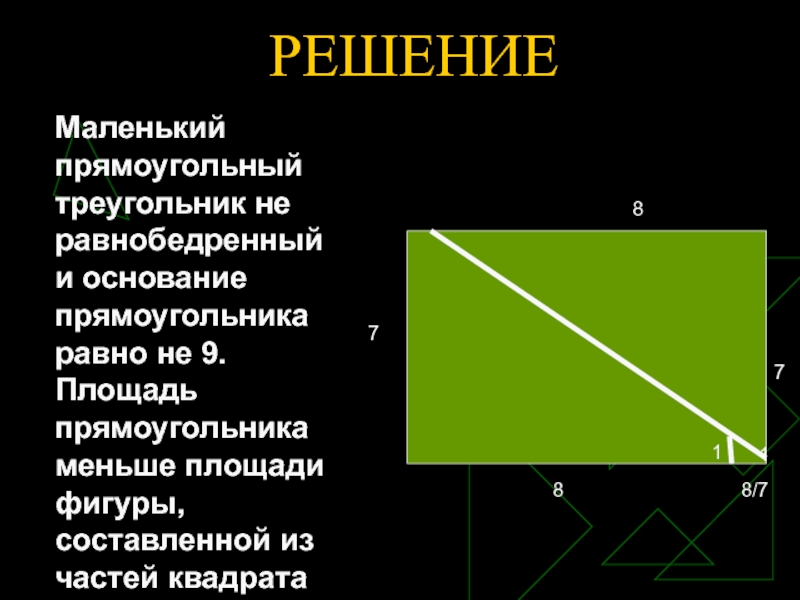
- 17. РЕШЕНИЕМаленький прямоугольный треугольник не равнобедренный и основание
- 18. ЛитератураДьюдени Г. Э. 520 головоломок // Сост.
- 19. Скачать презентанцию
Основная цель:познакомить учащихся с задачами на разрезание;развитие пространственного представления и логического мышления, интуиции и смекалки.
Слайды и текст этой презентации
Слайд 2Основная цель:
познакомить учащихся с задачами на разрезание;
развитие пространственного представления и
логического мышления, интуиции и смекалки.
Слайд 3Основное содержание
Историческая справка.
Разновидности задач на
разрезание.
Геометрические софизмы и занимательные задачи.
Слайд 4Задачи на разрезание и перекраивание возникли в глубокой древности:
VII – V вв. до н. э. в Индии в
книге «Правила веревки»II в. до н. э. в «Началах» Евклида
1832 – 1833 гг. теорема Больяи – Гервина (равновеликие многоугольники являются равносоставленными)
XX в. Генри Э. Дьюдени и Гарри Линдгрен – классики занимательной геометрии
ИСТОРИЧЕСКАЯ СПРАВКА
Слайд 5Разновидности
задач на разрезание
Задачи, которые являются составляющими вывода формул площадей
параллелограмма, треугольника, трапеции
Задачи на разрезание греческого креста
Задачи на перекраивание двух
фигур в равновеликую им третью фигуруСлайд 6ОПРЕДЕЛЕНИЯ
Равновеликие фигуры – плоские фигуры, имеющие равные площади
Равносоставленные фигуры –
это фигуры, которые можно разрезать на одинаковое число соответственно равных
частейСлайд 8Задача 2
Разрезать на две части равнобедренный
треугольник
и сложить из
них
прямоугольник,
параллелограмм
Слайд 9ЗАДАЧА 3
Разрежьте прямоугольник на такие части, чтобы из них можно
было составить равновеликий ему квадрат
а
в
а
в
х
х
х
Слайд 10Задачи на разрезание греческого креста
Греческий крест – это многоугольник, составленный
из пяти равных квадратов
Слайд 11ЗАДАЧА 4
Разрежьте греческий крест на такие части, чтобы из них
можно было составить равновеликий ему квадрат.
Слайд 12ЗАДАЧА 5
Разрежьте греческий крест на такие части, чтобы одна из
частей была греческим крестом меньшего размера, а из остальных можно
было сложить квадрат.Слайд 13
Геометрические софизмы и занимательные задачи.
Софизм - рассуждение, обосновывающее заведомую нелепость,
абсурд или парадоксальное утверждение.
Геометрический софизм – ошибочный чертеж или кажущиеся
«очевидности».Слайд 17РЕШЕНИЕ
Маленький прямоугольный треугольник не равнобедренный и основание прямоугольника равно не
9. Площадь прямоугольника меньше площади фигуры, составленной из частей квадрата
Слайд 18
Литература
Дьюдени Г. Э. 520 головоломок // Сост. и ред. амер.
изд. М. Гарднер. Пер. с анг.
Ю. Н.
Сударева. – М.: Мир, 1975 .2. Екимова М. А. Кукин Г. П. Задачи на разрезание. М.: МЦНМО, 2002.
3. Игнатьев Е. И. В царстве смекалки. М.: Наука, 1978.
4. Лигрен Г. Занимательные задачи на разрезание / Пер. с анг. Ю. Н. Сударева. Под ред. и послесл. И. М. Яглома. – М.: Мир,1977.