Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Защита проекта "Арифметическая и геометрическая прогрессии"
Содержание
- 1. Защита проекта "Арифметическая и геометрическая прогрессии"
- 2. Я увлекаюсь биологией.Цель исследования: выяснить применимость формул арифметической и геометрической прогрессий к биологическим явлениям.
- 3. СодержаниеТеоретическое обоснование Формулы арифметической прогрессии Формулы геометрической прогрессииПрогрессии в
- 4. Слайд 4
- 5. Арифметическая прогрессия -числовая последовательность видaа1, а1+d, a1 +2d,…,a1+(n-2)d,
- 6. Формула члена арифметической прогрессии
- 7. Сумма первых n членов арифметической прогрессии Сумма первых n членов
- 8. Арифметические прогрессии высших порядков
- 9. Геометрическая прогрессия — последовательность чисел b1, b2,
- 10. Формула члена геометрической прогрессии
- 11. Сумма первых n членов геометрической прогрессии
- 12. Все живые существа рождаются, растут,
- 13. Прогрессии в природе. Прогрессия среди млекопитающих и
- 14. Числовые данные семейства медвежьих (рост, ношение детеныша,
- 15. Числовые данные отряда совообразных (длина, период высиживания,
- 16. Слайд 16
- 17. Быстрое размножение бактерий Если одну
- 18. Размножение одуванчика Одуванчик приносит ежегодно около
- 19. Размножение в геометрической прогрессии В конце XVIII
- 20. Размножение в геометрической прогрессииНа острове Ямайке водились
- 21. Размножение в геометрической прогрессииИзвестно, что врагом крыс
- 22. Вывод Через поиск информации в различных источниках, наблюдение
- 23. Слайд 23
- 24. Спасибо за внимание!
- 25. Скачать презентанцию
Я увлекаюсь биологией.Цель исследования: выяснить применимость формул арифметической и геометрической прогрессий к биологическим явлениям.
Слайды и текст этой презентации
Слайд 1Арифметическая и геометрическая прогрессии в ПРИРОДЕ
Составила:
Александра Юнина, 9 класс
ЧОУ
СОШ «Исток».
Слайд 2Я увлекаюсь биологией.
Цель исследования: выяснить применимость формул арифметической и геометрической
прогрессий к биологическим явлениям.
Слайд 3Содержание
Теоретическое обоснование
Формулы арифметической прогрессии
Формулы геометрической прогрессии
Прогрессии в природе на примере
млекопитающих и пернатых
Прогрессии в природе на примере бактерий и растений
Размножение
в геометрической прогрессииВывод
Слайд 5Арифметическая прогрессия
-числовая последовательность видa
а1, а1+d, a1 +2d,…,a1+(n-2)d, a1+(n-1)d,…
то есть последовательность чисел (членов прогрессии), в которой каждое число, начиная
со второго, получается из предыдущего добавлением к нему постоянного числа - разности прогрессии(d):an=an-1+d
Слайд 6Формула члена арифметической прогрессии
Член
арифметической прогрессии с номером n может быть найден по формуле
an=a1+(n-1)d
где a1 —первый член прогрессии, d — её разность.Характеристическое свойство арифметической прогрессии
Последовательность а1,a2,a3,… есть арифметическая прогрессия, для ее элементов выполняется условие
Слайд 7Сумма первых n членов арифметической прогрессии
Сумма первых n членов арифметической прогрессии
Sn=a1+a2+a3+…+an
может быть найдена по формулам
где (1): a1 — первый
член прогрессии, d— разность прогрессии, n— количество суммируемых членов.(2): a1 — первый член прогрессии,an — член с номером n, n— количество суммируемых членов.
Слайд 8Арифметические прогрессии высших порядков
Арифметической прогрессией второго
порядка называется такая последовательность чисел:
0, 1, 4, 9, 16, 25,
36…,разности которых образуют простую арифметическую прогрессию с разностью 2:
1, 3, 5, 7, 9, 11…
Слайд 9Геометрическая прогрессия
— последовательность чисел
b1, b2, b3,… (членов прогрессии),
в которой каждое
последующее число, начиная со второго, получается из предыдущего умножением его
на определённое число q (знаменатель прогрессии), где b1≠0, q≠0:b1, b2=b1*q, b3= b2*q,… bn=bn-1*q
Слайд 10Формула члена геометрической прогрессии
Любой член
геометрической прогрессии может быть вычислен по формуле:
bn=b1*qn-1
где b1-первый член прогрессии, q-её знаменатель.Характеристическое свойство геометрической прогрессии
Последовательность b1,b2,b3,… есть геометрическая прогрессия, для ее элементов выполняется условие
Слайд 11Сумма первых n членов геометрической прогрессии
Сумма первых n
членов геометрической прогрессии
Sn=b1+b2+b3+…+bn может быть найдена по формуле
где b1 –первый член прогрессии, q- знаменатель прогрессии, n-количество суммированных членов.Слайд 12 Все живые существа рождаются, растут, изменяются, стареют, умирают.
Некоторые из этих процессов подчинены законам числовой последовательности.
Слайд 13Прогрессии в природе.
Прогрессия среди млекопитающих и пернатых
В природе не существует хаоса, все тесно взаимосвязано законами, правилами,
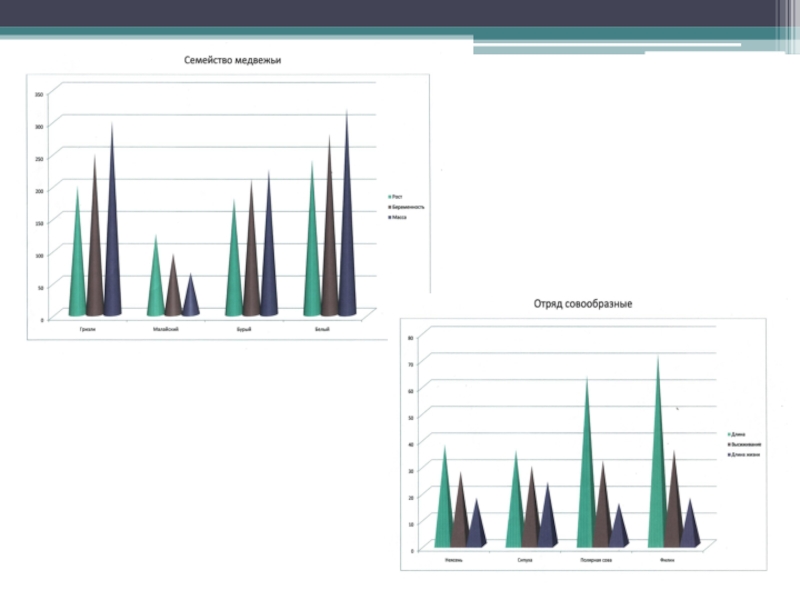
формулами Слайд 14Числовые данные семейства медвежьих (рост, ношение детеныша, масса)
Медведь гризли
рост
200 см,
ношение детеныша 250дней,
масса 300 кг.
Числа 200,
250, 300 составляют арифметическую прогрессию с разностью равной 50. (d=50)*.Малайский медведь
рост 125 см,
ношение детеныша 95 дней,
масса 65 кг.
Числа 65, 95, 125 -арифметическая прогрессия,
где d= 30
Бурый медведь
рост 180 см,
ношение детеныша 200 дней,
масса 220 кг.
Числа 180, 200, 220 –арифметическая прогрессия,
где d=20.
Белый медведь (самка)
рост 240 см,
ношение детеныша 280 дней,
масса 320 кг.
Числа 240, 280, 320 – арифметическая прогрессия,
где d=40.
*Есть небольшие отклонения d, но они незначительны
Слайд 15Числовые данные отряда совообразных (длина, период высиживания, продолжительность жизни)
Неясень
Длина 38
Период
высиживания 28
Продолжительность жизни 18
Числа 38, 28, 18 –арифметическая
прогрессия,где d= 10
Сипуха
Длина 36
Период высиживания 30
Продолжительность жизни 24
Числа 36, 30, 24 – арифметическая прогрессия,
где d = 6
Полярная сова
Длина 64
Период высиживания 32
Продолжительность жизни 16
Числа 64, 32, 16 – геометрическая прогрессия,
где q=0.5
Филин
Длина 72
Период высиживания 36
Продолжительность жизни 18
Числа 72, 36, 18 – геометрическая прогрессия,
где q=0.5
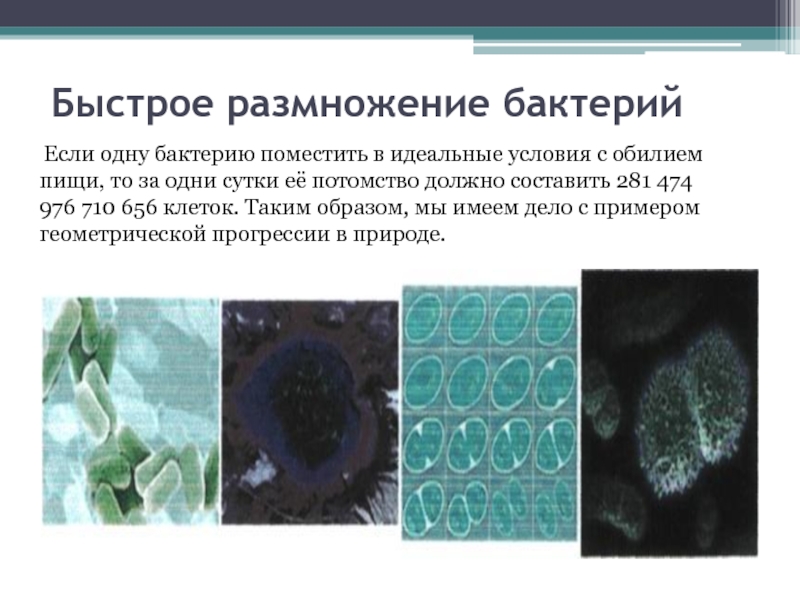
Слайд 17Быстрое размножение бактерий
Если одну бактерию поместить в
идеальные условия с обилием пищи, то за одни сутки её
потомство должно составить 281 474 976 710 656 клеток. Таким образом, мы имеем дело с примером геометрической прогрессии в природе.Слайд 18
Размножение одуванчика
Одуванчик приносит ежегодно около 100 семянок. Если бы все
они прорастали, мы имели бы: в 1 год 1 растение
в 2 года 100 растений в 3 года 10000 растений в 4 года 1000000 растений в 5 года 100000000 растений в 6 года 10000000000 растений в 7 года 1000000000000 растений в 8 года 100000000000000 растений в 9 года 10000000000000000 растений(В одной головке одуванчика было насчитано даже около 200 семянок.)
Это в 70 раз больше, чем имеется квадратных метров на всей суше. Следовательно, на 9-м году материки земного шара были бы покрыты одуванчиками, по 70 на каждом квадратном метре.
Почему же в действительности не наблюдаем мы такого чудовищно быстрого размножения? Потому, что огромное большинство семян погибает, не давая ростков: они или не попадают на подходящую почву и вовсе не прорастают, или, начав прорастать, заглушаются другими растениями, или же, наконец, просто истребляются животными.
Размножение одуванчика происходит в геометрической прогрессии.
Слайд 19Размножение в геометрической прогрессии
В конце XVIII века в Австралию
был ввезен кролик, и так как там отсутствуют хищники, питающиеся
кроликами, то размножение этих грызунов пошло необычайно быстрым темпом. Вскоре полчища кроликов наводнили всю Австралию, нанося страшный вред сельскому хозяйству и превратившись в подлинное бедствие. На борьбу с этим бичом сельского хозяйства брошены были огромные средства, и только благодаря энергичным мерам удалось справиться с бедой. Приблизительно то же самое повторилось поздней с кроликами в Калифорнии.Слайд 20Размножение в геометрической прогрессии
На острове Ямайке водились в изобилии ядовитые
змеи.
Чтобы от них избавиться, решено было ввезти на остров
птицу-секретаря, яростного истребителя ядовитых змей. Число змей действительно вскоре уменьшилось, зато необычайно расплодились полевые крысы, раньше поедавшиеся змеями.
Крысы приносили такой ущерб плантациям сахарного тростника, что пришлось серьезно подумать об их истреблении.
Слайд 21Размножение в геометрической прогрессии
Известно, что врагом крыс является индийский мангуст.
Решено было привести на остров 4 пары этих животных и
предоставить им свободно размножаться. Не прошло и десяти лет, как мангусты уничтожили на нем крыс.Однако истребив крыс, мангусты стали питаться чем попало, сделавшись всеядными животными: нападали на щенят, козлят, поросят, домашних птиц и их яйца.
Затем принялись за плодовые сады, хлебные поля, плантации. Жители приступили к уничтожению своих недавних союзников, но им удалось лишь до некоторой степени ограничить приносимый мангустами вред.