Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Депозит. Кредит. Проценты. Дисконтирование
Содержание
- 1. Депозит. Кредит. Проценты. Дисконтирование
- 2. План урокаЧто такое депозит?Как считать доход по
- 3. Депозит (банковский вклад)Банковский вклад (или банковский депозит)
- 4. Научимся считать сколько денег будет на нашем депозитном счете при определенных условиях
- 5. Депозит. Задача. Условие.Вкладчик положил в банк 100
- 6. Депозит. Задача. Решение.100 000 рублей это сумма,
- 7. Депозит. Задача. Решение.10% это то, что ранее
- 8. Депозит. Задача. Решение.1 год это срок вклада.
- 9. Депозит. Задача. Решение.Последовательность решения:Сколько будет 10% от
- 10. Депозит. Задача. Решение.Распишем решение вынеся 100000 за
- 11. Депозит. Задача 2. Условие и решение.Вкладчик положил
- 12. Деньги сегодня и завтраВопрос: что вы предпочтете
- 13. Деньги сегодня и завтраДавайте применим знания о
- 14. Деньги сегодня и завтраСамое интересное, что можно
- 15. Деньги сегодня и завтраВот так мы и
- 16. Деньги сегодня и завтраPV – present value
- 17. Так уж ли сложен «сложный процент»?Давайте усложним
- 18. Так уж ли сложен «сложный процент»?Через 1
- 19. Так уж ли сложен «сложный процент»?Обратите внимание,
- 20. Так уж ли сложен «сложный процент»?Наш расчет
- 21. Так уж ли сложен «сложный процент»?Давайте подставим
- 22. Так уж ли сложен «сложный процент»?Мы почти
- 23. Так уж ли сложен «сложный процент»?Давайте теперь
- 24. Давайте попрактикуемсяНайдите сколько будет денег на вашем
- 25. КредитКредит - это передача во временное пользование
- 26. Научимся считать сколько денег мы будем должны кредитору при определенных условиях кредитования
- 27. Кредит. Задача. Условие.Заемщик взял в банке 10000
- 28. Кредит. Задача. Условие.Давайте вспомним нашу старую задачу
- 29. Кредит. Задача. Решение.Заемщик взял в банке 10000
- 30. Кредит. Задача 2. Условие. Решение.Заемщик взял в
- 31. Кредит. Задача 2. Условие. Решение.И мы опять
- 32. Кредит. Задача 3. Условие.Заемщик взял в банке
- 33. АннуитетАннуитет это погашение кредита равномерными (одинаковыми) платежами
- 34. Аннуитет. Формула.Приведем формулу для так называемого коэффициента
- 35. Кредит. Задача 3. Решение.Напомним условие задачи.Заемщик взял
- 36. Кредит. Задача 3. Решение.Теперь у нас есть
- 37. Кредит. Задача 3. Решение.C – процент по
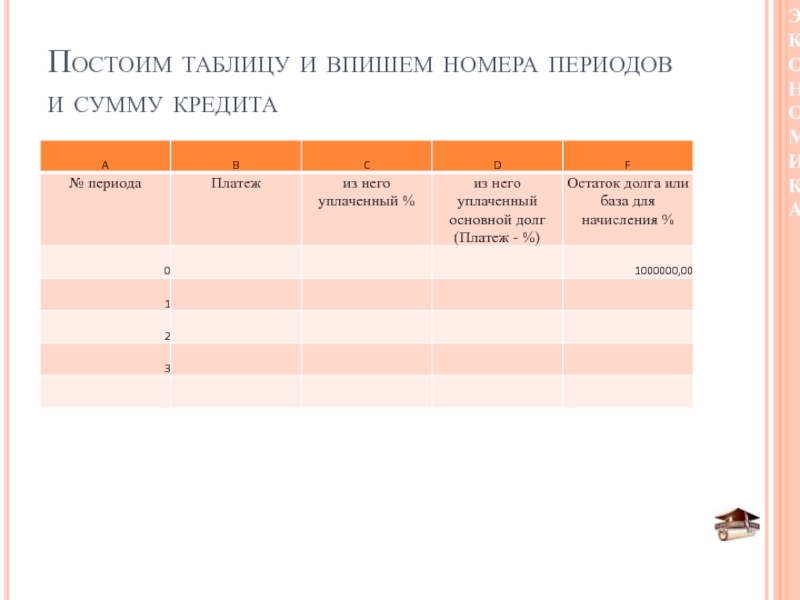
- 38. Постоим таблицу и впишем номера периодов и сумму кредита
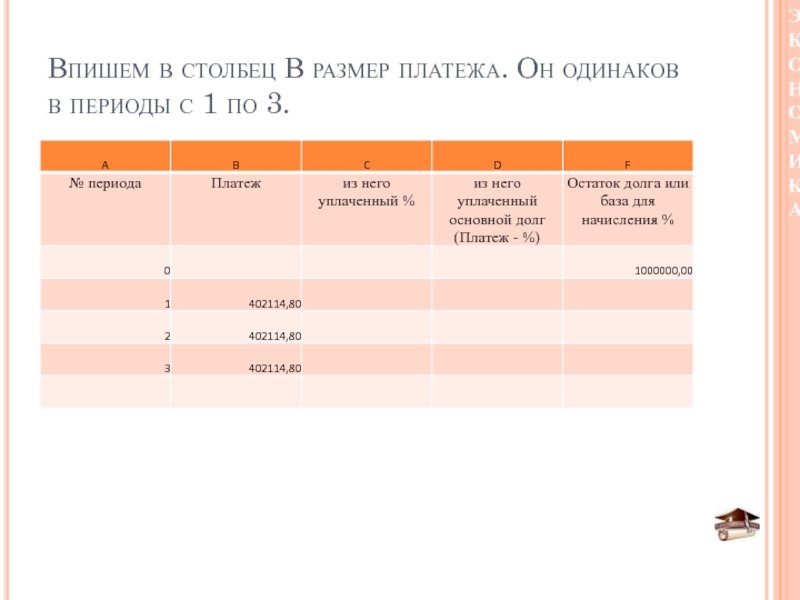
- 39. Впишем в столбец В размер платежа. Он одинаков в периоды с 1 по 3.
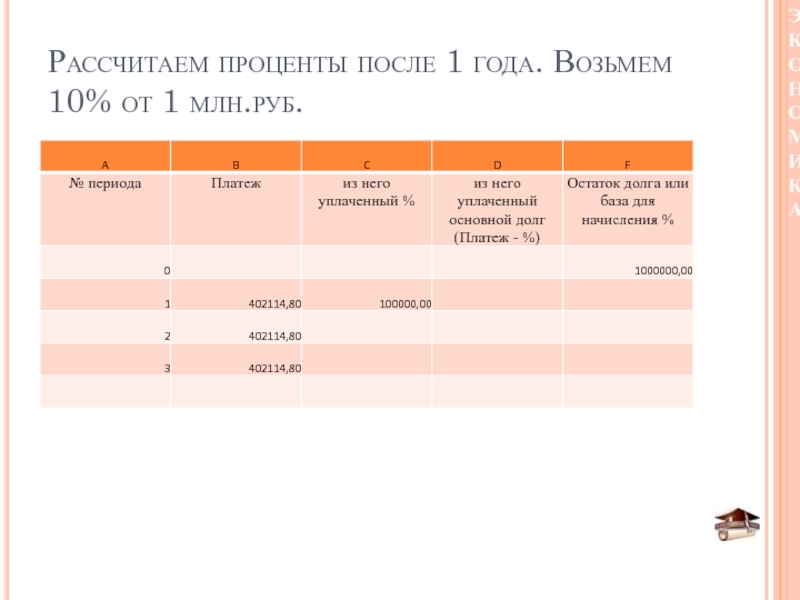
- 40. Рассчитаем проценты после 1 года. Возьмем 10% от 1 млн.руб.
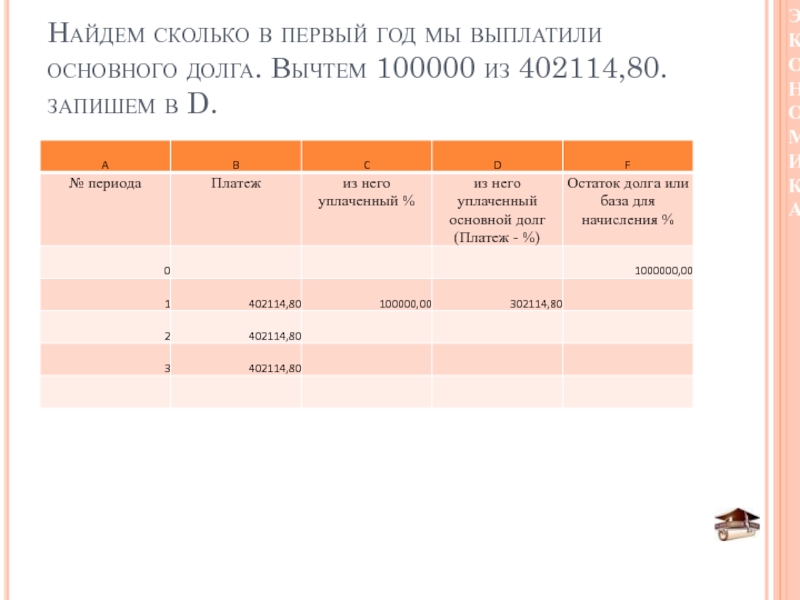
- 41. Найдем сколько в первый год мы выплатили основного долга. Вычтем 100000 из 402114,80. запишем в D.
- 42. Узнаем сколько нам осталось погасить кредита. Вычтем 302114,80 из 1 млн. руб. запишем в столбец F.
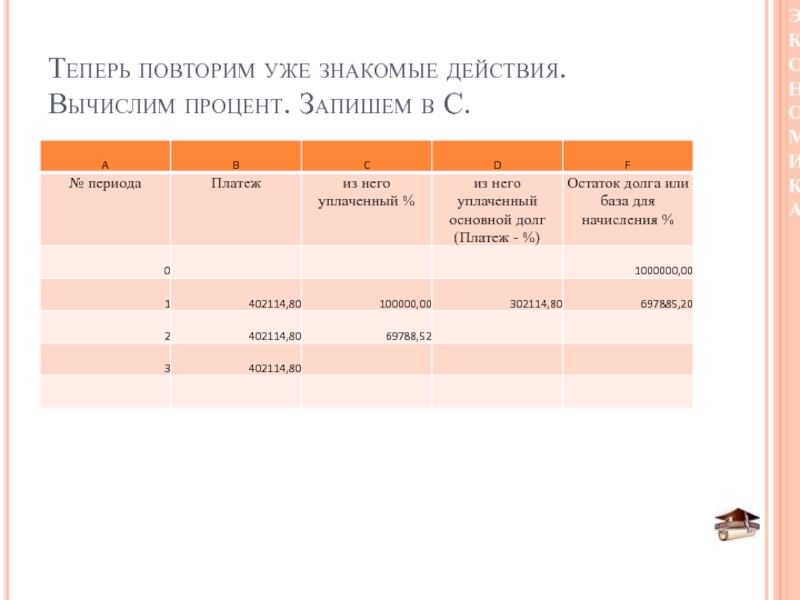
- 43. Теперь повторим уже знакомые действия. Вычислим процент. Запишем в С.
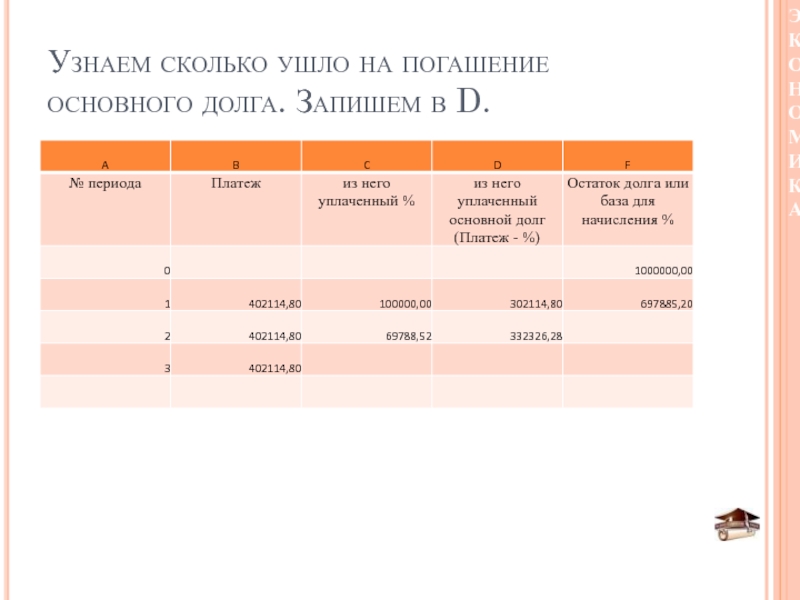
- 44. Узнаем сколько ушло на погашение основного долга. Запишем в D.
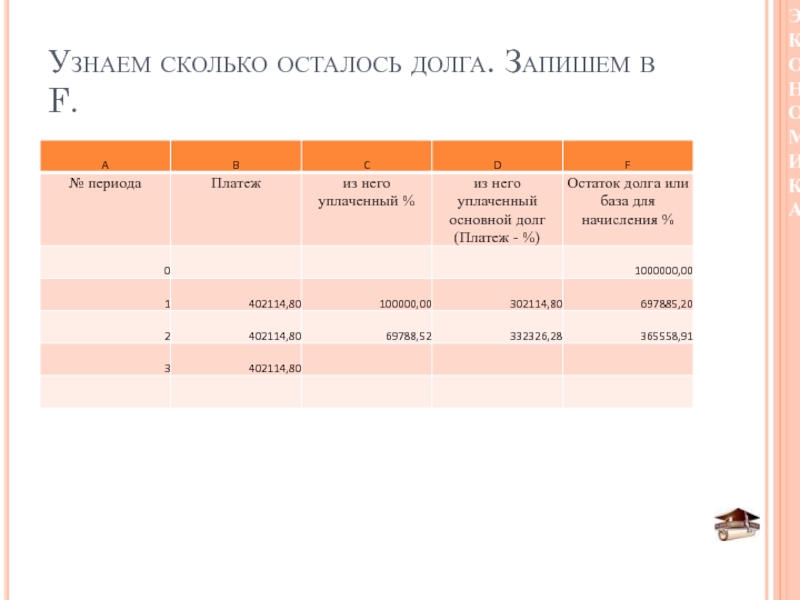
- 45. Узнаем сколько осталось долга. Запишем в F.
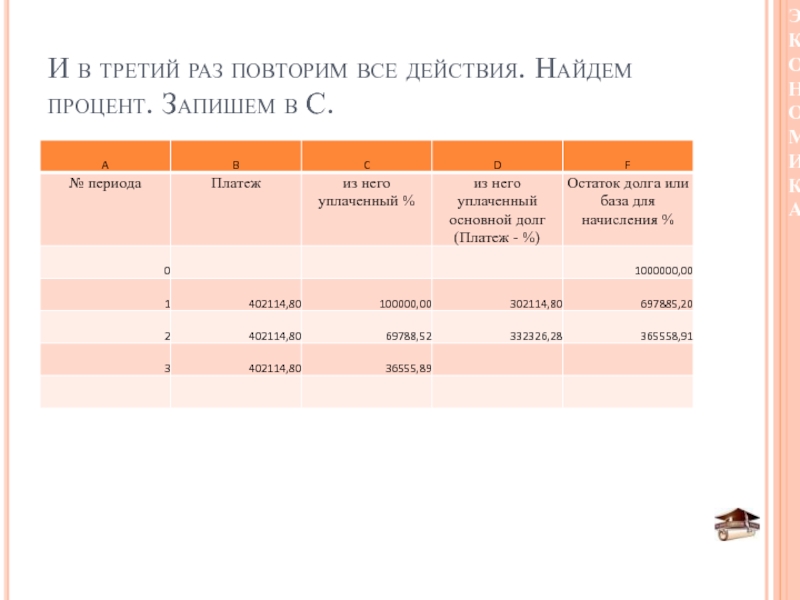
- 46. И в третий раз повторим все действия. Найдем процент. Запишем в С.
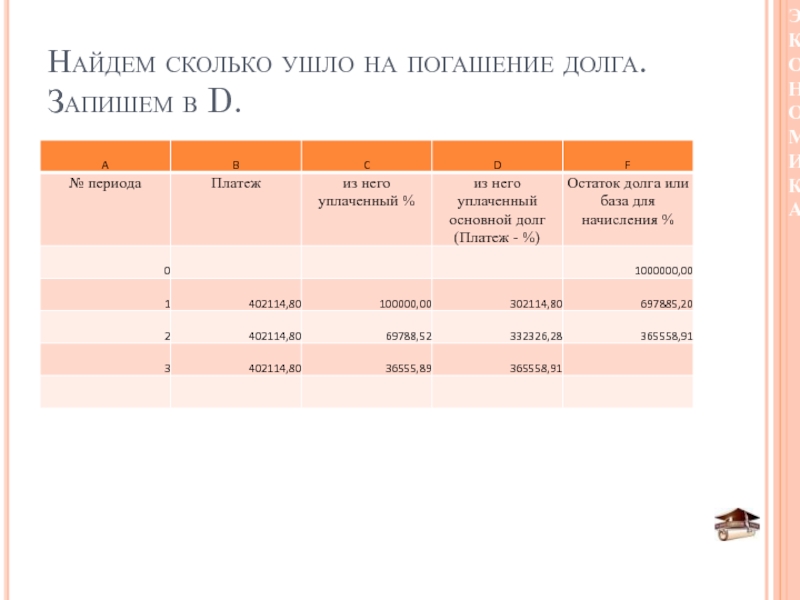
- 47. Найдем сколько ушло на погашение долга. Запишем в D.
- 48. И теперь самая интересная часть. Вычтем последнее
- 49. Сумма по D оказалась равной размеру кредита,
- 50. Задание на урокеСоставить расписание погашения кредита если
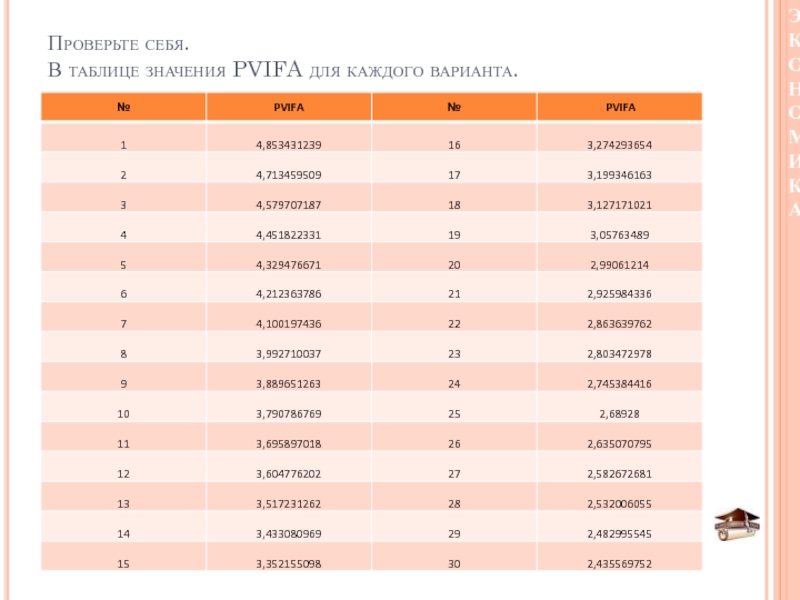
- 51. Проверьте себя. В таблице значения PVIFA для каждого варианта.
- 52. Все молодцы! Урок закончен.
- 53. список использованных печатных источников1. Экономика. (Основы экономической
- 54. активные ссылки на страницы материалов в Интернете
- 55. активные ссылки на использованные изображения Изображение «восклицательного
- 56. Скачать презентанцию
План урокаЧто такое депозит?Как считать доход по депозиту?Как считать сложные проценты?Что такое кредит?Как считать задолженность по кредиту?Что такое аннуитет?Как составлять график погашения кредита?
Слайды и текст этой презентации
Слайд 1Депозит, кредит, процент, дисконтирование
Учитель экономики
МАОУ «Самарского медико-технического лицея» г.о.
Самара
Слайд 2План урока
Что такое депозит?
Как считать доход по депозиту?
Как считать сложные
проценты?
Что такое кредит?
Как считать задолженность по кредиту?
Что такое аннуитет?
Как составлять
график погашения кредита?Слайд 3Депозит (банковский вклад)
Банковский вклад (или банковский депозит) — сумма денег,
переданная лицом кредитному учреждению с целью получить доход в виде
процентов, образующихся в ходе финансовых операций с вкладом.Слайд 5Депозит. Задача. Условие.
Вкладчик положил в банк 100 000 рублей под
10% годовых на 1 год.
Сколько денег будет на счете вкладчика
через 1 год?Разберемся с числами. Что они означают?
Слайд 6Депозит. Задача. Решение.
100 000 рублей это сумма, которую вкладчик приносит
в банк, отдает кассиру, который зачисляет эту сумму на счет
вкладчика (мы не рассматриваем детали данной операции).Слайд 7Депозит. Задача. Решение.
10% это то, что ранее в русском языке
называлось «интерес». Зачем люди относят деньги в банк? В частности,
чтобы заработать. 10% и будет «заработок» вкладчика.Т.е. сумма вклада увеличится на 10% через оговоренное время.
Т.е. на вкладе будет лежать денег больше, чем было изначально. На 10% больше.
Слайд 8Депозит. Задача. Решение.
1 год это срок вклада. Это важное число,
так как в договоре о вкладе может быть указано, что
если вкладчик изымет сумму вклада до истечения срока (в нашем случае 1 год), то вкладчик потеряет процент.Это может случится если вкладчику срочно понадобились денежные средства (не важно зачем).
В таком случае вкладчику выгоднее потерять проценты, но иметь возможность вернуть первоначальную сумму.
Слайд 9Депозит. Задача. Решение.
Последовательность решения:
Сколько будет 10% от 100000 рублей?
Ответ: 100000*10%/100%
= 10000 рублей.
Сколько будет денег на счете вкладчика через 1
год?Ответ: 100000 (начальная сумма) + 10000 (проценты) = 110000 рублей.
Можно ли сделать расчет быстрее? Да!
Слайд 10Депозит. Задача. Решение.
Распишем решение вынеся 100000 за скобки:
Было: 100000 +
100000*0,1
Стало: 100000*(1+0,1) = 110000 рублей, где
0,1 это представление процентов
как доли, т.е. 10%/100% = 0,1.Получилась задача в одно логическое действие.
Давайте попробуем решить еще одну задачу.
Слайд 11Депозит. Задача 2.
Условие и решение.
Вкладчик положил в банк 200 000
рублей под 5% годовых на 1 год.
Сколько денег будет на
счете вкладчика через 1 год?Решение:
200000*(1+0,05) = 210000 рублей.
Из них 200000 руб. это первоначальная сумма, а
10000 руб. это проценты по вкладу.
Слайд 12Деньги сегодня и завтра
Вопрос: что вы предпочтете - 100 рублей
сегодня или 110 рублей через 1 год если известно, что
любой банк дает 5% годовых дохода по депозиту?Ответ: всегда лучше «синица в руках, чем журавль в небе», поэтому мы возьмем 100 рублей сегодня.
Правильно?
Нет, неправильно!
сейчас
через год
Слайд 13Деньги сегодня и завтра
Давайте применим знания о процентах по депозитам
и разберемся.
Итак, 100 рублей под 5% годовых дадут нам через
1 год – 100*(1+0,05) = 105 рублей.Что же получается?! Если мы примем предложение взять 100 рублей сегодня, то через 1 год у нас будет только 105 рублей, а не 110 рублей как могло бы быть, если бы мы приняли второй вариант!
Слайд 14Деньги сегодня и завтра
Самое интересное, что можно сделать расчет и
в обратную сторону. Это как же?
Сколько денег нужно положить в
банк сейчас под 5% годовых, чтобы через 1 год получить 110 рублей?Т.е. Х*(1+0,05) = 110 рублей. Осталось найти Х, что мы умеем делать давно!
Х = 110/1,05 = 104,76 рублей.
Т.е. в сегодняшних деньгах 110 рублей через 1 год при 5% ставке депозита будут равны 104 рублям и 76 копейкам!
Слайд 15Деньги сегодня и завтра
Вот так мы и познакомились с двумя
понятиями из современных финансов: настоящей и будущей стоимостью. В мировой
практике их чаще всего обозначают устоявшимися английскими сокращениями:PV – present value (настоящая стоимость).
FV – future value (будущая стоимость).
Что же в нашем примере было PV, а что же было FV?
Слайд 16Деньги сегодня и завтра
PV – present value (настоящая стоимость) это
были 100 рублей и 104,76 рублей.
FV – future value (будущая
стоимость) это были 105 рублей и 110 рублей.Простой вывод из наших рассуждений: сравнивать можно любые показатели отнесенные к одному времени! Т.е. нельзя без расчета знать что больше: 100 рублей сегодня или 110 рублей завтра! Надо сделать расчет и привести все данные задачи или к настоящим (PV) или к будущим (FV) величинам.
Слайд 17Так уж ли сложен «сложный процент»?
Давайте усложним первоначальное условие задачи.
Давайте положим 100000 рублей под 10% годовых, но не на
1 год, а на целых 3 года. Что изменится?Важная мысль условия задачи - процент по вкладу начисляется один раз в год, в конце каждого года!
Давайте рассчитаем сколько будет денег на вкладе через 3 года.
Слайд 18Так уж ли сложен «сложный процент»?
Через 1 год на вкладе
будет:
100000*(1+0,1) = 110000 рублей.
Через еще 1 год, т.е. всего через
2 года будет:110000*(1+0,1) = 121000 рублей.
Через еще 1 год, т.е. всего через 3 года будет:
121000*(1+0,1) = 133100 рублей.
Как будто мы забираем вклад и проценты через каждый прошедший год и сразу кладем еще на 1 год, причем кладем не только первоначальную сумму, но и сумму накопленных процентов.
Слайд 19Так уж ли сложен «сложный процент»?
Обратите внимание, что сумма процентов
возрастает, так как после 1 года проценты начинают начисляться на
проценты предыдущих лет. Если бы это было не так, то каждый год бы добавлялось по 10000 рублей и через 3 года сумма составила всего 130000 рублей, а не 133100 рублей. Это и есть эффект «сложного процента».Вопрос: можно ли упростить расчет, особенно если лет будет много или, например, банк платит проценты 1 раз в месяц, т.е. даже за один год надо будет считать проценты 12 раз?
Ответ: да, конечно! Давайте разберемся.
Слайд 20Так уж ли сложен «сложный процент»?
Наш расчет был:
Через 1 год
на вкладе будет:
100000*(1+0,1) = 110000 рублей.
Через еще 1 год, т.е.
всего через 2 года будет:110000*(1+0,1) = 121000 рублей.
Через еще 1 год, т.е. всего через 3 года будет:
121000*(1+0,1) = 133100 рублей.
Слайд 21Так уж ли сложен «сложный процент»?
Давайте подставим каждое предыдущее вычисление
в последующее:
100000*(1+0,1)*(1+0,1)*(1+0,1) = 133100 рублей.
...или…
100000*(1+0,1)3 = 133100 рублей.
…или…
В общем виде:
PV*(1+r)n = FV, гдеPV – настоящая стоимость,
r – процентная ставка,
n – количество периодов начисления процентов,
FV – будущая стоимость.
Слайд 22Так уж ли сложен «сложный процент»?
Мы почти «забыли» про «сложный
процент».
Где же он? А он равен проценту, который мы
получили с учетом того, что проценты начислялись на проценты.В нашем случае: 100000*(1+0,1)3 = 133100 рублей.
Сложный процент равен: (1+0,1)3 – 1 = 0,331 или 33,1%. Но это ведь за 3 года! А сколько будет в пересчете на 1 год?
0,331/3 = 0,11333 или 11,33% годовых (простых %).
Слайд 23Так уж ли сложен «сложный процент»?
Давайте теперь усложним задачу со
сложным процентом!
Воспользуемся формулой:
PV*(1+r)n = FV
чтобы найти сумму на вкладе
через 20 лет. Сложно? Нет, очень просто!100000*(1+0,1)20 = 672750 рублей!
Компьютер в банке сделает возведение в 20 степень в считанные доли секунды, но, главное, теперь мы знаем как он считает!
Слайд 24Давайте попрактикуемся
Найдите сколько будет денег на вашем вкладе в банке,
если вы положили 10000 рублей под столько процентов годовых, каков
ваш номер в классном журнале, на столько лет, каков номер в классном журнале вашего соседа по парте.На решение дается 5 минут.
Пользоваться калькулятором можно!
Слайд 25Кредит
Кредит - это передача во временное пользование оговоренного количества денег
от кредитора заемщику за плату в виде кредитного процента.
Слайд 26Научимся считать сколько денег мы будем должны кредитору при определенных
условиях кредитования
Слайд 27Кредит. Задача. Условие.
Заемщик взял в банке 10000 рублей под 10%
годовых на 1 год.
Сколько денег заемщик должен вернуть банку
через 1 год?Не похожа ли данная задача на ту, что мы решали про депозиты?
Вроде похожа, но не сразу понятно как!
Давайте разберемся!
Слайд 28Кредит. Задача. Условие.
Давайте вспомним нашу старую задачу про депозит (вклад
в банке).
Вкладчик положил в банк 100 000 рублей под 10%
годовых на 1 год. Сколько денег будет на счете вкладчика через 1 год?А теперь перепишем ее немного другими словами.
Банк взял в долг у вкладчика 100 000 рублей под 10% годовых на 1 год. Сколько банк будет должен вернуть вкладчику через 1 год?
Получилось, что задача про депозит и про кредит абсолютно одинаковые задачи! Ура!!! Давайте же её решим.
Слайд 29Кредит. Задача. Решение.
Заемщик взял в банке 10000 рублей под 10%
годовых на 1 год. Сколько денег заемщик должен вернуть банку
через 1 год?10000*(1+0,1) = 11000 рублей.
Формально всё правильно, но в реальности банк не будет ждать целый год, чтобы взять с заемщика процент. Он будет брать процент каждый месяц в течение года.
Но тогда у нас появляется новая задача. Сформулируем её.
Слайд 30Кредит. Задача 2. Условие. Решение.
Заемщик взял в банке 10000 рублей
под 12% годовых на 1 год. Процент начисляется ежемесячно равномерно.
Сколько денег заемщик должен вернуть банку через 1 год?Теперь мы сначала должны найти ежемесячный процент. Тут всё просто. Это 12% разделить на 12 месяцев. Т.е. 1% в месяц.
Давайте сначала решим задачу как будто заемщик не возвращает долг в течение месяца (что ему совсем невыгодно) и возвращает всю сумму и все проценты в конце срока, т.е. через 12 месяцев.
10000*(1+0,01)12 = 11268,25 рублей.
Слайд 31Кредит. Задача 2. Условие. Решение.
И мы опять наблюдаем действие сложных
процентов, так как если бы простые проценты просуммировать 12 раз
получилось бы 11200 рублей долга. 68,25 рублей «набежали» за счет сложных процентов.Расчет теперь верный, но ситуация опять не совсем реалистичная. Ведь любой банк будет хотеть получать проценты по мере их начисления, а любой заемщик будет стремиться быстрее погасить кредит, чтобы избежать переплаты процентов.
Слайд 32Кредит. Задача 3. Условие.
Заемщик взял в банке 1000000 рублей под
10% годовых на 3 года. Процент начисляется ежегодно. Кредит и
процент погашаются тремя одинаковыми платежами сразу после начисления процентов. Составьте расписание погашения данного кредита.Решение данной стандартной кредитной задачи требует знакомства с еще один понятием из мира финансовой математики – аннуитета.
Мы не будет углубляться в данное понятие в рамках школьного предмета, но общее представление дадим.
Слайд 33Аннуитет
Аннуитет это погашение кредита равномерными (одинаковыми) платежами так, что сумма
всех платежей будет равна размеру основного долга и сумме всех
причитающихся банку (кредитору) процентов.Формула вычисления аннуитетного платежа выводится из знания рядов из курса математики. Мы не будем останавливаться на том как вывести формулу, мы рассмотрим ее смысл и применимость для решения задач.
Слайд 34Аннуитет. Формула.
Приведем формулу для так называемого коэффициента аннуитета. Точнее –
коэффициента настоящей стоимости будущих аннуитетных платежей.
PVIFAr,n = 1/r – 1/(r(1+r)n
Все
компоненты формулы мы уже знаем, а именно:r – процентная ставка,
n – количество периодов начисления процентов.
Осталось узнать чему равен аннуитетный платеж банку.
Платеж = (Размер долга) / PVIFAr,n
Слайд 35Кредит. Задача 3. Решение.
Напомним условие задачи.
Заемщик взял в банке 1000000
рублей под 10% годовых на 3 года. Процент начисляется ежегодно.
Кредит и процент погашаются тремя одинаковыми платежами сразу после начисления процентов. Составьте расписание погашения данного кредита.Найдем коэффициент PVIFAr,n = 1/r – 1/(r(1+r)n:
PVIFAr,n = 1/0,1 – 1/(0,1(1+0,1)3 = 2,486851991.
Найдем ежегодный платеж:
Платеж = 1000000 / 2,486851991 = 402114,80 рублей.
Слайд 36Кредит. Задача 3. Решение.
Теперь у нас есть все необходимые данные,
чтобы составить расписание погашения кредита.
Принято составлять таблицу с 5 столбцами,
назовем их буквами латинского алфавита:A – номер периода, где 0 это период взятия кредита и никакого погашения еще не происходит.
B – ежегодный одинаковый платеж. Его мы уже рассчитали по формуле аннуитета.
Слайд 37Кредит. Задача 3. Решение.
C – процент по кредиту начисляется на
остаток кредита. Т.е. в первом случае на весь кредит в
1 млн. рублей, а потом на всё меньшую сумму.D – показывает сколько денег из платежа пошло на уплату основного долга, т.е. на сколько уменьшился долг. Это разница платежа и процента за этот период.
F – остаток долга по кредиту. В период 0 он равен сумме кредита, а в период 3 после уплаты последнего платежа он должен стать равным нулю.
Слайд 41Найдем сколько в первый год мы выплатили основного долга. Вычтем
100000 из 402114,80. запишем в D.
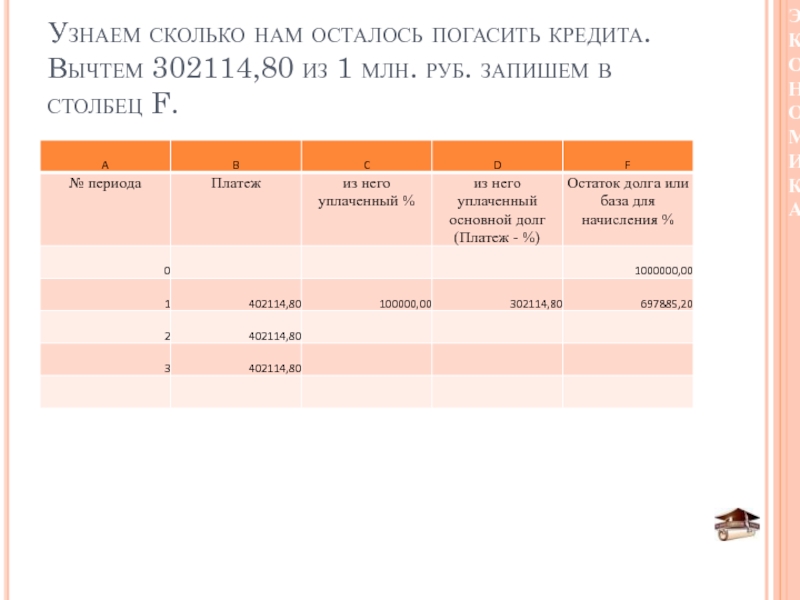
Слайд 42Узнаем сколько нам осталось погасить кредита. Вычтем 302114,80 из 1
млн. руб. запишем в столбец F.
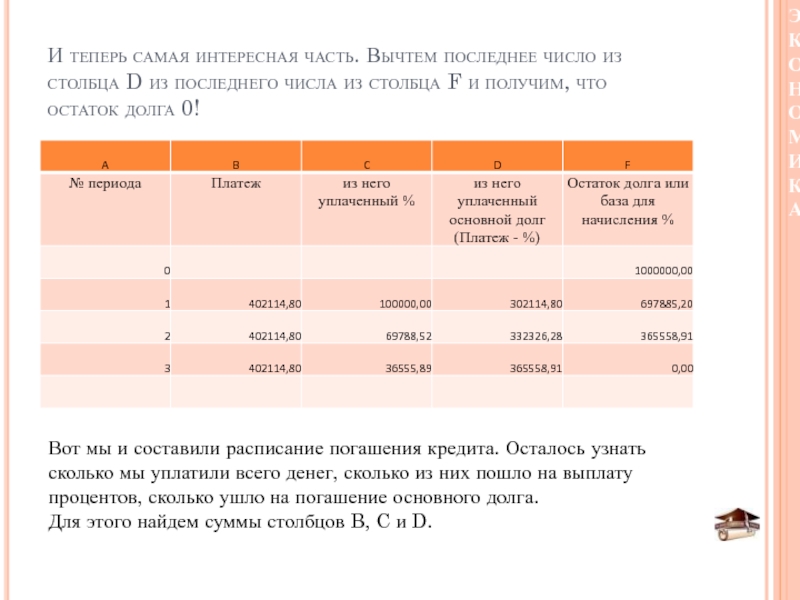
Слайд 48И теперь самая интересная часть. Вычтем последнее число из столбца
D из последнего числа из столбца F и получим, что
остаток долга 0!Вот мы и составили расписание погашения кредита. Осталось узнать сколько мы уплатили всего денег, сколько из них пошло на выплату процентов, сколько ушло на погашение основного долга.
Для этого найдем суммы столбцов B, C и D.
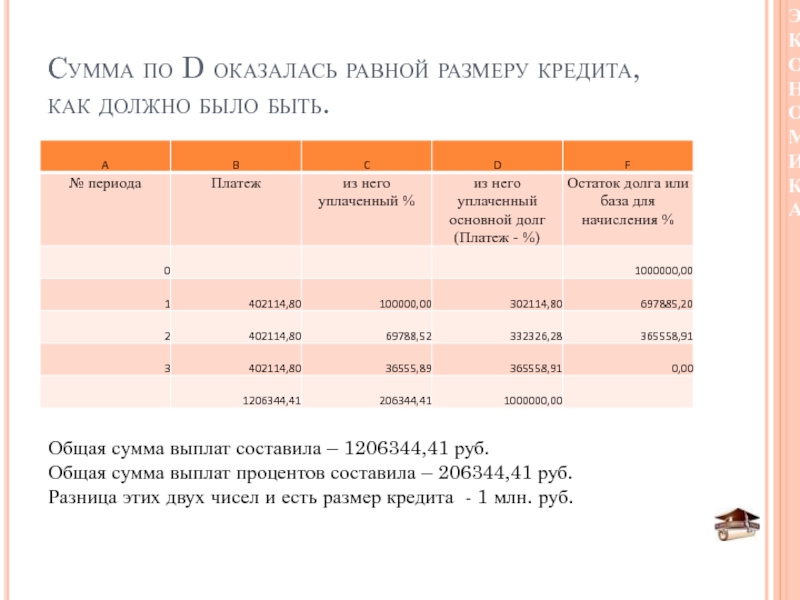
Слайд 49Сумма по D оказалась равной размеру кредита, как должно было
быть.
Общая сумма выплат составила – 1206344,41 руб.
Общая сумма выплат процентов
составила – 206344,41 руб.Разница этих двух чисел и есть размер кредита - 1 млн. руб.
Слайд 50Задание на уроке
Составить расписание погашения кредита если размер кредита 3
млн. руб. Срок 5 лет. Процент по кредиту равен вашему
номеру в классном журнале. Погашение ведется равными платежами в конце каждого года сразу после начисления процентов за прошедший год.Самопроверка: если в последнем столбце в последней строке получилось «0», значит вы нигде не ошиблись!
Слайд 53список использованных печатных источников
1. Экономика. (Основы экономической теории): Учебник для
10-11 классов общеобразоват. орг. Углубленный уровень образования. / Под ред.
С.И. Иванова, А.Я. Линькова – 22-е изд. В 2-х книгах М.: ВИТА-ПРЕСС, 2016.2. Деньги, кредит, банки : учебник и практикум для академического бакалавриата / под ред. Н.Н. Мартыненко, Ю.А. Соколова. – М.: Издательство Юрайт, 2017.
Слайд 54активные ссылки на страницы материалов в Интернете
Статья «Что такое
кредит? Виды кредитов»
http://www.banki.ru/wikibank/kredit/
Статья «Депозит»
http://www.banki.ru/wikibank/depozit/
Статья «Процентные ставки по вкладам»
http://www.banki.ru/wikibank/protsentnyie_stavki_po_vkladam/
Статья «Аннуитет. Аннуитетные
платежи»
https://finances-analysis.ru/procent/annuity.htmСлайд 55активные ссылки на использованные изображения
Изображение «восклицательного знака»: http://hispablog.ru/wp-content/uploads/2013/12/signos-e1408254691590.jpg
Изображение «вопросительного
знака»: http://hispablog.ru/wp-content/uploads/2013/12/signos-e1408254691590.jpg
Изображение смайлика «всё супер»: https://pp.userapi.com/c629307/v629307865/14c60/mPaa0-HqRT4.jpg
Изображение «банка»: http://chellombard.ru/wp-content/uploads/2016/06/bank-dengi-pod-zalog-pts.gif
Изображение «стопки денег
маленькой»: https://img-fotki.yandex.ru/get/15495/200418627.59/0_117a94_2af3dbf6_orig.pngИзображение «стопки денег большой»: https://img-fotki.yandex.ru/get/15495/200418627.59/0_117a94_2af3dbf6_orig.png
Изображение «знака процента»: http://4udesnaya-da4a.com/wp-content/uploads/percent.jpg
Изображение «знака равно»: https://pixabay.com/p-150803
Изображение «знака плюс»: http://rkamen.pnzreg.ru/files/kamenka_pnzreg_ru/2013/03/plus-.jpg
Изображение «мыслителя»: https://pp.userapi.com/c4303/g28379894/a_739e8082.jpg
Изображение «1 год»: http://nevafootball.ru/wp-content/uploads/2015/03/Untitled-1.png
Изображение «девочка с плакатом «Ура!»: https://img-fotki.yandex.ru/get/6433/58581001.97/0_a4e67_9f97b1bf_S